Лабораторная работа 3
При создании использовалась монография «Тестирование учебных достижений» В.С. КИМ http://uss.dvfu.ru/static/kim_testing_monograph/index.html
(в некоторых расчетах приведены приблизительные значения)
1. Проверить тест на надежность, используя различные подходы
А) рассчитав коэффициент надежности для двукратного тестирования
(матрицу повторного тестирования получить самостоятельно из первоначальной изменив случайно некоторые значения).
Работаем на новом листе, скопируем нашу матрицу. Продублируем матрицу, чтобы у нас было две матрицы на листе.
И изменим случайно некоторые значения. Допустим единицу (2х4) на ноль. Ноль (8х13) на единицу и т.д. Не более четырех всего.
Затем посчитаем корреляцию между Xi первой матрицы и Xi второй. Функция «КОРРЕЛ», первый массив – столбик Xi для первой матрицы, а второй массив соответственно Xi второй матрицы. У нас получилось значение = 0,962. Сделаем выводы. У нас хорошая корреляция, значит, тест обладает высокой надежностью.
Тест можно использовать, если его коэффициент надежности не менее +0,7.
Б) метод расщепления на четные и нечетные задания, для коррекции использовать формулу Спирмена-Брауна
Используем только первую матрицу. Считаем баллы по четным и нечетным заданиям.
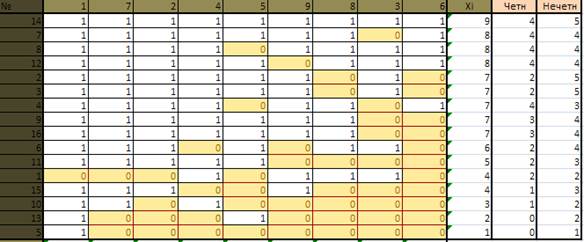
Считаем корреляцию, где массив 1 это столбик Четн, а массив 2 соответственно Нечетн.
Наша корреляция равна 0,64. Поскольку для определения надежности использовалась лишь половина теста, то полученное значение rt (наш коэффициент надежности) является заниженным. Для коррекции значения rt используется формула Спирмена-Брауна, где rt’ – исправленный коэффициент надежности; rt – коэффициент надежности по половинкам расщепленного теста.
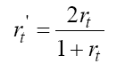
В нашем случае получается, исправленный коэффициент = 2*0,64/(1+0,64) = 0,78.
Исправленное значение показывает удовлетворительную надежность теста (больше +0,7).
 2015-05-10
2015-05-10 1995
1995







