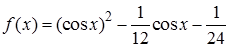Фрагмент решения задачи 2.1.0

=0, [a,b]=[0, ]

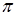Аналитическое решение задачи:

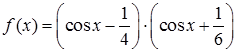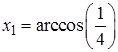, =1.31811607652818, 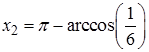=1.738244406014586

Численное решение задачи: Локализация корней для численного решения задачи:

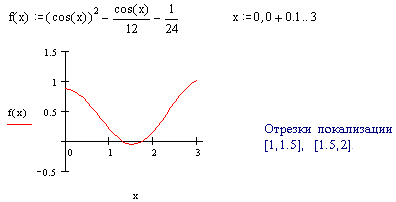
Метод бисекции

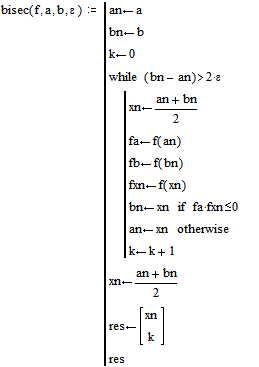
ПЕРВЫЙ КОРЕНЬ

bisec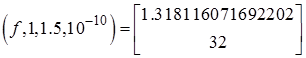

Встроенная функция пакета MATHCAD

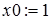- задание начального приближения

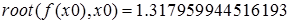
Значение корня отличается от найденного с помощью функции bisec, так как по умолчанию величина погрешности при работе встроенных функций равна 0.001.

Переопределим параметр для задания погрешности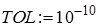

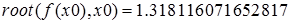
Значение корня с заданной точностью 1.3181160717.

ВТОРОЙ КОРЕНЬ

bisec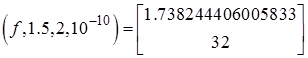

Значение корня с заданной точностью 1.7382444060, число итераций 32.

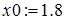- задание начального приближения

.

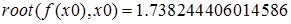Значения корней в пределах заданной точности совпадают.

ПРИЛОЖЕНИЕ 2.C

Расчетные формулы методов решения нелинейного уравнения .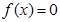

Упрощенный метод Ньютона: 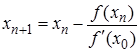, n=0,1,…

Метод ложного положения: 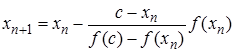, n=0,1,…;

c-фиксированная точка из окрестности корня

Метод секущих: 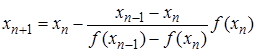, n=0,1,…

Метод Стеффенсена: 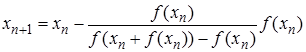, n=0,1,…

Модифицированный метод Ньютона для поиска кратных корней:

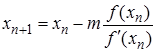, n=0,1,…, m=1,2,…

* Расчетная формула модификации метода Ньютона для поиска кратных корней дана в ПРИЛОЖЕНИИ 2.C.

** Расчетные формулы упрощенного метода Ньютона и метода секущих даны в ПРИЛОЖЕНИИ 2.C.