Порядок выполнения работы. 1. Структурная схема системы третьего порядка, состоящей из трех звеньев первого порядка приведена на рис.2

1. Структурная схема системы третьего порядка, состоящей из трех звеньев первого порядка приведена на рис.2

Передаточная функция данной разомкнутой системы равна

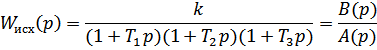
2. Запишите передаточную функцию замкнутой системы с единичной отрицательной связью ,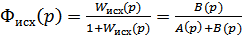

где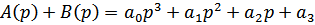

a₀ = T₁T₂T₃=0.2 a₁ = T₁T₂ + T₁T₃ + T₂T₃=1.4 a₂ = T₁ + T₂ + T₃=2.2 a₃= 1 + b₀=16

b₀ = k₁k₂k₃ =k=15 (не устойчиво,берём k=10 => a₃=11)

Таблица 1

Вариант	K	Т1	Т2	Т3	Т4	Т5
				0,2		0,2

3. В соответствии с заданным вариантом из таблицы 1, рассчитайте коэффициенты полиномов числителя B(p) и знаменателя A(p) + B(p) передаточной функции исходной замкнутой системы Ф_исх(p).

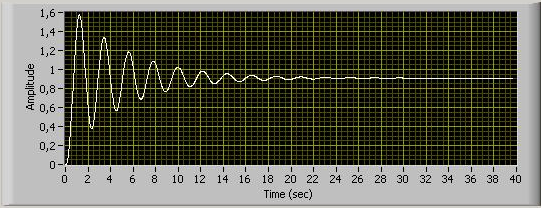
Введите с клавиатуры ПК полученные данные в выражение для передаточной функции замкнутой системы и получите переходную характеристику h(t).

Определите по полученной осциллограмме прямые показатели качества переходного процесса:

- статическую ошибку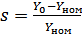

- время регулирования t_р – 14,5 сек

- перерегулирование 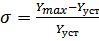= 77%

4. Введите в состав САУ последовательно интегро-дифференцирующее звено с передаточной функцией W_кз(p)

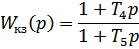
Результирующая передаточная функция скорректированной замкнутой САУ при этом будет равна 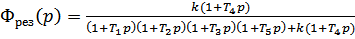где

a₀ = T₁T₂T₃T₅=0 a₁ = T₁T₂T₃ + T₁T₂T₅ + T₂T₃T₅ + T₁T₃T₅=0.2

a₂ = T₁T₂ + T₁T₃ + T₁T₅ + T₂T₃ + T₂T₅ + T₃T₅ =1.4 a₃ = T₁ + T₂ + T₃ + T₅ + k T₄=17.2

a₄= 1 + k=16

T₃=0

Рассчитайте новые значения коэффициентов полиномов числителя B(p) и знаменателя A(p) + B(p) передаточной функции скорректированной замкнутой системы Ф_рез(p).

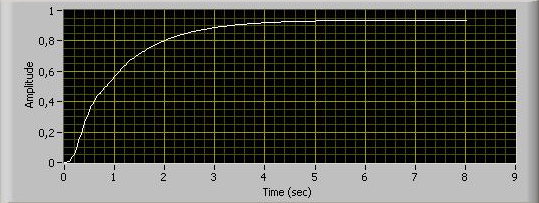
Введите с клавиатуры ПК полученные данные в выражение для передаточной функции замкнутой системы и получите переходную характеристику h(t).

Определите по полученной осциллограмме прямые показатели качества переходного процесса:

- статическую ошибку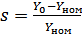

- время регулирования t_р=3.4

- перерегулирование 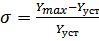=0

5. По передаточным функциям исходной САУ и корректирующего звена построить логарифмические амплитудные и фазовые характеристики исходной разомкнутой САУ, корректирующего звена и скорректированной системы.