Синтаксис функции «БЗ»

БЗ(<процентная ставка>;<количество периодов>;<выплата>;[<начальное значение>];[<тип>]) – возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

<тип> – определяет время начисления процентов: в конце/начале (0/1) периода. Если тип пропущен, он считается равным 0.

è Ввести в ячейку В5 функцию БЗ. В открывшееся диалоговое окно мастера функций ввести исходные данные (см.рис.54)

Теперь рабочий лист подготовлен для применения команды: ØСервис ØПодбор параметра… (внешний вид – рис.55).

Этап №2. Применение команды ØСервис ØПодбор параметра...

è Из меню Сервис выбрать команду Подбор параметра…. Откроется окно, представленное на рис.56.

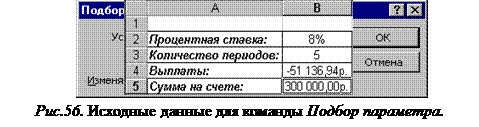èВ окне Подбор параметра задать исходные данные согласно рис. 56, затем нажать Ok. Внешний вид рабочего листа после итерационных вычислений представлен на рис 57.

Рис.57

Пример 2. Отыскать корень алгебраического уравнения: (2x²+3)*(1- sin(x)) = ln(x) +2.

Замечание: Для того чтобы найти корень уравнения, нужно подобрать такое значение х, прикотором значение выражения (2x²+3)*(1 – sin(x)) – ln(x) – 2 равно нулю. При решении таких задач важно, чтобы корень действительно существовал.

Этап №1. Подготовительный.

è Ячейке А1 присвоить имя х, используя команду ØВставка ØИмя ØПрисвоить…

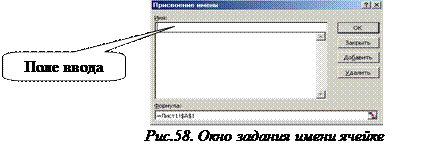
В открывшемся окне «Присвоение имени» в поле ввода ввести х и нажать ОК.

èВ ячейку В1 ввести формулу преобразованного уравнения, которое получено путем переноса всех его элементов в одну часть:

= (2*x^2+3)*(1 – sin(x)) – ln(x) – 2

è В ячейку А1 ввести любое число (оно буден являться начальным значением изменяемого параметра), учитывая область определения функции f(x)= (2x²+3)*(1- sin(x)) – ln(x) +2, например 1.

èВ ячейке В1 автоматически будет вычислено значение функции f(x) при х=1.

Этап №2. Применение команды «Подбор параметра...»

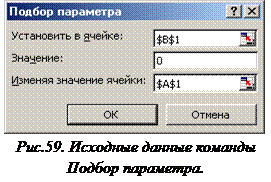
è Выполнить команду Ø Сервис Ø Подбор параметра… В окне Подбор параметра задать исходные данные (см. рис.59). В ячейке А1 в результате итерационных вычислений будет найден корень уравнения.

Пример 3. Имеется многоступенчатое пищевое производство. Относительные нормативные потери на каждом этапе обработки известны из опытных данных и заданы директивно.

• объем продукта на выходе должен быть 800 кг;
• количество этапов обработки – 3;
• коэффициенты нормативных потерь на каждом этапе от поступившего на данный вид обработки объема продукта: на I этапе коэффициент потерь – 0,05; на II этапе – 0,11; на III этапе – 0,02.

Вычислить:

• объем потерь на каждом этапе обработки;
• необходимое количество исходного продукта.