Задание 1. Найти общее решение системы линейных уравнений, используя пакет Maple.
1 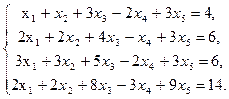 2
2 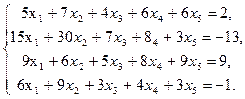
3 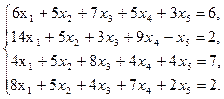 4
4 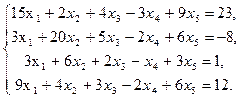
5 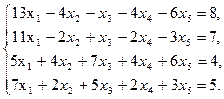 6
6 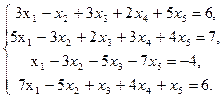
7 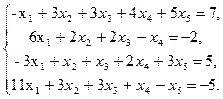 8
8 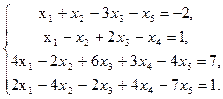
9 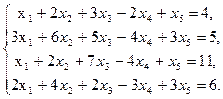 10
10 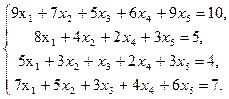
Задание 2. Решить задачу минимизации или максимизации функции с помощью
пакета Maple.
Пример:
Найти максимум функции 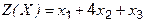 , где переменные
, где переменные 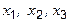 больше или равны нуля и удовлетворяют условиям:
больше или равны нуля и удовлетворяют условиям:
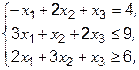
Решение. Максимизация или минимизация функций, удовлетворяющих заданным условиям, выполняется командами maximize или minimize соответственно. Эти команды содержатся в библиотеке simplex, включающем функции линейного программирования.
Итак, сначала необходимо подключить библиотеку с помощью команды:
> with(simplex);
В результате на экран будет выведен список доступных функций пакета.
Далее, можно ввести функцию 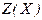 и систему ограничений, накладываемых на значения переменных:
и систему ограничений, накладываемых на значения переменных:
> Z:=2*x1+4*x2;
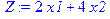
> eq:={-2*x1+3*x2<=12,x1+x2<=9,3*x1-2*x2<=12};
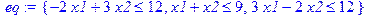
Формат команд максимизации и минимизации аналогичен:
maximize(f, C, vartype)
где f – целевая функция, C – множество ограничений, накладываемых на переменные, vartype – тип переменных (NONNEGATIVE – неотрицательные, UNRESTRICTED – могут принимать любые значения). Тогда, для вывода решения необходимо ввести команду:
> maximize(Z,eq,NONNEGATIVE);
Получен результат:
Программа выведет результат, если решение существует, и значение NULL в противном случае.
| Вариант | Задача | Вариант | Задача | |
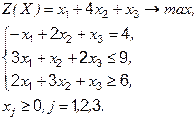 | 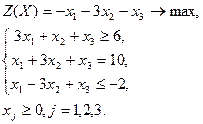 | |||
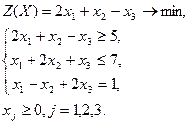 | 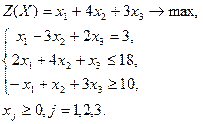 | |||
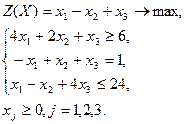 | 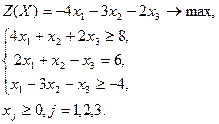 | |||
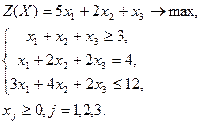 | 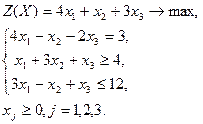 | |||
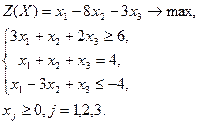 | 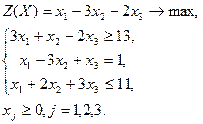 |
Задание 3. Построить математическую модель транспортной задачи (по критерию стоимости) в пакете Maple и решить ее с помощью функции minimize(). Вывести значение целевой функции на экран, если решение существует.
Пример. Пусть даны исходные данные задачи:
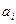  | |||
Решение. 1) Математическая модель задачи примет вид:
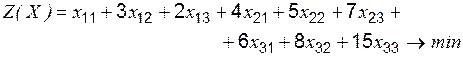 - целевая функция;
- целевая функция;
Система ограничений: расход всех запасов не должен превышать их количества, запросы должны быть удовлетворены:
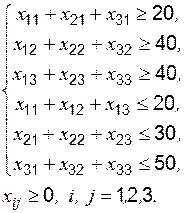
2) Введем матрицу стоимостей с помощью команды matrix в программу:
> C:=matrix(3,3,[[1,3,2],[4,5,7],[6,8,15]]);
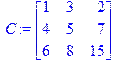
Здесь первый аргумент – число строк, второй – число столбцов, далее в квадратных скобках указаны значения элементов: списки элементов строк также взяты в скобки.
Доступ к элементу матрицы осуществляется в формате: имя матрицы (номер строки, номер столбца). Например:
> C[2,3];
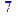
3) Объявим матрицу неизвестных: количество перевозимого груза (команда print используется для вывода результат на экран):
> X:=matrix(3,3):print(X);
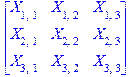
4) Введем матрицу запросов (в виде строки):
> B:=matrix(1,3,[20,40,40]);
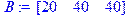
5) Введем матрицу запасов (в виде столбца):
> A:=matrix(3,1,[20,30,50]);
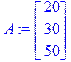
6) Для того, чтобы ввести ограничения, сделаем несколько вспомогательных действий.
Подключим библиотеку, содержащую функции линейной алгебры:
> with(linalg):
Введем строку, содержащую единицы, число которых совпадает с количеством поставщиков:
> E1:=matrix(1,3,[1,1,1]);
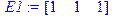
Умножим эту строку на матрицу X:
> Y1:=(multiply(E1,X));
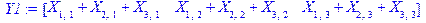
Введем строку, содержащую единицы, число которых совпадает с количеством потребителей (если число поставщиков и потребителей одинаково, можно использовать E1):
> E2:=matrix(1,3,[1,1,1]);
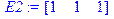
Транспонируем матрицу X и умножим результат на E2:
> X1:=transpose(X);Y2:=(multiply(E2,X1));
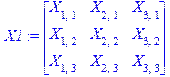
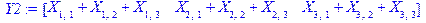
Введем ограничения, соответствующие математической модели:
> eq:={Y1[1]>=B[1,1],Y1[2]>=B[1,2],Y1[3]>=B[1,3],
Y2[1]<=A[1,1],Y2[2]<=A[2,1],Y2[3]<=A[3,1]};
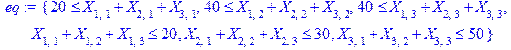
7) Для ввода целевой функции, воспользуемся операцией строки матрицы C на столбец матрицы Х. Функции row (C, i) и col (C, j) извлекают строку i и столбец j из матрицы С соответственно:
> Z:=multiply(row(C,1),col(X1,1))+
multiply(row(C,2),col(X1,2))+multiply(row(C,3),col(X1,3));
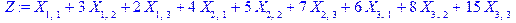
8) Подключим библиотеку simplex:
> with(simplex):
9) Найдем значения переменных гарантирующие минимум целевой функции с учетом ограничений:
> Z1:=minimize(Z,eq, NONNEGATIVE);
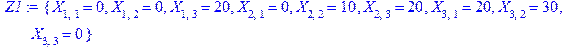
10) Реализуем присвоение найденных значений переменных матрице Х с помощью команды assign и выведем на экран решение и значение целевой функции:
> Z1:=assign(Z1):print(X);Z;
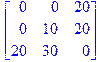
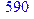
Варианты задания
1.
| 2.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.
| 4.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5.
| 6.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.
| 8.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9.
| 10.
|
Задание 4. Автомобильный завод выпускает микроавтобусы, грузовики и внедорожники, используя общий склад комплектующих деталей и узлов. С учетом ограниченности запаса комплектующих необходимо найти оптимальное соотношение объемов выпуска изделий, при котором прибыль от реализации будет максимальной. Следует учитывать уменьшение удельной прибыли при увеличении объемов производства в связи с дополнительными затратами на сбыт. Численные значения норм расхода и складские запасы комплектующих, а также цен на готовую продукцию взять из таблицы.
Пример. Обозначим за 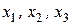 искомые объемы производства микроавтобусов, грузовиков и внедорожников (переменные, по которым будем проводить оптимизацию), тогда целевая функция с учетом дополнительных затрат на сбыт примет вид:
искомые объемы производства микроавтобусов, грузовиков и внедорожников (переменные, по которым будем проводить оптимизацию), тогда целевая функция с учетом дополнительных затрат на сбыт примет вид:

Для складских запасов справедливы следующие соотношения:
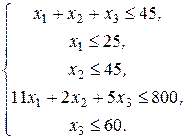
Задача решается аналогично транспортной задаче.
Численные значения норм расхода и складские запасы комплектующих,
цены на готовую продукцию
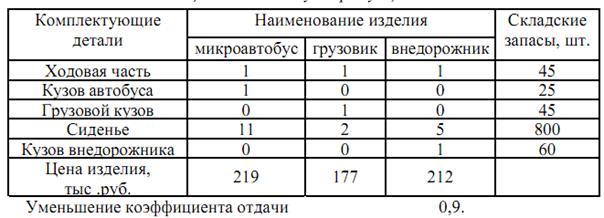
Варианты задания
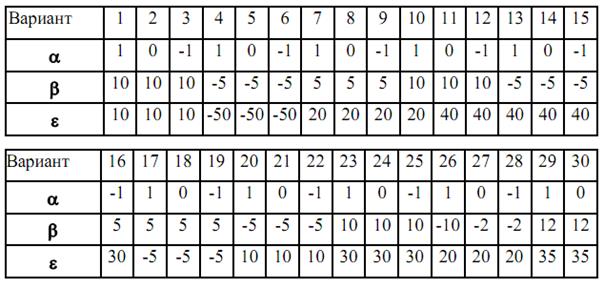
Исходные данные по вариантам заданы в таблице 1. Для изменения численных значений исходных данных в разных вариантах заданий введены параметры 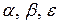 . Значения параметров
. Значения параметров 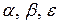 для различных вариантов взять из таблицы 2. Интерпретировать результирующие данные, полученные в результате расчетов.
для различных вариантов взять из таблицы 2. Интерпретировать результирующие данные, полученные в результате расчетов.
Таблица 1
Численные значения норм расхода и складские запасы комплектующих и
цены на готовую продукцию
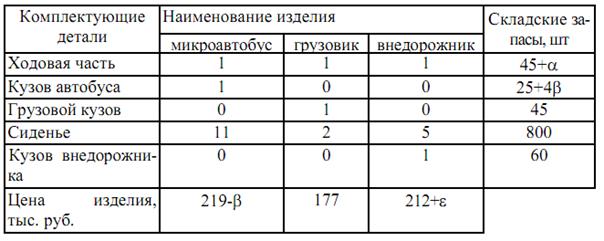
Таблица 2
Варианты к практическому заданию
Задание 5. Фирма выпускает изделия двух видов, А и В. Для выпуска этих изделий используется сырье четырех типов. Расход сырья каждого типа на изготовление единицы продукции и запасы сырья заданы таблицей.
 2015-05-10
2015-05-10 1266
1266