Однородные системы линейных уравнений

Системы линейных уравнений, у которой все свободные члены равны нулю, называются однородными:

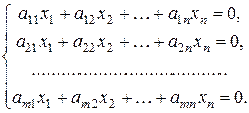
Любая однородная система всегда совместна, поскольку всегда обладает нулевым (тривиальным) решением. Возникает вопрос, при каких условиях однородная система будет иметь нетривиальное решение.

Теорема 5.2. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг основной матрицы меньше числа ее неизвестных.

Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель основной матрицы системы не равен нулю.

Пример 5.6. Определить значения параметра l, при которых система имеет нетривиальные решения, и найти эти решения:

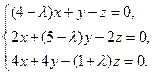
Решение. Эта система будет иметь нетривиальное решение тогда, когда определитель основной матрицы равен нулю:

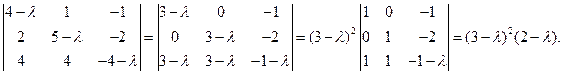
Таким образом, система нетривиальна, когда l=3 или l=2. При l=3 ранг основной матрицы системы равен 1. Тогда оставляя только одно уравнение и полагая, что y = a и z = b, получим x=b–a, т.е.

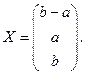
При l=2 ранг основной матрицы системы равен 2. Тогда, выбирая в качестве базисного минор:

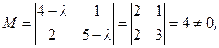
получим упрощенную систему

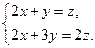
Отсюда находим, что x=z /4, y=z /2. Полагая z =4 a, получим

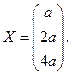à

Множество всех решений однородной системы обладает весьма важным линейным свойством: если столбцы X ₁ и X ₂ – решения однородной системы AX = 0, то всякая их линейная комбинация a X ₁ + b X ₂ также будет решением этой системы. Действительно, поскольку AX ₁ =  0 и AX ₂ =  0, то A (a X ₁ + b X ₂) = a AX ₁ + b AX ₂ = a · 0 + b · 0 = 0. Именно вследствие этого свойства, если линейная система имеет более одного решения, то этих решений будет бесконечно много.

Линейно независимые столбцы E ₁, E ₂, E_k, являющиеся решениями однородной системы, называется фундаментальной системой решений однородной системы линейных уравнений, если общее решение этой системы можно записать в виде линейной комбинации этих столбцов:

.

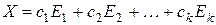Если однородная система имеет n переменных, а ранг основной матрицы системы равен r, то k = n–r.

Пример 5.7. Найти фундаментальную систему решений следующей системы линейных уравнений:

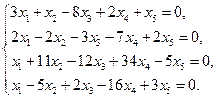
Решение. Найдем ранг основной матрицы системы:

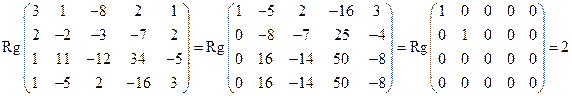
Таким образом, множество решений данной системы уравнений образует линейное подпространство размерности n – r = 5 – 2 = 3. Выберем в качестве базисного минор

.

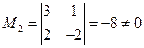Тогда оставляя только базисные уравнения (остальные будут линейной комбинацией этих уравнений) и базисные переменные (осталь­ные, так называемые свободные, переменные переносим вправо), по­лучим упрощенную систему уравнений:

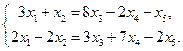
Полагая, x ₃ =  a, x ₄ =  b, x ₅ =  c, находим

, .

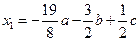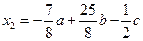Полагая a = 1, b = c = 0, получим первое базисное решение; полагая b = 1, a = c = 0, получим второе базисное решение; полагая c = 1, a = b = 0, получим третье базисное решение. В результате, нормальная фундаментальная система решений примет вид

, , .

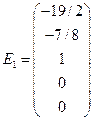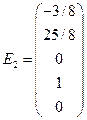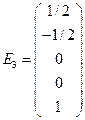С использованием фундаментальной системы общее решение однородной системы можно записать в виде

X = aE ₁ + bE ₂ + cE ₃. à

Отметим некоторые свойства решений неоднородной системы линейных уравнений AX=B и их взаимосвязь соответствующей однородной системой уравнений AX = 0.

Общее решение неоднородной системы равно сумме общего решения соответствующей однородной системы AX = 0 и произвольного частного решения неоднородной системы. Действительно, пусть Y ₀ произвольное частное решение неоднородной системы, т.е. AY ₀ =  B, и Y – общее решение неоднородной системы, т.е. AY = B. Вычитая одно равенство из другого, получим
A (Y–Y ₀) = 0, т.е. Y – Y ₀ есть общее решение соответствующей однородной системы AX =0. Следовательно, Y – Y ₀ =  X, или Y = Y ₀ +  X. Что и требовалось доказать.

Пусть неоднородная система имеет вид AX = B ₁ +  B ₂. Тогда общее решение такой системы можно записать в виде X = X ₁ +  X ₂, где AX ₁ =  B ₁ и AX ₂ =  B ₂. Это свойство выражает универсальное свойство вообще любых линейных систем (алгебраических, дифференциальных, функциональных и т.д.). В физике это свойство называется принципом суперпозиции, в электро- и радиотехнике – принципом наложения. Например, в теории линейных электрических цепей ток в любом контуре может быть получен как алгебраическая сумма токов, вызываемых каждым источником энергии в отдельности.