Идея метода заключается в свёртке целевых функций и поиска минимума вспомогательной функции:
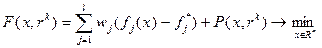 .
.
Задача решается в три этапа:
I этап. Решение оптимизационных задач для каждого из критериев отдельно и получение «идеальной точки» - 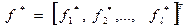 c учетом ограничений.
c учетом ограничений.
II этап. Выбор весовых коэффициентов.
Величины весовых коэффициентов 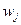 - подбираются исходя из предварительно обусловленных соображений, которые могут быть выражены в виде дополнительных неформализуемых критериев. Чаще всего весовые коэффициенты выбираются путём бинарных сравнений и построения обратно симметричной матрицы. Далее вычисляются собственные значения и для максимального собственного значения выбирается соответствующий собственный вектор, элементы которого используются как весовые коэффициенты (метод Т. Саати). В данном случае весовые коэффициенты могут варьироваться различным образом для исследования пространства эффективных точек.
- подбираются исходя из предварительно обусловленных соображений, которые могут быть выражены в виде дополнительных неформализуемых критериев. Чаще всего весовые коэффициенты выбираются путём бинарных сравнений и построения обратно симметричной матрицы. Далее вычисляются собственные значения и для максимального собственного значения выбирается соответствующий собственный вектор, элементы которого используются как весовые коэффициенты (метод Т. Саати). В данном случае весовые коэффициенты могут варьироваться различным образом для исследования пространства эффективных точек.
III этап. Получение оптимальных по Парето и Слейтеру решений.
Для решения задачи можно использовать методы штрафных функций или метод модифицированных функций Лагранжа.
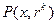 - штрафная функция,
- штрафная функция, 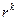 - параметр штрафа, задаваемый на каждой
- параметр штрафа, задаваемый на каждой 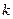 -й итерации. Это связано с возможностью применения эффективных и надежных методов поиска экстремума на основе методов безусловной оптимизации.
-й итерации. Это связано с возможностью применения эффективных и надежных методов поиска экстремума на основе методов безусловной оптимизации.
Штрафные функции конструируются, исходя из следующих условий:
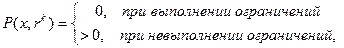
Причем при невыполнении ограничений и 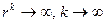 справедливо
справедливо 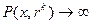 . Чем больше
. Чем больше 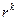 , тем больше штраф за невыполнение ограничений. Как правило, для ограничений типа равенств используется квадратичный штраф, а для ограничений типа неравенств – квадрат срезки:
, тем больше штраф за невыполнение ограничений. Как правило, для ограничений типа равенств используется квадратичный штраф, а для ограничений типа неравенств – квадрат срезки:
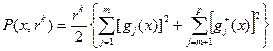 ,
,
где 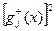 - срезка функции:
- срезка функции:
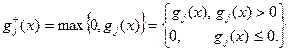

Начальная точка поиска задается обычно вне множества допустимых решений 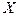 . На каждой
. На каждой 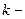 й итерации ищется точка
й итерации ищется точка 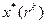 минимума вспомогательной функции
минимума вспомогательной функции 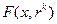 при заданном параметре
при заданном параметре 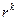 с помощью одного из методов безусловной минимизации. Полученная точка
с помощью одного из методов безусловной минимизации. Полученная точка 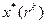 используется в качестве начальной на следующей итерации, выполняемой при возрастающем значении параметра штрафа. При неограниченном возрастании
используется в качестве начальной на следующей итерации, выполняемой при возрастающем значении параметра штрафа. При неограниченном возрастании 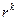 последовательность
последовательность 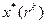 стремится к точке условного минимума
стремится к точке условного минимума 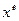 .
.
ЗАДАЧИ
Задача 1. Найти сильно и слабо эффективные решения.
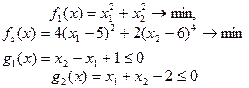
Задача 2. Найти сильно и слабо эффективные решения.
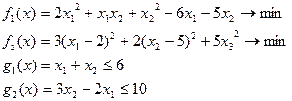
 2015-05-10
2015-05-10 213
213







