2015-05-10
615
ЛАБОРАТОРНАЯ РАБОТА № 4
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Методы свертки критериев (метод «идеальной точки»)
Постановка задачи
Даны дважды непрерывно дифференцируемые целевые функции, представленные в виде вектор-функции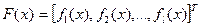 
и функции ограничени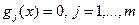й 
и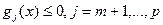 
, определяющие множество допустимых решений 
.
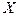Требуется найти недоминируемые (эффективные) решения на множестве 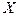, т.е. такое множество решений 
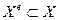, что
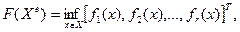
где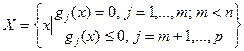 
.
Будем различать сильно эффективные точки (оптимальные по Парето)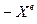 
и слабо эффективные точки (оптимальные по Слейтеру) 
.
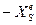Формальное определение сильно эффективных решений (оптимальных по Парето):
,
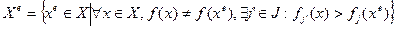т.е. любое допустимое решение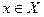 
, отличное по критериям от 
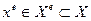(в том числе и другие эффективные точки) хуже выделенного эффективного решения 
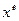хотя бы по одному критерию.
Определение слабо эффективных решений (оптимальных по Слейтеру):
.
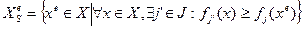Для слабо эффективных решений вместо строго неравенства используется нестрогое и не учитывается условие критериальной нетождественности решений.
Итак, из определений сильно и слабо эффективных решений следует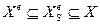 
:
1. каждое допустимое решение (кроме критериально тождественного) хоть в чем-нибудь проигрывает сильно эффективному;
2. каждое допустимое решение хоть в чем-нибудь не выигрывает у слабо эффективного.
