2015-05-10
246
В основе метода лежит закон сохранения энергии:
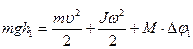(9.13)
где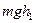 
– потенциальная энергия груза в начальный момент;
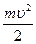– кинетическая энергия груза в нижней точке траектории;
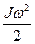– кинетическая энергия маховика, когда груз находится в нижней точке траектории; 
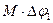– работа по преодолению момента силы трения в подшипниках опоры маховика.
Из уравнения (9.13) необходимо определить момент инерции маховика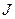 
, выразив его через измеряемые величины.
Величина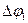 
– угол поворота маховика за время падения груза с высоты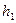 
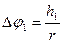. (9.14)
Так как груз движется равноускоренно, то скорость груза в конце движения будет равна
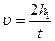. (9.15)
Угловая скорость маховика по определению:
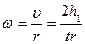. (9.16)
Момент сил трения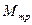 
можно найти следующим образом. После того, как груз достигнет нижней точки, маховик, вращаясь по инерции, поднимет груз на новую высоту 
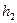, которая меньше .
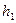Изменение потенциальной энергии груза равно работе против момента сил трения:
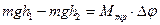, (9.17)
где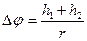 
– угол поворота маховика за время прохождения грузом пути 
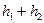. Отсюда момент силы трения в опорах равен:
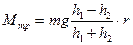. (9.18)
Подставив в выражение (9.13) значения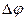 
, 
, 
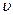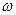и 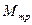из (9.14), (9.15), (9.16) и (9.18) и проделав преобразования, получим выражения для определения момента инерции маховика:
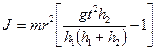. (9.19)
