Задание 1. Найти производные указанных порядков:
f’(x)=axn, f’(x)= sin(x), f’(x,y)= cos(x)y3, f”(x,y)= cos(x)y3,f””(x)=cos(2x)2.
>Diff(a*x^n,x)=diff(a*x^n,x);
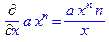
> Diff(sin(x),x)=diff(sin(x),x);
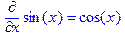
> f(x,y):=cos(x)*y^3;
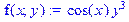
> Diff(f(x,y),x)=diff(f(x,y),x);
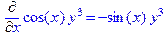
> Diff(f(x,y),x$2,y$2)=diff(f(x,y),x$2,y$2);
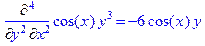
> Diff(sin(x^2),x)=diff(sin(x^2),x);
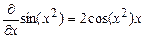
> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);
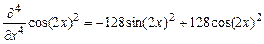
Полученное выражение можно упростить двумя способами:
> simplify(%);
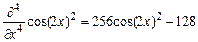
> combine(%);
Задание 2. Вычислить вторую производную функции f(x)=sin2(x)/(2+sin(x)) в точках x =p/2, x =p.
> y:=sin(x)^2/(2+sin(x)): d2:=diff(y,x$2):
> x:=Pi; d2y(x)=d2;
x:=p d2y(p)=1
> x:=Pi/2;d2y(x)=d2;
х:= 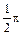
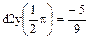
Задание 3. Найти значения определенных интегралов
а) 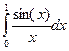 ,
,  б)
б) 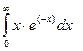 .
.
>Int(sin(x)/x,x=0..1.)=evalf(int(sin(x)/x, x=0..1),3);
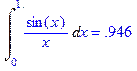
>Int(x*exp(-x),x=0..infinity) = evalf(int(x*exp(-x), x=0..infinity),1);
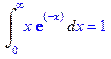
Задание 4. Найти неопределенные интегралы:
а) 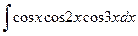 ; б)
; б) 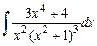 .
.
>Int(cos(x)*cos(2*x)*cos(3*x),x)=int(cos(x)* cos(2*x)*cos(3*x),x);
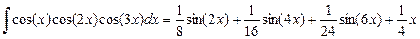
>Int((3*x^4+4)/(x^2*(x^2+1)^3),x)=int((3*x^4+4)/ (x^2*(x^2+1)^3),x);
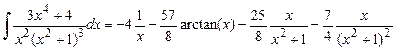
Задание 5. Найти определенный интеграл
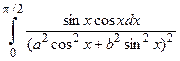 , при условии a >0, b >0.
, при условии a >0, b >0.
> assume (a>0); assume (b>0);
> Int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2),
x=0..Pi/2)=int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*
sin(x)^2),x=0..Pi/2);
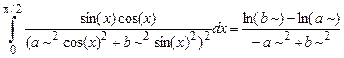
и несобственный интеграл 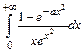 , при условии a >-1.
, при условии a >-1.
> assume(a>-1);
>Int((1-exp(-a*x^2))/(x*exp(x^2)),x=0..+infinity) =int((1-exp(-a*x^2))/(x*exp(x^2)), x=0..+infinity);
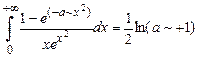
Задание 6. Найти общее решение дифференциального уравнения y '+ y cos x =sin x cos x.
> restart;
> de:=diff(y(x),x)+y(x)*cos(x)=sin(x)*cos(x);
de: = 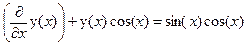
> dsolve(de,y(x));
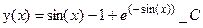 1
1
Задание 7. Найти общее решение дифференциального уравнения второго порядка y ''-2 y '+ y =sin x + e - x.
> restart;
> deq:=diff(y(x),x$2)-2*diff(y(x),x)+y(x)
=sin(x)+exp(-x);
deq:= 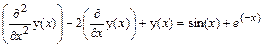
> dsolve(deq,y(x));
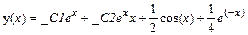
Задание 8. Найти решение задачи Коши:
y (4)+ y ''=2cos x, y (0)=-2, y '(0)=1, y ''(0)=0, y '''(0)=0.
> de:=diff(y(x),x$4)+diff(y(x),x$2)=2*cos(x);
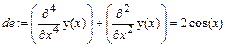
> cond:=y(0)=-2, D(y)(0)=1, (D@@2)(y)(0)=0,
(D@@3)(y)(0)=0;
cond:= y(0)=-2, D(y)(0)=1, (D(2))(y)(0)=0, (D(3))(y)(0)=0
> dsolve({de,cond},y(x));
y(x)=-2cos(x)- x sin(x)+ х
Задание 9. Найти решение краевой задачи:
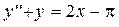 ,
, 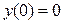 ,
, 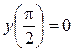 . Построить график решения.
. Построить график решения.
> restart; de:=diff(y(x),x$2)+y(x)=2*x-Pi;
de: = 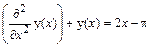
> cond:=y(0)=0,y(Pi/2)=0;
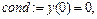
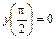
> dsolve({de,cond},y(x));
y(x)=2 x -p+pcos(x)
Замечание: для построения графика решения предварительно следует отделить правую часть полученного выражения.
> y1:=rhs(%):plot(y1,x=-10..20,thickness=2);

Задание 10. Найти решение системы дифференциальных уравнений:
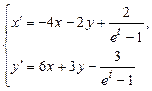
> sys:=diff(x(t),t)=-4*x(t)-2*y(t)+2/(exp(t)-1),
diff(y(t),t)=6*x(t)+3*y(t)-3/(exp(t)-1):
> dsolve({sys},{x(t),y(t)});
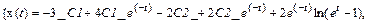
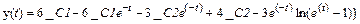
Найдены две функции x (t) и y (t), которые зависят от двух произвольных постоянных _ С1 и _ С2.
Задание 11. Нарисовать график решения дифференциального уравнения:
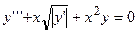 ,
, 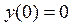 ,
, 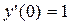 ,
, 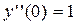
в интервале 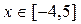 .
.
> restart; with(DЕtools):
> DEplot(diff(y(x),x$3)+x*sqrt(abs(diff(y(x),x)))
+x^2*y(x)=0, {y(x)}, =-4..5, [[y(0)=0,D(y)(0)=1,
(D@@2)(y)(0)=1]], stepsize=.1, linecolor=black,
thickness=2);

Задания для самостоятельной работы 
Задание 1. Найти значение первой и второй производных функции f(x).
| Вари-ант | Условие | Вари-ант | Условие |
а) 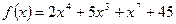 ;
б) ;
б) 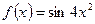 . .
| а) 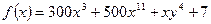 ;
б) ;
б) 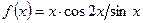 . .
| ||
а) 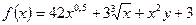 ;
б) ;
б) 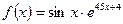 . .
| а) 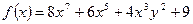 ;
б) ;
б) 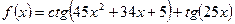 . .
| ||
а) 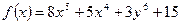 ;
б) ;
б) 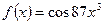 . .
| а) 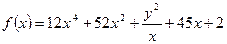 ;
б) ;
б) 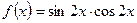 . .
| ||
а) 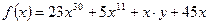 ;
б) ;
б) 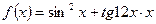 . .
| а) 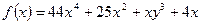 ;
б) ;
б) 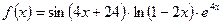 . .
| ||
а) 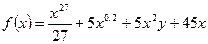 ;
б) ;
б) 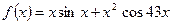 . .
| а) 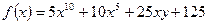 ;
б) ;
б) 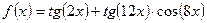 . .
|
Задание 2. Найти значение определенного интеграла, дать графическую интерпретацию решения.
| Вариант | Условие | Вариант | Условие |
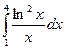
| 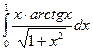
| ||
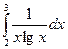
| 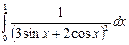
| ||
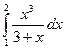
| 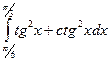
| ||
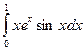
| 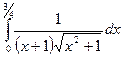
| ||
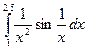
| 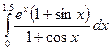
| ||
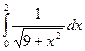
| 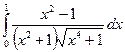
| ||
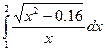
| 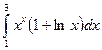
| ||
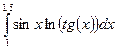
| 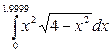
| ||
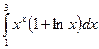
| 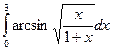
| ||
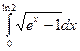
| 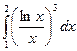
|
Задание 3. Решить дифференциальное уравнение и систему дифференциальных уравнений. Проиллюстрировать решение графически.
| Вариант | Условие | Условие |
| y''(x)=x∙sin(x) y(0)=1, y′(0)=2, y′′(0)=1 | 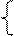 y′ = y∙z + x;
z′= x2 - y2.
y(0)=1, z(0)=2; y′ = y∙z + x;
z′= x2 - y2.
y(0)=1, z(0)=2;
| |
| y′′′(x)+2y′(x)=x2; y(0)=1, y′(0)=2, y′′(0)=1 |  y′= y∙x + 2∙z;
z′ = y - 4∙z.
y(1)=1, z(1)=0. y′= y∙x + 2∙z;
z′ = y - 4∙z.
y(1)=1, z(1)=0.
| |
| y′′′(x)+2y′(x)=e2x; y(0)=1 y′(0)=2, y′′(0)=1 | 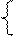 y′ = 4x2 + y/(x+1); z′ = e-(x2+y2) + z.
y(0)=1, z(0)=0.5, a=0, b=1 y′ = 4x2 + y/(x+1); z′ = e-(x2+y2) + z.
y(0)=1, z(0)=0.5, a=0, b=1
| |
| y′′′(x)+5y′(x)=e2x + sin(4x); y(0)=1, y′(0)=2, y′′(0)=1 | y′ = y∙z/x;
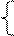 z′ = x/z;
y(1)=0, z(1)=0.5. z′ = x/z;
y(1)=0, z(1)=0.5.
| |
| 10y′′(x)+7y′(x)=e7x y(0)=1, y′(0)=2 | y′ = ln(2∙x + (9x2 +z2)1/2);
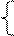 z′ = (9x2 +y2)1/2)+x∙sin(2∙x);
y(0)=0, z(0)=0.5. z′ = (9x2 +y2)1/2)+x∙sin(2∙x);
y(0)=0, z(0)=0.5.
| |
| 10y′′+2y′=x∙sin(4x) y(0)=1, y′(0)=2 | y′ = z2 + x;
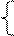 z′ = y∙x;
y(1)=0, z(1)=10. z′ = y∙x;
y(1)=0, z(1)=10.
| |
| 5y′′(x)+y′(x)=x∙e-x y(0)=1, y′(0)=2 | y′ = y∙cos(x) – z∙sin(x);
 z′ = y∙sin(x)+ z∙cos(x);
y(0)=0, z(0)=2. z′ = y∙sin(x)+ z∙cos(x);
y(0)=0, z(0)=2.
| |
| 3∙z′′(x)+z′(x)=x∙sin(x) z(0)=0, z′(0)=1 | y′ = 2∙cos(3∙y+z);
 z′ = x/(4∙y+x)+x+11;
y(0)=3, z(0)=3. z′ = x/(4∙y+x)+x+11;
y(0)=3, z(0)=3.
| |
| y′′′(x)+3∙y′′(x)=x2 y(0)=1, y′(0)=0 | y′ = y + x∙(x+5);
 z′ = x - z3;
y(0)=1, z(0)=-0.1. z′ = x - z3;
y(0)=1, z(0)=-0.1.
| |
| 4∙y′′(x)+2∙y′(x)=x2 y(0)=1, y′′(0)=0 | y′ = y∙z + x∙cos(x);
 z′ = -z2 +10 ∙x;
y(0)=0, z(0)=0.2. z′ = -z2 +10 ∙x;
y(0)=0, z(0)=0.2.
|
 2015-05-10
2015-05-10 384
384







