Электрическое поле. Напряженность электрического поля

Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку заряд оказывается под действием силы. Следовательно, для обнаружения и исследования электрического поля нужно воспользоваться некоторым пробным зарядом q. Согласно закону Кулона на пробный заряд действует сила

.

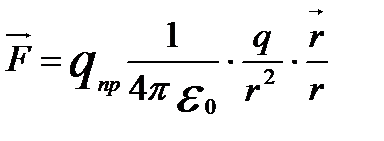Отношение 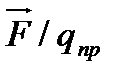для всех пробных зарядов будет одним и тем же и зависит лишь от величин q и r, определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле:

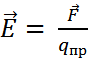(5)

Эту векторную величину называют напряженностью электрического поля в данной точке. Напряженность электрического поля численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Направление вектора 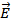совпадает с направление силы, действующей на положительный заряд.

Напряженность поля точечного заряда пропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля

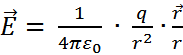(6)

Направлен вектор 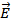вдоль прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен. За единицу напряженности электрического поля принимается напряженность в такой точке, в которой на заряд, равный единице (1 Кл в СИ), действует сила, равная единице (1 Н в СИ)

.

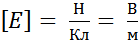Согласно приведенной формуле, сила, действующая на пробный заряд

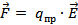
Очевидно, что на всякий точечный заряд q в точке поля с напряженностью 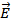будет действовать сила

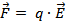(7)

Если заряд положителен, направление силы совпадает с направлением вектора 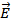. В случае отрицательного q направление векторов 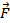и? 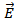противоположны.

Было указано ранее, что сила, с которой система зарядов действует на некоторый, не входящий в систему заряд равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности (4). Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:

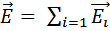(8)

Это принцип суперпозиции (наложения электрических полей). Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов.

Линии напряженности. Поток вектора напряженности. Электрическое поле можно описать определив для каждой точки величину и направление вектора 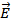. Совокупность этих векторов образует поле вектора напряженности электрического поля. Электрическое поле можно описать с помощью линий напряженности 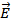, которые также будем называть силовыми линиями. Линии напряженности проводятся таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора 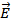(рис.1). Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению вектора 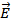. Тогда по картине линий напряженности можно судить о направлении и величине вектора 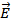в разных точках пространства.

Линии 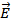точечного заряда представляют собой совокупность радиальных прямых, от заряда, если он положителен, и к заряду если он отрицателен (рис.2). Линии одним концом опираются на заряд, другим уходят в бесконечность. Полное число линий N, пересекающих сферическую поверхность произвольного радиуса r,будет равно произведению густоты линий на поверхность сферы 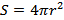. Густота линий по условию численно равна: .

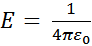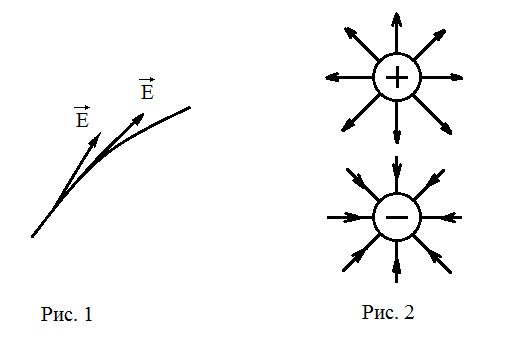
Следовательно, N равно

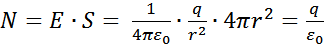
Число линий на любом расстоянии от заряда будет одно и то же. Отсюда вытекает, что силовые линии нигде, кроме заряда, не начинаются и не заканчиваются. Линии начавшись на положительном заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на отрицательном заряде. Это свойство линий 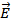является общим для всех электрических полей.

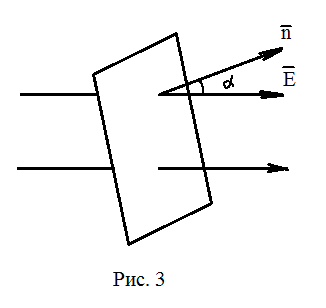
Поскольку густота линий 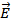выбирается равной численному значению E, количество линий, пронизывающих площадку 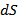, перпендикулярную вектору 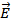, будет численно равно

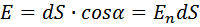
Где 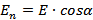– составляющая вектора 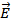по направлению нормали к площадке (рис.3). Отсюда для количества линий E, пронизывающих произвольную поверхность получется следующее выражение

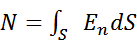, (10)

которое называется потоком вектора 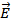через поверхность S. N численно равен количеству линий 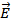, пронизывающих поверхность S. Поток есть алгебраическая величина, причем знак его зависит от выбора направления нормали к площадке dS. Изменение направления нормали на противоположно изменяет знак у 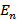и, следовательно, у N.