Теорема Гаусса и ее применение к вычислению напряженности полей

Ранее было показано, что окружающую точечный заряд q сферическую поверхность любого радиуса r пересекает 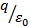линии E. Поток вектора 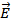через некоторую поверхность численно равен количеству линий, пересекающих эту поверхность, и также равен 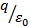. Это утверждение справедливо для замкнутой поверхности любой формы.

Пусть внутри некоторой замкнутой поверхности заключено насколько точечных зарядов произвольных знаков 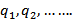. Поток вектора 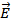по определению равен

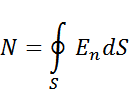
В силу принципа суперпозиции полей

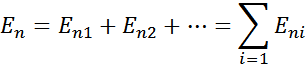
Подставив данное выражение в выражение для потока, получим

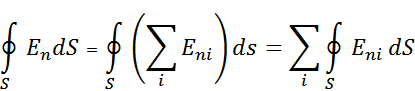
Где 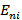– нормальная составляющая напряженности поля создаваемого i -м зарядом в отдельности. Но, как было показано выше,

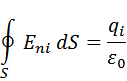
следовательно

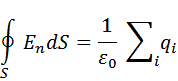
Это утверждение носит название теоремы Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .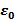

В частности, если внутри поверхности заряды отсутствуют, поток равен нулю.

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью 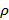, теорема Гаусса имеет следующий вид:

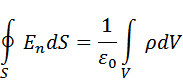
Где интеграл справа берется по объему V, охватываемому поверхностью S, а 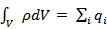. Теорема Гаусса позволяет в ряде случаев просто найти напряженность поля.