Математической моделью машины является следующее дифференциальное уравнение (см. лаб. раб №1)
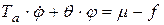 .
.
Математическую модель регулятора прямого действия в общем виде можно представить дифференциальным уравнением (см. лаб. раб №2 и №3)
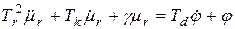 ,
,
где 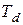 - характеризует свойство регулятора управлять по скорости (принцип Сименсов),
- характеризует свойство регулятора управлять по скорости (принцип Сименсов), 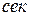 .
.
Математической моделью системы «машина-регулятор прямого действия» будет следующая система уравнений
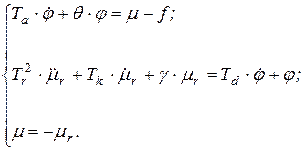
После преобразования по Лапласу систему можно представить в виде следующей структурной схемы
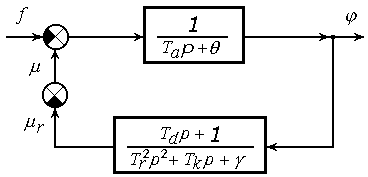
Характеристический полином системы
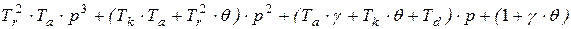 .
.
Приведенный характеристический полином системы
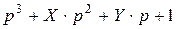 ,
,
где
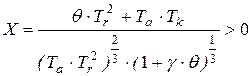 ,
, 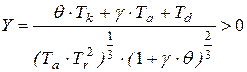 - безразмерные
- безразмерные
положительные параметры Вышнеградского.
Условие устойчивости (условие отрицательности всех трех корней в характеристическом уравнении) в параметрах Вышнеградского (см. лекцию №3)
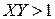 .
.
Условие монотонности (плавности) переходного процесса (отрицательность и вещественность всех трех корней - наилучшее качество регулирования).
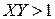 ,
, 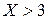 ,
, 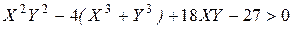 . (3.11)
. (3.11)
Условие слабой колебательности переходного процесса (вещественный корень по отношению к паре комплексно сопряженных корней находится ближе к оси мнимых значений корней)
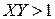 ,
, 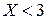 ,
, 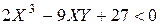 (3.11)
(3.11)
Условие сильной колебательности переходного процесса (пара комплексно сопряженных корней по отношению к вещественному корню находится ближе к оси мнимых значений корней)
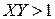 ,
, 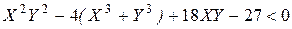 ,
, 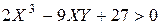 .
.
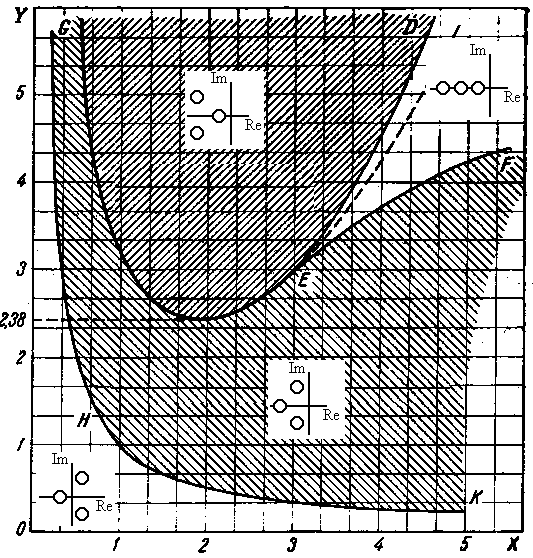
В соответствии с полученными условиями структура разбиения плоскости параметров 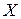 -
- 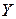 - диаграмма Вышнеградского, определяется следующими граничными линиями:
- диаграмма Вышнеградского, определяется следующими граничными линиями:
1) 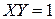 ;
;
2) 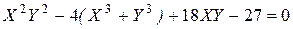 при
при 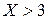 ;
;
3) 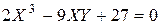 при
при 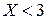 .
.
 2015-05-10
2015-05-10 184
184






