Ниже приведены формулы аналитической геометрии, используемые при вычислении размеров, оклонений формы и расположения поверхностей.
Уравнение прямой, проходящей через 2 точки 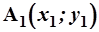 и
и 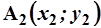 (см. рис.6), записывается как
(см. рис.6), записывается как
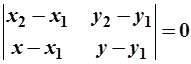 (1)
(1)
или
 |
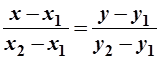 . (2)
. (2)
Рис.6
Расстояние от точки 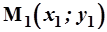 до прямой, заданной уравнением
до прямой, заданной уравнением 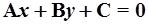 (см. рис.7), определяется как
(см. рис.7), определяется как
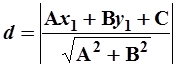 (3)
(3)
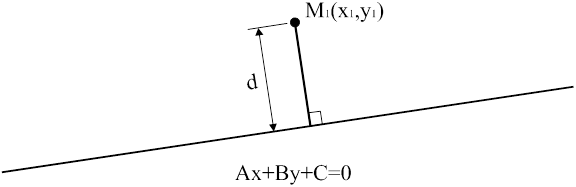 |
Рис.7
Расстояние между 2 точками 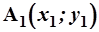 и
и 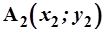 (см. рис.8) определяется как
(см. рис.8) определяется как
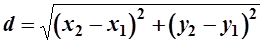 (4)
(4)
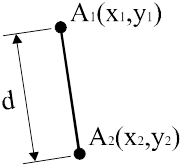 |
Рис.8
Расстояние между 2 параллельными прямыми, заданными уравнениями 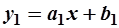 и
и 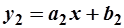 (см. рис.9), определяется следующим образом.
(см. рис.9), определяется следующим образом.
4.1. Задание " т. 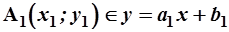
.2. Определение расстояния от т. 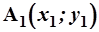 до прямой
до прямой 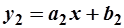 (см. п. 2).
(см. п. 2).
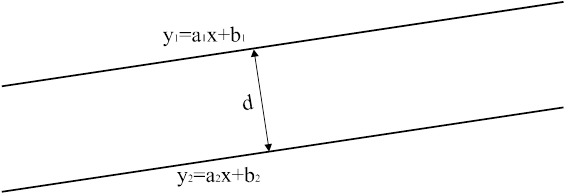 |
Рис.9
Уравнение прямой, проходящей через т. 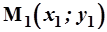 параллельно прямой, заданной уравнением
параллельно прямой, заданной уравнением 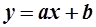 (см. рис.10), определяется как
(см. рис.10), определяется как
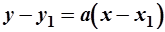 ; (5)
; (5)
а заданной уравнением 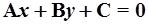 - как
- как
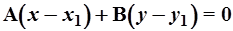 . (6)
. (6)
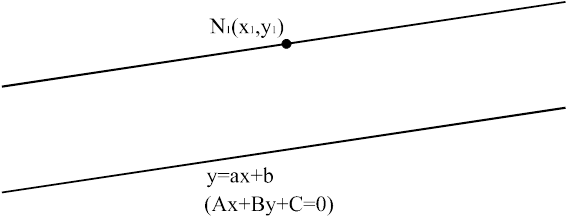 |
Рис.10
Уравнение прямой, проходящей через т. 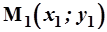 перпендикулярно прямой, заданной уравнением
перпендикулярно прямой, заданной уравнением 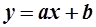 (см. рис.11), определяется как
(см. рис.11), определяется как
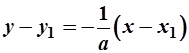 ; (7)
; (7)
а заданной уравнением 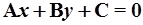 - как
- как
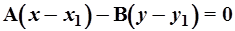 . (8)
. (8)
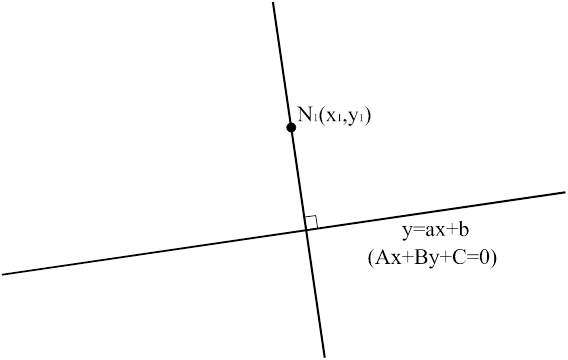 |
Рис.11
Угол между 2 прямыми, заданными уравнениями 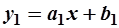 и
и 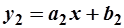 (рис.12), определяется как
(рис.12), определяется как
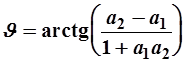 ; (9)
; (9)
а заданных уравнениями 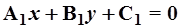 и
и 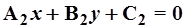 - как
- как
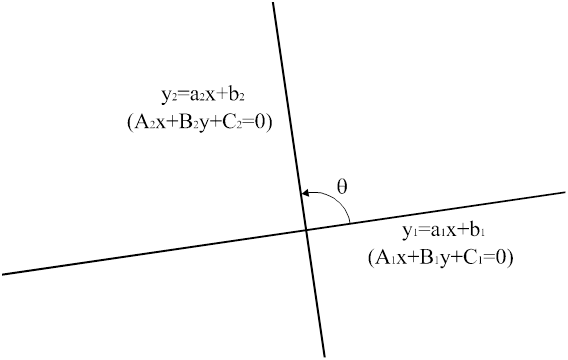 |
Рис.12
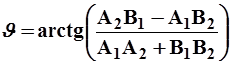 . (10)
. (10)
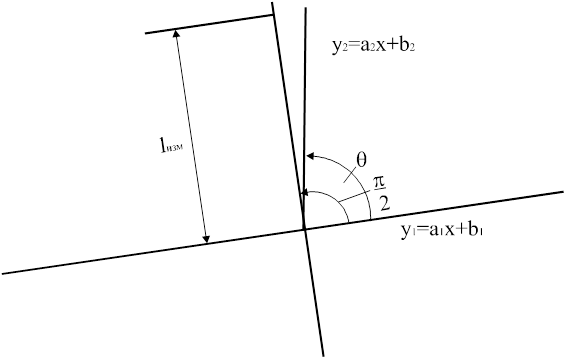
Отклонение от перпендикулярности 2 прямых (см. рис. 13) определяется следующим образом.
8.1. Определение угла между 2 прямыми.
8.2. Максимальное отклонение от перпендикулярности на базовой длине определяется по формулам 11 или 11а (Можно использовать, если отклонение от перпендикулярности очень мало. Углы задаются в радианах!):
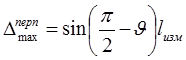 . (11)
. (11)
 |
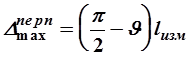 . (11а)
. (11а)
Рис.13
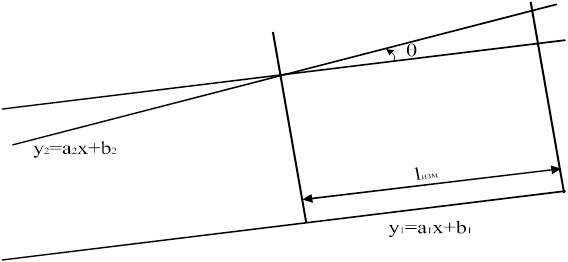
Отклонение от параллельности 2 прямых (см. рис. 14) определяется следующим образом.
9.1. Определение угла между 2 прямыми.
9.2. Максимальное отклонение от параллельности на базовой длине определяется по формулам 12 или 12а
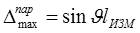 . (12)
. (12)
 |
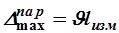 . (12а)
. (12а)
Рис.14
Задание уравнения окружности по 3 точкам (см. рис. 15).
10.1. Общее уравнение окружности:
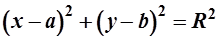 ; (13)
; (13)
10.2. Условие существования окружности:
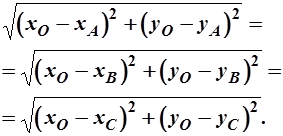 (14)
(14)
10.3. Определение центра окружности:
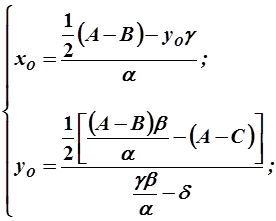 (15)
(15)
где
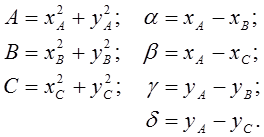 (16)
(16)
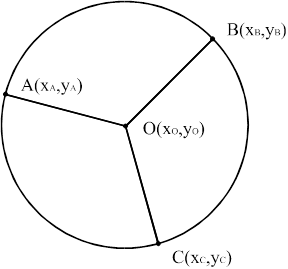 |
Рис.15
 2015-05-10
2015-05-10 548
548








