Ход работы
1. 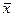 =37,67,
=37,67, 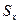 =10,81,
=10,81, 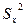 =116,958;
=116,958; 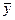 = 19,61,
= 19,61, 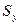 = 6,26,
= 6,26, 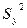 = 39,174.
= 39,174.
2. Найдем условные средние 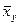 и
и 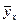 , запишем их в таблицу
, запишем их в таблицу
Таблица 10'
Корреляционная таблица с условными средними 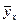 и
и 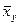
| Y/X | X1 16.2 | X2 22.57 | X3 28.94 | X4 35.31 | X5 41.68 | X6 48.05 | X7 54.42 | X8 60.8 | ny | 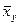
|
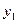 =
2.9 =
2.9
| - | - | - | - | - | - | - | 54,42 | ||
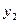 =
7.14 =
7.14
| - | - | - | - | 49,65 | |||||
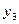 =
11.38 =
11.38
| - | - | - | 46,99 | ||||||
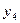 =
15.62 =
15.62
| - | 41,68 | ||||||||
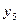 =
19.86 =
19.86
| - | 33,19 | ||||||||
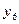 =
24.1 =
24.1
| - | - | - | 35,01 | ||||||
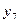 =
28.34 =
28.34
| - | - | - | 33,19 | ||||||
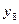 =
32.6 =
32.6
| - | - | - | - | - | - | 28,94 | |||
| nx | ||||||||||
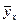
| 23,05 | 20,39 | 23,46 | 21,66 | 17,88 | 16,47 | 12,44 | 14,56 |
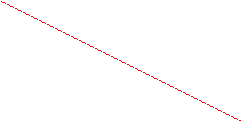 3. На корреляционном поле (таблица 2, лабораторная работа № 1) строим эмпирическую линию регрессии
3. На корреляционном поле (таблица 2, лабораторная работа № 1) строим эмпирическую линию регрессии 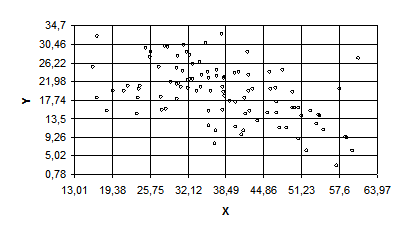
4. Найдем эмпирический исправленный корреляционный момент по формуле
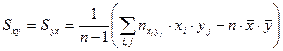 , заполнив таблицу для подсчета
, заполнив таблицу для подсчета 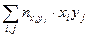 :
:
Таблица 11
| хi | yj | 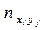
| хi yj 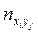
| хi | yj | 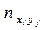
| хi yj 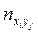
|
| 16,2 | 15,62 | 253,044 | 41.68 | 11.38 | 1897,274 | ||
| 16,2 | 19,86 | 321,732 | 41.68 | 15.62 | 2604,166 | ||
| 16,2 | 24,1 | 390,42 | 41.68 | 19.86 | 2483,294 | ||
| 16,2 | 32,6 | 528,12 | 41.68 | 24.1 | 3013,464 | ||
| 22,57 | 15,62 | 352,5434 | 41.68 | 28.34 | 1181,211 | ||
| 22,57 | 19,86 | 2689,441 | 48.05 | 7.14 | 343,077 | ||
| 22,57 | 28,34 | 639,6338 | 48.05 | 11.38 | 1093,618 | ||
| 28,94 | 15,62 | 904,0856 | 48.05 | 15.62 | 5253,787 | ||
| 28,94 | 19,86 | 3448,49 | 48.05 | 19.86 | 2862,819 | ||
| 28,94 | 24,1 | 3487,27 | 48.05 | 24.1 | 2316,01 | ||
| 28,94 | 28,34 | 5741,117 | 54.42 | 2,9 | 157,818 | ||
| 35.31 | 7.14 | 252,1134 | 54.42 | 7.14 | 388,5588 | ||
| 35.31 | 11.38 | 803,6556 | 54.42 | 11.38 | 1238,599 | ||
| 35.31 | 15.62 | 1103,084 | 54.42 | 15.62 | 2550,121 | ||
| 35.31 | 19.86 | 4908,796 | 54.42 | 19.86 | 1080,781 | ||
| 35.31 | 24.1 | 8509,71 | 60.8 | 7.14 | 434,112 | ||
| 35.31 | 28.34 | 2001,371 | 60.8 | 11.38 | 1383,808 | ||
| 35.31 | 32.6 | 2302,212 |
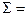 68919,36 68919,36
|
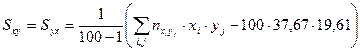 =
= 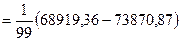 = -50,02.
= -50,02.
5. Находим теперь эмпирический коэффициент корреляции:
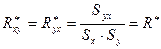
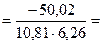 - 0,74.
- 0,74.
6. Проверим гипотезу Но: признаки Х и У - независимы друг от друга и коэффициент корреляции R = 0. Выясним, существенно ли отличается от нуля рассчитанный эмпирический коэффициент корреляции 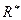 .
.
6.1. значение статистики 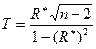
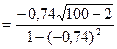 =-16,28;
=-16,28;
6.2. находим 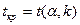 =1,99 (k=n- 2) [2, приложение 6, с.466];
=1,99 (k=n- 2) [2, приложение 6, с.466];
6.3. получили, что 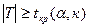 , а значит гипотеза Но - неверна, эмпирический коэффициент корреляции существенно отличен от нуля. Принимаем альтернативную гипотезу Н1: в генеральной совокупности коэффициент корреляции не равен нулю и Х и У – линейно зависимы.
, а значит гипотеза Но - неверна, эмпирический коэффициент корреляции существенно отличен от нуля. Принимаем альтернативную гипотезу Н1: в генеральной совокупности коэффициент корреляции не равен нулю и Х и У – линейно зависимы.
7. Найдем тогда уравнение линейной зависимости признаков: рассчитаем эмпирические коэффициенты линейной регрессии У на Х (или Х на У) 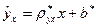 :
:
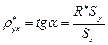
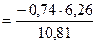 =-0,43;
=-0,43;
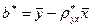
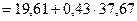 =35,75;
=35,75;
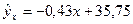 ,
,
аналогично 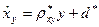 , где
, где
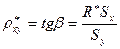
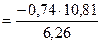 =1,28;
=1,28;
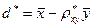
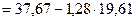 =12,61;
=12,61;
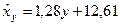 .
.
8. Проверим теперь значимость уравнения регрессии У на Х:
8.1. 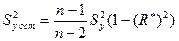
 =17,9,
=17,9,
8.2. статистика 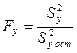
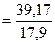 =2,19.
=2,19.
Аналогично для проверки гипотезы значимости уравнения регрессии Х на У:
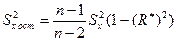
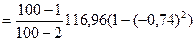 =53,17;
=53,17;
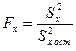
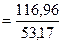 =2,20.
=2,20.
8.3. Значение 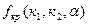 = 1,3 (
= 1,3 (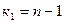 =99,
=99, 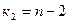 =98).
=98).
8.4. 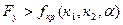 и
и 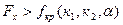 , значит, гипотеза принимается, т.е. уравнение
, значит, гипотеза принимается, т.е. уравнение 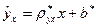 и уравнение
и уравнение 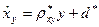 статистически значимо описывает результаты эксперимента.
статистически значимо описывает результаты эксперимента.
9. Найдем интервальные оценки коэффициента корреляции R и коэффициента линейной регрессии 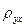 по формулам (
по формулам (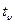 =1,98):
=1,98):
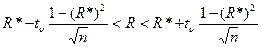 , -0,83 < R < -0,65;
, -0,83 < R < -0,65;
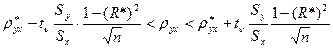 , -0,48
, -0,48 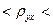 -0,38.
-0,38.
10.Найдем значения 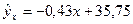 и
и 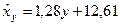 для середин интервалов Х i и У j и внесем их в корреляционную таблицу (дописав еще одну строку и один столбец к таблице 10):
для середин интервалов Х i и У j и внесем их в корреляционную таблицу (дописав еще одну строку и один столбец к таблице 10):
Таблица 12
| Y/X | X1 16.2 | X2 22.57 | X3 28.94 | X4 35.31 | X5 41.68 | X6 48.05 | X7 54.42 | X8 60.8 | ny | 
| 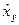
|
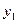 =
2.9 =
2.9
| - | - | - | - | - | - | - | 54,42 | 16,32 | ||
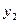 =
7.14 =
7.14
| - | - | - | - | 49,65 | 21,75 | |||||
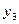 =
11.38 =
11.38
| - | - | - | 46,99 | 27,18 | ||||||
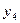 =
15.62 =
15.62
| - | 41,68 | 32,60 | ||||||||
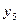 =
19.86 =
19.86
| - | 33,19 | 38,03 | ||||||||
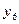 =
24.1 =
24.1
| - | - | - | 35,01 | 43,46 | ||||||
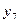 =
28.34 =
28.34
| - | - | - | 33,19 | 48,89 | ||||||
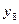 =
32.6 =
32.6
| - | - | - | - | - | - | 28,94 | 54,34 | |||
| nx | |||||||||||
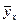
| 23,05 | 20,39 | 23,46 | 21,66 | 17,88 | 16,47 | 12,44 | 14,56 | |||
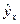
| 28,78 | 26,04 | 23,31 | 20,57 | 17,83 | 15,09 | 12,35 | 9,61 |
11.Построим на корреляционном поле, например, эмпирическую линию регрессии У на Х:
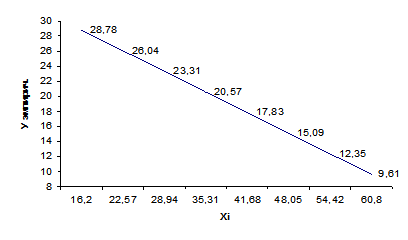
Вывод: Сравнивая 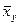 и
и 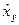 ,
, 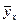 и
и 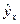 (таблица 12), видим, что уравнения регрессии хорошо согласуются с данными выборки (обратите внимание – особенно У). В силу того, что значение
(таблица 12), видим, что уравнения регрессии хорошо согласуются с данными выборки (обратите внимание – особенно У). В силу того, что значение 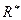 отрицательно и довольно близко к единице, мы подтверждаем уже замеченную из графика эмпирической линии регрессии, что зависимость между наблюдаемыми признаками – обратная: чем больше процент прочности бетона на сжатие, тем меньше процент сопротивления бетона на разрыв.
отрицательно и довольно близко к единице, мы подтверждаем уже замеченную из графика эмпирической линии регрессии, что зависимость между наблюдаемыми признаками – обратная: чем больше процент прочности бетона на сжатие, тем меньше процент сопротивления бетона на разрыв.
 2015-05-10
2015-05-10 288
288







