2015-05-10
2350
Если разность |p-q| мала, то произведение n = pq легко разлагается на множители с помощью алгоритма Ферма.
Ввод: нечетное натуральное число n.
Вывод: множитель числа n или сообщение о том, что n простое.
Шаг 1. Положить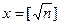 
. Если n = х2, то х является делителем числа n, и работа алгоритма останавливается; в противном случае увеличить х на 1 и перейти к шагу 2.
Шаг 2. Если х = (n + 1) / 2, то число n простое, и работа алгоритма останавливается; в противном случае вычислить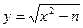 
.
Шаг 3. Если число у целое (т.е., если [у]2 = х2 - n), то n раскладывается в произведение (х + у)(х - у), и работа алгоритма останавливается; в противном случае увеличить х на 1 и перейти к шагу 2.
Как показывает следующий пример, этот алгоритм очень прост в применении. Допустим, мы хотим разложить на множители число n = 1 342 127. Сначала переменной х присваивается целая часть числа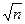 
. В примере она равна х = 1158. Однако
х 2 = 11582 = 1 340 964 < 1 342 127.
Поэтому мы должны увеличить х на 1. Мы продолжим этот процесс до тех пор, пока число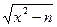 
не станет целым или не будет выполняться равенство х = (n+1) / 2. Заметим, что в нашем примере (n + 1) / 2 = 671064. Значения переменных х и у после завершения каждого цикла приведены в таблице.
|
|
|
| x |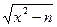
|
| 33,97… | |
| 58,93… | |
| 76,11… | |
| 90,09… | |
| 102,18… | |
Таким образом, на шестом цикле мы получили целое число. Значит, искомые числа х = 1164 и у = 113. Соответствующие множители равны
х + у = 1277 и x - у = 1051.
Разложение n на p и q по φ(n)
Если n = pq и φ(n) = (p-1)(q-1) известны, то
φ(n) = (p-1)(q-1) = pq – (p+q) + 1 = n – (p + q) + 1,
так что сумма искомых простых делителей p + q = n - φ(n) + 1 известна. Далее,
(p+q)2 – 4n = (p2 + q2 + 2pq) – 4pq = (p - q)2,
поэтому разность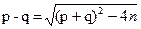 
тоже известна. Теперь, решая простую систему линейных уравнений, находим p и q.
Приложение 3. Алгоритмы арифметических вычислений
Модульное умножение A × B mod n
Для более эффективной работы алгоритма полезно представить множитель B в двоичной системе счисления:
B = bk2k + bk-12k-1 + … + b12 + b0,
где коэффициенты b0,…,bk могут принимать значения 0 или 1.
А умножение B на А производить поразрядно в цикле сразу же при этом вычисляя остаток от деления на n:
R = 0
for i from k to 0 do R = (2*R + A*bi ) mod n
return (R)
Модульная редукция B mod n
Суть метода Барета заключается в вычислении значения R = B mod n, для чего предварительно вычисляется m = [22k / n]. Эти числа можно запомнить, если выполняются многократные вычисления с использованием данного модуля:
Входные данные:
B = b2k-122k-1 + … + b12 + b0;
n = nk-12k-1 + … + n12 + n0 (mk-1 = 0);
m = 22k div n.
q1 = b div 2k-1
q2 = q1 m
q3 = q2 div 2k+1
r1 = b mod 2 k+1
r2 = (q3 n) mod 2 k+1
r = r1 – r2
if r < 0 then r = r + 2k+1
while r >= n do r = r – n
return (r)
Несмотря на то, что в данном алгоритме производится большое количество операций деления, все они легко реализуются с помощью правого сдвига. При этом следует учитывать, что q2 используется для вычисления q3. В связи с этим в q2 используется только k+1 младших разрядов.
|
|
|
