2015-05-13
411
Задание
В пределах некоторого экономического района имеются четыре карьера, производящих нерудное сырье, и четыре пункта потребления (заводы железобетонных изделий, строительные и дорожные организации и т.п.). Требуется определить объем перевозок готовой продукции от j -го карьера i-му потребителю.
При этом известны нужды каждого потребителя в нерудном сырье, объемы производства на каждом карьере и стоимость перевозки 1м3 продукции с j - го карьера i - му потребителю.
Условия транспортной задачи заданы матрицей (таблица 4.2).
Таблица 4.2
| Поставщик j | Потребитель i | Запасы груза А | |||
| 5[4] | |||||
| Потребность в грузе А |
Решение транспортной задачи включает два основных этапа: построение опорного решения (начального плана перевозок) и построение оптимального решения.
Перед построением опорного решения проверяется баланс запасов и потребления, т.е. является ли модель закрытой. Суммарные запасы составляют 120+140+230+200=690 единиц груза, а суммарная потребность - 160+190+210+240=800 единиц груза. Так как суммарная потребность превышает объём запасов, вводим пятого фиктивного поставщика с запасами 800-690=110 единиц. Стоимости перевозок от фиктивного поставщика равны 0. Получена новая матрица для закрытой модели с пятью поставщиками (таблица 4.3).
|
|
|
Таблица 4.3
| Поставщик j | Потребитель i | Запасы груза А | |||
| Потребность в грузе А |
Построение опорного решения может осуществляться методами северо-западного угла, наименьших стоимостей и двойного предпочтения.
При применении метода северо-западного угла данные о стоимостях не нужны. Рассматривается клетка 11 (северо-западный угол) и в нее на основании сравнения величин потребности первого потребителя (160) и запаса первого поставщика (120) проставляется минимальная из сравниваемых величин (120<160, значит 120). Так как запасы первого поставщика удовлетворены (х11 =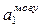 
), то первая строка «вычёркивается» из рассмотрения, и определяется разность по столбцу - оставшаяся неудовлетворённой потребность первого покупателя: (
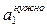- x11) или (160-120=40). Далее рассматривается клетка 21 (новый северо-западный угол) и сравниваются величины оставшейся потребности первого покупателя (40) и возможности второго поставщика (140). B клетку 21 проставляется минимальная из этих величин. Подобная процедура повторяется вплоть до заполнения всей матрицы. Построение опорного решения транспортной задачи методом северо-западного угла представлено в таблице 4.4.
|
|
|
Таблица 4.4
| Поставщик j | Потребитель i | Запасы груза А | |||
| Потребность в грузе А |
Совокупные затраты при этом составят 2550.
При использовании метода наименьших стоимостей последовательно заполняются клетки, содержащие наименьшие стоимостные показатели. При этом в эти клетки проставляется допустимый объем перевозок, для чего сопоставляются объемы запасов и потребности (аналогично методу северо-западного угла). Так в нашем случае, первой в рассмотрении участвует ячейка 32 или 44 с наименьшей ненулевой стоимостью перевозки (2). Процедура повторяется до получения допустимого решения.
Построение опорного решения транспортной задачи методом наименьших стоимостей представлено в таблице 4.5.
Таблица 4.5
| Поставщик j | Потребитель i | Запасы груза А | |||
| Потребность в грузе А |
Совокупные затраты при этом составят 2300.
При использовании метода двойного предпочтения последовательно заполняются клетки, содержащие наименьшие стоимостные показатели и по столбцу и по строке. Просматриваем строки и отмечаем клетки, имеющие минимальные стоимости: 11, 12, 22, 32 и 44. Затем просматриваем столбцы и также отмечаем клетки с минимальными стоимостями: 31, 32, 43 и 44. Клетки 32 и 44 отмечены дважды - проставляем в них возможные объемы перевозок (соответственно 190 и 200). Далее повторяем процедуру определения ячеек с двойным предпочтением. По строкам лучшие – 11, 21, 24, 31, по столбцам – 31, 33, 24. Клетки 31 и 24 отмечены дважды - проставляем в них возможные объемы перевозок (соответственно 40 и 40). Повторяем указанную последовательность действий до полного заполнения матрицы.
Построение опорного решения транспортной задачи методом двойного предпочтения представлено в таблице 4.6. Данный план перевозок аналогичен плану перевозок, полученному ранее методом наименьших стоимостей. Совокупные затраты при этом составят 2300.
Таблица 4.6
| Поставщик j | Потребитель i | Запасы груза А | |||
| Потребность в грузе А |
После построения опорного решения транспортной задачи, необходима его проверка на оптимальность и, при выяснении его неоптимальности, собственно оптимизация.
Один из наиболее простых и распространенных методов оптимизации транспортной задачи - метод потенциалов. Оптимизируем для примера полученный методом северо-западного угла план перевозок (таблица 4.4). Предположительно, он должен быть неоптимальным, так как существует план перевозок, полученный методом двойного предпочтения и методом наименьших стоимостей, с меньшими совокупными затратами на перевозку грузов. На первом этапе оптимизации методом потенциалов происходит присвоение и расчет системы потенциалов. Обычно полагают Uj=0, присваивая нулевой потенциал строке j, имеющей занятую перевозкой клетку с наибольшей стоимостью. В нашем случае это любая из строк 1, 2 или 3, имеющая перевозку и наибольшую стоимость перевозок (5) из всех ячеек, имеющих перевозки. Выберем строку 1 в качестве начальной для расчёта системы потенциалов. Далее потенциалы всех остальных столбцов и строк вычисляют через занятые клетки (xji>0), используя следующее условие оптимальности:
|
|
|
сji=Vi-Uj (4.5)
Так, например, V1=c11+U1 или V3=5+0=5 и т.д.
В таблице 4.7 представлена построенная таким образом система потенциалов.
На втором этапе оптимизации происходит собственно проверка первоначального плана на оптимальность, а именно проверка выполнения для всех клеток, не занятых перевозками (xji=0), следующего условия:
сji³Vi-Uj (4.6).
Если условие выполняется для всех клеток, не занятых перевозками (xji=0), то план является оптимальным, иначе план может быть улучшен.
Таблица 4.7
| Потенциал Uj | Потенциал Vi | Запасы груза А | |||
| V1=5 | V2=4 | V3=7 | V4=6 | ||
| U1=0 | |||||
| U2=0 | |||||
| U3=2 | |||||
| U4=4 | |||||
| U5=6 | |||||
| Потребность в грузе А |
После вычисления проверочных условий, выяснилось, что для ячеек 23, 24 и 53 условие оптимальности не выполняется:
23) 7 – 0=7 > 6
24) 6 – 0=6 > 5 (4.7)
53) 7 – 6=1 > 0.
Таким образом, необходима оптимизация плана перевозок. В связи с этим выполняется третий этап оптимизации - выбор клетки с максимальным превышением разности потенциалов над стоимостью перевозки (это превышение характеризует экономию на перевозке единицы груза при изменении плана перевозок) и составление замкнутого контура, вершинами которого являются выбранная клетка с нарушением и клетки с перевозками.
Для нашего случая нет разницы, какую клетку с нарушением выбрать в качестве вершины оптимизационного контура, так как величина экономии при всех вариантах изменения плана одинакова и равна 1:
23) 7 – 6 =1
24) 6 – 5 =1 (4.8)
53) 1 – 0 =1.
Оптимизационные контуры каждого из вариантов улучшения плана представлены в таблицах 4.8 - 4.10. Контур может иметь различную конфигурацию, но в нём всегда чётное количество вершин.
Таблица 4.8
Таблица 4.9
Таблица 4.10
Начиная с клетки, имеющей нарушение, вершины контура нумеруются (по часовой стрелке или против). Нечетные вершины составляют положительную полуцепь, а четные - отрицательную. При улучшении плана в вершинах положительной полуцепи (нечетных) объемы перевозок увеличиваются, а в вершинах отрицательной полуцепи (четных) уменьшаются на величину минимального объёма перевозок в чётных клетках.
|
|
|
Выберем для оптимизации ячейку 23, тогда оптимизационный контур будет соответствовать таблице 4.8. Пронумеруем его и определим минимальный объём перевозок в чётных вершинах – min(100,140)=100. После этого перераспределяем объемы перевозок внутри контура, для чего к объемам перевозок в нечетных вершинах прибавляем объем 100, а из объемов перевозок в четных вершинах вычитаем эту величину (таблица 4.11).
Таблица 4.11
 4
= 100 -100
| =+100 | ||
| =90+100 | =140-100 | ||
В результате процедуры оптимизации получают улучшенный план, в котором общие затраты на перевозку меньше, чем в предыдущем плане, на величину = 1(предполагаемая экономия от улучшения плана на единицу объёма перевозок) * 100 (непосредственно изменения в плане по объёму). Затраты после первой итерации оптимизации составят 2550-100=2450. Новый план является допустимым, так как в каждой строке и столбце замкнутого контура в одной клетке объем увеличился, а в другой уменьшился на одну и ту же величину. Однако, этот результат хуже полученного другими методами планирования перевозок (2450>2300), следовательно, предположительно, он требует дополнительной оптимизации.
Строим по вышеизложенным правилам новую систему потенциалов (таблица 4.12). После вычисления проверочных условий, выяснилось, что для ячеек 31 и 53 условие оптимальности не выполняется:
31) 5 – 1=4 > 3, 53) 6 – 5=1 > 0 (4.9)
Таким образом, подтвердилась необходимость дальнейшей оптимизации плана перевозок. В связи с этим повторяем все шаги оптимизации, выполняя вторую итерацию улучшения плана.
Выберем для оптимизации ячейку 31 и построим оптимизируемый контур. Пронумеруем его и определим минимальный объём перевозок в чётных вершинах – min(40,40)=40. После этого перераспределяем объемы перевозок внутри контура, для чего к объемам перевозок в нечетных вершинах прибавляем объем 40, а из объемов перевозок в четных вершинах вычитаем эту величину. В результате второй итерации процедуры оптимизации затраты составят 2450-40=2410. Однако, этот результат вновь хуже полученного другими методами планирования перевозок (2410>2300), следовательно, предположительно, он ещё требует оптимизации. Строим новую систему потенциалов (таблица 4.13).
Таблица 4.12
| Потенциал Uj | Потенциал Vi | Запасы груза А | |||
| V1=5 | V2=3 | V3=6 | V4=5 | ||
| U1=0 | |||||
| U2=0 | |||||
| U3=1 | |||||
| U4=3 | |||||
| U5=5 | |||||
| Потребность в грузе А |
Следует отметить, что полученный на второй итерации оптимизации план является вырожденным и правила построения системы потенциалов требуют уточнения для данного случая. При построении опорного решения или при его улучшении количество клеток, занятых перевозками, может оказаться меньше, чем (m+n-1). Это как раз наш случай: количество клеток с перевозками – 7 < 4+5-1 или 7 < 8. Для решения задачи в данном случае в клетку (или клетки) без перевозок проставляют фиктивную перевозку малого объема Q. При этом объемы перевозок добавляют в такое количество клеток, чтобы план стал невырожденным, т.е. количество заполненных клеток равнялось бы (m+n-1). После этого решают задачу как невырожденную, а в оптимальном плане Q заменяют нулями. Если клетка, в которой имеется перевозка Q, будет чётной вершиной контура, то объем перевозок, на который улучшается план, равен Q. Вставим фиктивную перевозку, равную 1 в ячейку 33.
Таблица 4.13
| Потенциал Uj | Потенциал Vi | Запасы груза А | |||
| V1=4 | V2=3 | V3=6 | V4=5 | ||
| U1=-1 | |||||
| U2=0 | |||||
| U3=1 | 1[5] | ||||
| U4=3 | |||||
| U5=5 | |||||
| Потребность в грузе А |
После вычисления проверочных условий, выяснилось, что для ячейки 53 условие оптимальности не выполняется:
53) 6 – 5=1 > 0 (4.10).
Таким образом, подтвердилась необходимость дальнейшей оптимизации плана перевозок. В связи с этим повторяем все шаги оптимизации, выполняя третью итерацию улучшения плана.
В результате третьей итерации процедуры оптимизации затраты составят 2410-70=2340. Однако, этот результат вновь хуже полученного другими методами планирования перевозок (2340>2300), следовательно, предположительно, он ещё требует оптимизации. Строим новую систему потенциалов (таблица 4.14).
Таблица 4.14
| Потенциал Uj | Потенциал Vi | Запасы груза А | |||
| V1=4 | V2=3 | V3=6 | V4=6 | ||
| U1=-1 | |||||
| U2=0 | |||||
| U3=1 | |||||
| U4=4 | |||||
| U5=6 | |||||
| Потребность в грузе А |
После вычисления проверочных условий, выяснилось, что для ячеек 14 и 24 условие оптимальности не выполняется:
14) 6 – (-1)=7 > 6, 24) 6 – 0=6 > 5 (4.11)
Таким образом, подтвердилась необходимость дальнейшей оптимизации плана перевозок. В связи с этим повторяем все шаги оптимизации, выполняя четвёртую итерацию улучшения плана.
Выберем для оптимизации ячейку 24. Оптимизационный контур будет соответствовать таблице 4.15. Пронумеруем его и определим минимальный объём перевозок в чётных вершинах – min(40,140)=40. После этого перераспределяем объемы перевозок внутри контура, для чего к объемам перевозок в нечетных вершинах прибавляем объем 40, а из объемов перевозок в четных вершинах вычитаем эту величину (таблица 4.15).
В результате четвёртой итерации процедуры оптимизации затраты составят 2340-40=2300. Этот результат в точности совпадает с полученными результатами при использовании метода наименьших стоимостей или двойного предпочтения (см. таблицы 4.5 или 4.6 с 4.16). Проверим этот план на оптимальность, построив систему потенциалов (таблица 4.16).
Таблица 4.15
| =140-40 | =+40 | ||
 40
|  6
| ||
 0
=70+40
| =40 - 40 |
После вычисления проверочных условий, выяснилось, что все ячейки удовлетворяют требуемым неравенствам, следовательно, план перевозок оптимален.
Таблица 4.16
| Потенциал Uj | Потенциал Vi | Запасы груза А | |||
| V1=4 | V2=3 | V3=6 | V4=5 | ||
| U1=-1 | |||||
| U2=0 | |||||
| U3=1 | |||||
| U4=3 | |||||
| U5=6 | |||||
| Потребность в грузе А |
Решим эту транспортную задачу симплекс-методом, используя средство «Поиск решений» Excel.
Напомним, что модель задачи имеет следующий вид.
Минимизировать целевую функцию:
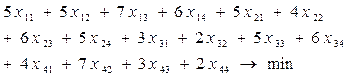(4.12),
при ограничениях
по имеющейся потребности:
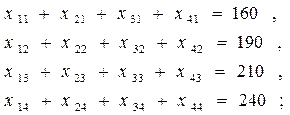(4.13),
по имеющимся запасам:
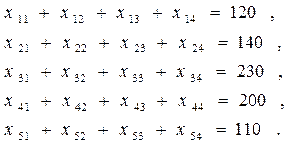(4.14),
Все переменные неотрицательны.
Полученное решение, а также модель задачи представлены ниже (рис. 4.1).
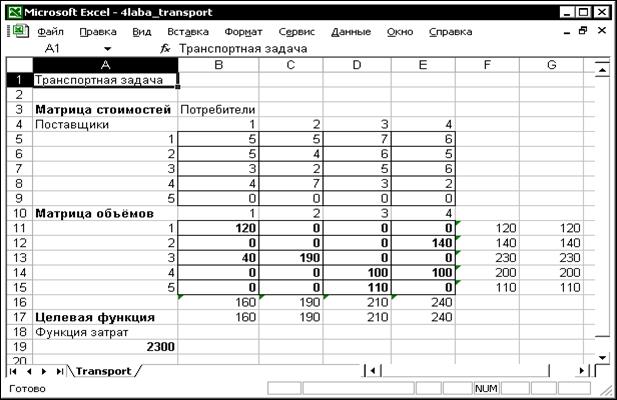Рис. 4.1 Решение транспортной задачи средствами MS Excel
Как видим, получен несколько иной план перевозок, однако при тех же минимальных затратах 2300. В качестве самостоятельного задания рекомендуется проверить данный план перевозок на оптимальность, используя метод потенциалов.
Варианты для выполнения лабораторной работы №4
Задание
В пределах некоторого экономического района имеются четыре карьера, производящих нерудное сырье, и четыре пункта потребления (заводы железобетонных изделий, строительные и дорожные организации и т.п.). Требуется определить объем перевозок готовой продукции от j -го карьера i-му потребителю.
При этом известны нужды каждого потребителя в нерудном сырье, объемы производства на каждом карьере и стоимость перевозки 1м3 продукции с j - го карьера i - му потребителю.
Подставьте необходимые значения переменных для соответствующих вариантов выполнения задания из таблицы 4.18. Предварительно, определите в соответствии со своим вариантом по таблице 4.17 номера поставщиков и потребителей для таблицы 4.18.
Решите задачу с помощью симплекс-метода в Excel, методом северо-западного угла, методом двойного предпочтения, методом наименьших стоимостей. Оптимизируйте все неоптимальные решения.
Таблица 4.17
| Номера потребителей Номера поставщиков | 1-4 | 2-5 | 3-6 | 4-7 | 5-8 | 6-9 | 7-10 | 8-11 | 9-12 | 10-13 |
| 1-4 | 1[6] | |||||||||
| 2-5 | ||||||||||
| 3-6 | ||||||||||
| 4-7 | ||||||||||
| 5-8 | ||||||||||
| 6-9 | ||||||||||
| 7-10 | ||||||||||
| 8-11 | ||||||||||
| 9-12 | ||||||||||
| 10-13 |
Таблица 4.18
| Постав-щик № | Потребитель № | Запасы груза | ||||||||||||
| 2[7] | ||||||||||||||
| Потреб-ность в грузе |
4.Рекомендуемая литература
1. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. Учеб. пособие для студ. Втузов. – 2-е изд., стер. – М.: Высшая школа, 2001. – С. 70-80.
2. Резниченко С.С., Ашихмин А.А. Математические методы и моделирование в горной промышленности. – М.: МГГУ, 1997. – С.114-139.
3. Резниченко С.С., Ашихмин А.А., Подольский М.П., Стрельцова Т.В. Сборник конкретных ситуаций и задач для самостоятельной работы по курсу «Математическое программирование и моделирование». – М.:МГГУ, 1988. – С.22-28.
