для нескольких значений массы самолета (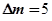 кг).
кг).
Для расчета траектории крейсерского полета к двум основным уравнениям необходимо добавить уравнение расхода массы топлива
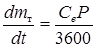 или
или 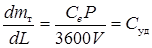 ,
,
где 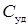 - коэффициент удельной дальности. Магистральные самолеты имеют обычно большое аэродинамическое качество (
- коэффициент удельной дальности. Магистральные самолеты имеют обычно большое аэродинамическое качество (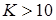 ), поэтому значение тяги двигателя в горизонтальном полете можно получить из приближенной формулы
), поэтому значение тяги двигателя в горизонтальном полете можно получить из приближенной формулы
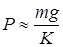 ,
,
что позволяет получить известную аналитическую формулу для дальности полета
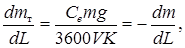
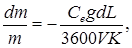
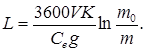
Однако, эта формула справедлива, если в процессе полета остаются постоянными скорость полета 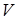 , аэродинамическое качество
, аэродинамическое качество 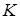 и удельный расход топлива
и удельный расход топлива 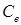 , который для турбореактивных двигателей зависит от высоты полета
, который для турбореактивных двигателей зависит от высоты полета 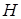 , числа
, числа 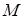 и степени дросселирования двигателя, коэффициента.
и степени дросселирования двигателя, коэффициента. 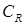 . В результате возникает задача определения наиболее выгодных условий полета при каждом значении массы самолета, обеспечивающих максимальную дальность полета при заданном запасе топлива, что эквивалентно минимизации коэффициента удельной дальности
. В результате возникает задача определения наиболее выгодных условий полета при каждом значении массы самолета, обеспечивающих максимальную дальность полета при заданном запасе топлива, что эквивалентно минимизации коэффициента удельной дальности 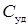 в каждой точке траектории или в нескольких точках, в зависимости от отношения запаса топлива к конечной массе самолета. Для рассматриваемого самолета целесообразно выбрать
в каждой точке траектории или в нескольких точках, в зависимости от отношения запаса топлива к конечной массе самолета. Для рассматриваемого самолета целесообразно выбрать 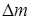 =5 кг. Эта задача может быть решена с помощью метода условной оптимизации, который позволяет найти минимум функции при наличии условий связи, заданных в виде равенств. Таким образом, необходимо найти минимум функции
=5 кг. Эта задача может быть решена с помощью метода условной оптимизации, который позволяет найти минимум функции при наличии условий связи, заданных в виде равенств. Таким образом, необходимо найти минимум функции
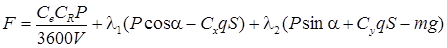 ,
,
где 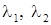 - множители Лагранжа. Необходимым условием минимума функции
- множители Лагранжа. Необходимым условием минимума функции 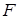 является равенство нулю ее первых производных по всем неизвестным параметрам, включая множители Лагранжа (
является равенство нулю ее первых производных по всем неизвестным параметрам, включая множители Лагранжа (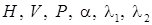 ), причем производные по множителям Лагранжа совпадают с соотношениями, справедливыми для установившегося горизонтального полета. Следует отметить, что вычисление производных, например
), причем производные по множителям Лагранжа совпадают с соотношениями, справедливыми для установившегося горизонтального полета. Следует отметить, что вычисление производных, например 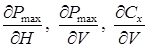 и т. д., может вызвать определенные трудности, поскольку функции
и т. д., может вызвать определенные трудности, поскольку функции 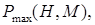
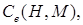
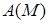 ,
, 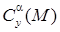 , заданы таблично. В результате получится система из 6 нелинейных алгебраических уравнений с 6-ю неизвестными, которая может быть решена с использованием численных методов оптимизации.
, заданы таблично. В результате получится система из 6 нелинейных алгебраических уравнений с 6-ю неизвестными, которая может быть решена с использованием численных методов оптимизации.
Другой более простой путь заключается в использовании прямого метода, т. е. в поиске для каждого значения высоты полета 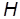 , наиболее выгодных условий горизонтального полета, обеспечивающих минимум функции
, наиболее выгодных условий горизонтального полета, обеспечивающих минимум функции 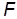 , при этом множители Лагранжа вычислять не нужно, поскольку выражения в скобках будут равны нулю, а сама функция
, при этом множители Лагранжа вычислять не нужно, поскольку выражения в скобках будут равны нулю, а сама функция 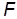 будет совпадать с коэффициентом удельной дальности
будет совпадать с коэффициентом удельной дальности 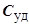 , который можно представить в следующем виде:
, который можно представить в следующем виде:
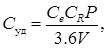 (кг топлива/км).
(кг топлива/км).
Таким образом, задача сводится к поиску высоты полета, на которой достигается наименьшее из минимальных коэффициентов удельной дальности, вычисленных для различных значений высоты полета 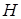 . При выборе начального значения высоты полета, следует иметь в виду, что область возможных режимов полета построена для среднего значения массы самолета, причем наибольшая высота полета получена для
. При выборе начального значения высоты полета, следует иметь в виду, что область возможных режимов полета построена для среднего значения массы самолета, причем наибольшая высота полета получена для 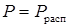 , т. е. при
, т. е. при 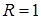 .
.
Результаты расчетов для первого варианта приведены на рис. 2 и в табл. 6. Хорошо видно, что полет должен происходить при 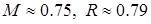 , при этом большее значение массы требует использования большей тяги двигателей и уменьшение массы самолета на 5 кг позволяет увеличить высоту полета примерно на 400 м.
, при этом большее значение массы требует использования большей тяги двигателей и уменьшение массы самолета на 5 кг позволяет увеличить высоту полета примерно на 400 м.
Таблица 6. Крейсерский полет.
| m, кг | 80.000 | 85.000 | 90.000 | 95.000 | 100.000 |
| H, км | 11.448 | 10.933 | 10.521 | 10.111 | 9.712 |
| V, м/с | 221.176 | 221.519 | 222.980 | 224.259 | 224.877 |
| q, кн/м2 | 8.321 | 9.028 | 9.634 | 10.257 | 10.832 |
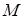
| 0.750 | 0.750 | 0.750 | 0.750 | 0.748 |
| a° | 4.242 | 4.134 | 4.092 | 4.051 | 4.042 |
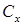
| 0.036 | 0.035 | 0.034 | 0.034 | 0.034 |
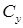
| 0.559 | 0.547 | 0.543 | 0.538 | 0.536 |
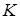
| 15.678 | 15.728 | 15.737 | 15.761 | 15.810 |
| P, кн | 49.941 | 52.893 | 55.971 | 58.992 | 61.905 |
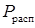 , кн , кн
| 62.536 | 67.363 | 71.220 | 75.062 | 78.767 |
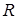
| 0.799 | 0.785 | 0.786 | 0.786 | 0.786 |
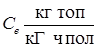
| 0.605 | 0.608 | 0.610 | 0.612 | 0.613 |
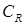
| 0.904 | 0.906 | 0.906 | 0.906 | 0.906 |
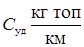
| 3.497 | 3.724 | 3.929 | 4.132 | 4.333 |
 2015-05-13
2015-05-13 622
622







