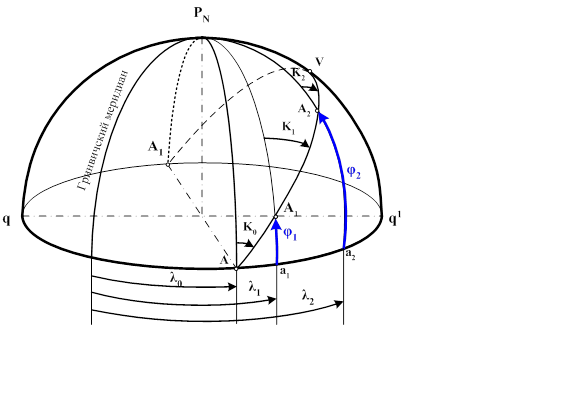
На шаре линией кратчайшего расстояния является дуга большого круга (ДБК), которую называют ортодромией. В переводе с греческого языка ортос - прямой, дромос - проход, бег.
Через две произвольные точки шара В1 и В2 можно провести только одну ортодромию, так как плоскость ДБК проведена через три точки: В1, В2 и центр Земли.
Треугольник МВ1b1 прямоугольный, так как меридиан пересекается с экватором в точке M под углом 90°. Поскольку стороны этого треугольника являются дугами окружностей больших кругов, то решают его, используя формулы сферической тригонометрии.
Применяя к треугольнику МВ1b1 формулу тангенса катета прямоугольного сферического треугольника, можно записать
tg φ1 = sin(λ1 - λ0) tg(90-K0)
Это выражение справедливо для любой точки ортодромии, поэтому полученное выражение является ее уравнением:
tg φ = sin(λ1 - λ0) ctgK0
где λ0 и K0 — параметры ДБК (λ0 — долгота пересечения ДБК с экватором, Ko — направление ДБК в этой точке).
ДБК достигает максимальной широты в точке V, которая называется "вертекс". Вертексов два: один в северном полушарии (виден на рисунке), другой — в южном.
Координаты вертекса:
φV = 900 - K0 λV = λ0 +900
Проанализируем полученные выражения с целью определения свойств ортодромии. Свойства ортодромии.
1. Из выражения λV = λ0 +900 и рисyнка видно, что меридиан вертекса является плоскостью симметрии ортодромии. То есть ортодромия пересекает каждый меридиан два раза в долготах: λi и λi'= 2λν — λi
2. Из выражения φV = 900 - K0:
если Ko = 90° (270°), то ортодромия совпадает с экватором, если Ko = 0° (180°), то ортодромия совпадает с меридианом.
3. Из выражения tg φ = sin(λ1 - λ0) ctgK0 видно, что если неоднократно изменять долготу λ на 360° (предположим, что совершается кругосветное путешествие по ортодромии), то правая часть уравнения не изменяется. Не изменится и левая часть — широта постоянна. Значит ортодромия пересекает каждый меридиан каждый раз в одной и той же точке. Ортодромия — замкнутая кривая.
4. Судоводителей особо интересует направление ортодромии, то есть угол K, под которым ортодромия пересекает меридианы (курс ортодромии). Видно, что K = f(φi,λi), т. е. курс ДБК зависит от координат точек A1 и A2. Следовательно, ортодромия пересекает все меридианы под различными углами:
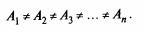
Разность углов, под которыми ортодромия пересекает меридианы двух точек, называется схождением (сближением) меридианов и обозначается буквой γ (гамма) греческого алфавита:
γ = А2 – А1
 2015-05-13
2015-05-13 2617
2617








