§1.Множества. Определения.
Понятие множества – фундаментальное понятие математики, поэтому невозможно дать явное его определение, обычно термин «множество» лишь понимают на примере. Так, перечисляя: картофель, капуста, морковь и т. д, можно назвать их одним словом «овощи». Итак, множество – это совокупность объектов, рассматриваемых как единое целое, т.е, новый объект.
Имеется два существенно различных способа задания множества. Первый способ – описание: А – множество натуральных чисел, не превосходящих 5. Второй способ – перечисление: А =(1,2,3,4,5). Тот факт, что объект х принадлежит множеству А обозначается: хÎА; и хÏА означает, что х не является элементом множества А.
Заметим, что объект а и множество (а) – различные объекты. Если аÎ(а) – истинное утверждение, то (а)Îа – ложное. Перечисление годится только в том случае, когда А содержит конечное и небольшое количество элементов. Описательный способ состоит в указании общего свойства объектов, составляющих данное множество. Оно имеет вид А={х/P(x)}, где P(x) – формула или высказывание, характеризующие в точности все элементы данного множества (принцип абстракции Кантора).
Используются специальные символы для обозначения некоторых множеств: N,Q,R,C,Z,Q+,R+,Z+ - обозначение соответственно множеств, натуральных, рациональных, действительных, комплексных целых чисел. Знак «+» означает, что рассматриваются только положительны числа.
Примеры:
a) A={ xÎR| x>10} – действительные числа, больше 10
b) A={2n|nÎZ} – четные целые числа
c) A=(- 2,+¥) – действительные числа, больше, чем -2
d) A=(- 2,4] – интервал, содержащий 4 и не содержащий -2
e) Æ={x|x¹x} – пустое множество, не содержащие ни одного элемента.
Два множества считаются равными тогда и только тогда, когда они состоят из одних и тех же элементов (принцип объёмности).
Множество B называется подмножеством множества A (обозначается B£A) тогда и только тогда, когда каждый элемент множества B принадлежит множеству A. Отношение между множеством A и любым его подмножеством называется включением. Отметим важные свойства понятия включения:
1. A£B. Любое другое подмножество B, отличное от A называется собственным и обозначается B<A, при этом Æ является подмножеством любого множества.
2. A=B«A£B и B£A (симметричность)
3. Если A£B и B£C, то A£C (транзитивность)
Если все рассматриваемые в данной задаче множества являются подмножествами некоторого множества u, то это множество u называют универсальным, в элементарной арифметике универсальным множеством служит Z –множеством целых чисел, в аналитической геометрии на плоскости – множество (x,y) упорядоченных пар действительных чисел и т.д.
Пусть u= (a1,..,an). Число элементов множества u назовем его мощностью и обозначим | u|=n. Множество всех подмножеств множества u называется степень -множеством множества u и обозначается (P(u).
Теорема. Мощность степень-множества |(P(u)| равна 2½u½.
Доказательство. Пусть u=(a1,..an) и B£u. Поставим в соответствие подмножеству B последовательность длинны n из нулей и единиц по следующему правилу: если aiÎB, то на i-ом месте в последовательности стоит 1, а если aiÏB, то 0. Например, пустому множеству соответствует последовательность из одних нулей, а самому u – из одних единиц. Так как число всех последовательностей равно 2n, то это доказывает теорему.
§2 Операции на множествами.
Определим операции, позволяющие из двух подмножеств строить новое.
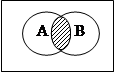
1. Объединение (сумма). Обозначается AÈB, соответствует союзу «или» (в неисключающим смысле).
AÈB={x|xÎA или xÎB}
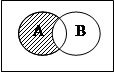
2. Пересечение (произведение). Обозначается AÇB, соответствует союзу «u».
AÇB={x|xÎA, xÎB}
3. Разность. Обозначается A\B. Это множество тех элементов множества A, которые не принадлежат множеству B.
A\B={xÎA| xÏB}
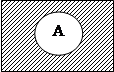
4. Дополнение. Обозначается ` A=u \ A
Для лучшего понимания этих операций используют диаграммы Эйлера – Венна. Универсальное множество изображается в виде прямоугольника, а подмножества в виде кругов.
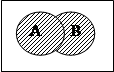 |  |  |  | ||||||||||||
|
|
|
| ||||||||||||
Теорема. Для любых подмножеств A, B, C универсального множества u справедливы следующие равенства
1. AÈB = BÈA 1’ AÇB=BÇA
2. AÈ(BÈC)=(AÈB)ÈC 2¢ AÇ(BÇC)=(AÇB)ÇC
3. AÈ(BÇC)=(AÈB)Ç(AÈC) 3¢ AÇ(BÈC)=(AÇB)È(AÇC)
4. AÈ(AÇB)=A 4¢AÇ(AÈB)=A
5. 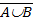 =
=  Ç
Ç 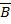 5¢
5¢ 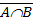 =
=  È
È 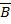
6. AÈA=A 6¢AÇA=A
7. AÈ  =u 7¢AÇ
=u 7¢AÇ  =Æ
=Æ
8. AÈu=u 8¢AÇÆ=Æ
9. AÈÆ=A 9¢AÇu=A
10 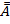 =A
=A
Эти равенства носят названия: 1,1¢ - коммутативность сложения и умножения; 2,2¢ - ассоциативность сложение и умножения; 3,3¢ - дистрибутивность 4,4¢-законы поглощения, 5,5¢-законы де Моргана; 6,6¢ идемпотентность; 10 – закон снятия двойного отрицания.
Докажем, например, равенство 5.
Пусть xÎ 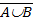 , значит, xÏAÈB, т.е. xÏA и xÏB, xÎ
, значит, xÏAÈB, т.е. xÏA и xÏB, xÎ 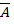 и xÎ
и xÎ 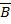 , откуда xÎ
, откуда xÎ  Ç
Ç 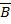 . Обратно. Пусть xÎ
. Обратно. Пусть xÎ  Ç
Ç 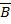 , значит, xÎ
, значит, xÎ 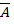 и xÎ
и xÎ 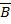 , т.е. xÏA и xÏB, т.е. xÏAÈB т.е. xÎ
, т.е. xÏA и xÏB, т.е. xÏAÈB т.е. xÎ 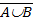 .
.
Заметим, что равенства левого столбца получаются из равенства правого столбца заменой символа Ç («крышки») на символ È («чашки») и наоборот. Символ пустого множества Æ заменяется символом универсального множества u и наоборот.
§3 Прямое произведение множеств.
Пусть A, B – два множества. Их прямым (декартовым) произведением называется множество упорядоченных пар AхB=((x,y)| xÎA, yÎB). При этом, если (x,y)=(u,v) то x=u, y=v. Будем называть x первой координатой, а y - второй координатой упорядоченной пары. Аналогично определяются упорядоченные тройки (x,y,z) и т.д. Вообще, пусть A1,A2,..Ak – множества. Тогда их прямым произведением назовем множество упорядоченных последовательностей (x1,x2,..xk) таких, что xiÎAi, i=1,2…k.
В частности, если A=B, то AхA будем обозначать A2, и аналогично, если Ai=A, то A1хA2.. хAk=Ak.
Замечание 1. Если R – множество действительных чисел, т.е. точек числовой прямой, то R2 и R3 –это соответственно множества точек плоскости и пространства.
Замечание 2. Пусть E – множество, состоящие из двух элементов 0 и 1. Тогда En – множество последовательностей из n элементов, каждый из которых 0 либо 1.
Теорема. Пусть A={a1,..an}, B={b1,.. bm}, т.е. |A|=n |B|=m. Тогда прямое произведение AхB содержит n х m элементов. |AхB|=|A||B|
Доказательство. Элементы множества AхB запишем в виде таблицы:
(a1,b1) (a1,b2) (a1,bm)
(a2,b1) (a2,b2) (a2,bm)
……. …….. ………
(an,b1) (an,b2) (an,bm)
Откуда следует утверждение теоремы.
Следствие 1. |A1хA2х..Ak|=|A1|х|A2|..|Ak|
Следствие 2. |En|=2n
Задачи.
В следующих задачах нужно доказать равенство множеств:
1. A={y=x2| xÎR, x¹0} и R+
Решение. Пусть yÎA, y=x2, x¹0, т.е. yÎR+
Обратно. Пусть yÎR+, тогда y=( 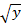 )2=x2, где x=
)2=x2, где x= 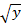 , xÎR+, x¹0, т.е. yÎA.
, xÎR+, x¹0, т.е. yÎA.
2. A={6n| nÎZ}, B={3m| mÎZ}, C={2k| kÎZ}; A=BÇC
Решение. Пусть xÎA; x=6n, nÎZ. Тогда x=3m, m=2n и xÎB. Аналогично, x=2k, k=3n и xÎC. Итак A£BÇC. Обратно. Пусть xÎBÇC. Тогда x=3m=2k. 3m делится на 2, и поскольку 3 и 2 взаимно просты, то m=2n. Значит x=3m=3*2n=6n. xÎA
3. A={2x| xÎQ} и Q
4. A={2x| xÎR} и R+
5. A={lgx| xÎR+} и R
6. A={30n| nÎZ}, B={5m| mÎZ}, C={3l| lÎZ}, D={2k| kÎZ}
A=BÇCÇD
7 (AÇBÇC)È(  ÇBÇC)È
ÇBÇC)È 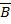 È
È 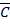 =u
=u
Решение (AÇBÇC)È(  ÇBÇC)=(AÈ
ÇBÇC)=(AÈ  )Ç(BÇC)=uÇ(BÇC)=BÇC
)Ç(BÇC)=uÇ(BÇC)=BÇC
(BÇC)È( 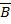 È
È 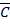 )=(BÇC)È(
)=(BÇC)È( 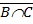 )=u
)=u
8 (AÇBÇX)È(AÇBÇCÇXÇY)È(AÇXÇ  )=AÇBÇX
)=AÇBÇX
9 (AÇBÇCÇ 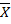 )È(
)È(  ÇC)È(
ÇC)È( 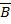 ÇC)È(CÇX)=C
ÇC)È(CÇX)=C
10 [(AÇB)È(AÇC)È(  Ç
Ç 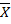 ÇY)]Ç
ÇY)]Ç 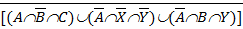 =
=
=(AÇB)È(  Ç
Ç 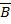 Ç
Ç 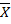 ÇY)
ÇY)
11 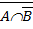 ÈB=
ÈB=  ÈB
ÈB
В следующих задачах надо описать указанные множества.
В заданиях 12, 13, 14 универсальным является множествоZ.
12 Пусть A={2n| nÎZ}, B={2n-1| nÎZ}, C={xÎZ| x<5}
Описать множества  ,
, 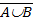 ,
, 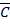 , A\
, A\ 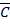 , C\(AÈB)
, C\(AÈB)
Решение A – множество четных, а B – нечетных целых чисел. AÈB=Z, значит  =B,
=B, 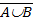 =Æ
=Æ 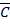 ={xÎZ| x³5}. Тогда A\
={xÎZ| x³5}. Тогда A\ 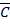 – это множество четных чисел меньше 5: и т.к. AÈB=Z, то C\(AÈB)=Æ.
– это множество четных чисел меньше 5: и т.к. AÈB=Z, то C\(AÈB)=Æ.
13 A={xÎZ+| x=2y, yÎZ}, B={xÎZ+| x=2y+1, yÎZ}, C={3y| yÎZ+}
Описать множества AÇB, BÇC, B\C.
14 Описать множества 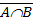 , AÈ
, AÈ 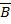 , AÇBÇC из задачи 13.
, AÇBÇC из задачи 13.
15 Доказать каждое из следующих утверждений для произвольных множеств A, B, C:
a) Если A≤B и B≤C, то A≤C
b) Если A≤B и B<C, то A<C
c) Если A<B и B≤C, то A<C
d) Если A<B и B<C, то A<C
Решение. Докажем, например, b) Рассмотрим случай A=B. т.к. B<C, то существует xÎC и xÏB=A, т.е. A<C. Пусть теперь A<B, значит, существует xÎB и xÏA. Поскольку B<C, то xÎC, т.е. опять A<C.
16 Какие из следующих утверждений верны для всех множеств A, B, C?
a) Если AÏB и BÏC, то AÏC
Неверно. Например: A=1, B={0,2,3}, C={1,3,4}
b) Если A¹B, B¹C, то A¹C. Неверно. Например, если A=C¹B
c) Если AÎB и неверно, что B≤C, то AÏC
 Неверно утверждение как показывает следующий рисунок
Неверно утверждение как показывает следующий рисунок
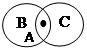 |
A – элемент пересечения BÇC
d) Если A<C и B≤C, то неверно, что C≤A.
Верное утверждение. На основании 15с A–собственное подмножество C, т.е. существует xÎC и xÏA.
e) Если A≤B и BÎC, то AÎC. Неверное утверждение. Пусть A={1}, B={1,2}, C={{1,2},3}
Тесты по теме «Множества».
Тест №1.
Задание 1.
ЕслиA=(-¥, -2), B=(-3,+¥), то AÈB:
a) (-3,-2)
b) (-3,-2]
c)
d) 
 (-¥,-3)È(-2,+¥)
(-¥,-3)È(-2,+¥)


|
|


 Правильный ответ c):
Правильный ответ c): Задание 2.
Если A – множество четных чисел, B – множество чисел кратных 6, то  ÇB есть
ÇB есть
a) Множество A
b) Множество B
c) Æ
d) Множество чисел кратных 12.
Правильный ответ c), поскольку  – множество нечетных чисел.
– множество нечетных чисел.
Задание 3.
AÇ( ÈB)=
ÈB)=
a) AÈB
b) AÇB
c) Æ
d)  ÈB
ÈB
Правильный ответ b): AÇ( ÈB)=(AÇ
ÈB)=(AÇ  )È(AÇB)=ÆÈ(AÇB)=AÇB
)È(AÇB)=ÆÈ(AÇB)=AÇB
Задание 4.
Если A≤B, то (несколько ответов).
a) AÈB=B
b) AÈB=A
c) AÇB=A
d)  ³
³ 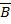
Правильный ответ a),c),d). Проверим d). Пусть xÎ 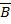 , xÏB, значит, xÏA, т.е. xÎ
, xÏB, значит, xÏA, т.е. xÎ 
Задание 5.
Декартовым произведением A х B множества A={-1,1} и B={1,5} является множество:
a) (-1,5)
b) (-1,1),(1,5)
c) (-1,1), (-1,5), (1,1), (1,5)
d) (1,-1), (5,-1), (1,1), (5,1)
Правильный ответ c)
Тест №2.
Задание 1.
Если C=(-1,1)È(2,+¥), то 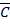
a) (1,2)
b) (-¥,-1)È(1,2)
c) (-¥,-1]È[1,2]
d) (-¥,+¥)
Правильный ответ c).
Задание 2.
Если A – множество квадратов, B–множество ромбов, то AÇB есть:
a) Множество A
b) Множество B
c) Æ
d) Множество прямоугольников
Правильный ответ a)
Задание 3.
(A\B)ÈB=
a) A
b) B
c) AÈB
d) AÇB
Правильный ответ с), т.к. (A\B) ÈB=(AÇ 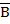 )ÈB=(AÈB) Ç(
)ÈB=(AÈB) Ç(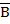 ÈB)=(AÈB) Çu =AÈB
ÈB)=(AÈB) Çu =AÈB
Задание 4.
Если AÇB=Æ, то (несколько ответов)
a) A≤ 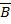
b) B≤ 
c) AÈB=u
d) BÈ(AÇB)=B
Правильные ответы: a),b),d)
Покажем для a). ПустьxÎA, т.к. AÇB=Æ, то xÏB, т.е. xÎ 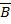
Задание 5.
(A х B)Ç(C х D)=
a) (AÇC) х (BÇD)
b) (A х C)È(A х D)È(B х C)È(B х D)
c) (A х C)Ç(B х D)
d) (A х C)È(B х D)
Правильный ответ a).
Пусть (x, y)Î(A х B)Ç(C х D), т.е. xÎA и xÎC; yÎB и yÎD т.е. xÎAÇC, yÎ(BÇD).И обратно, если (x, y)Î(AÇC)х(BÇD), то xÎAÇC, yÎBÇD. Значит, (x, y)Î(AхB)Ç(CхD)
§4 Отношение. Определения.
В курсе аналитической геометрии линия на плоскости определялась как г.м.т. (геометрическое место точек), координаты которой удовлетворяют некоторому отношению. Это отношение между координатами точки могло выражаться как словесно, так и формулой. Например, окружность может быть определена как г.м.т, расстояние которых от фиксированной точки есть постоянная величина, либо г.м.т, координаты которых удовлетворят равенству (x-a)2+(y-b)2=r2. Каждую точку плоскости (x,y) мы рассматривали как элемент прямого произведения R х R. Тогда линия – это некоторое множество R х R, задаваемое высказыванием (формулой P(x, y))
Пусть теперь A и B–произвольные множества. Отношением из A в B (бинарным отношением) назовем подмножество прямого произведения A х B. Символически это обозначается так r={(x,y)ÎA х B|P(x,y)}
Мы считаем, что выражение (x,y)Îr и xry взаимозаменяемые. При этом для некоторых специальных отношений: равенства, неравенства, тождества, включения, приняты специальные обозначения: x=y, x≤y, xºy, xÎy. Естественным образом определение обобщается на случай n - арного отношения:
r={(x1,..,xn)ÎA1x...xAn| P(x1,..xn)}
Если множества A и B совпадают, то rÎA х A называется отношением, заданным на множестве элементов множества A.
Примеры:
1. Пусть A – множество женщин, B–множество мужчин, r - отношение материнства, (x,y)Îr означает x мать y.
2. Пусть A – множество студентов, r - отношение соседства, xry означает x живет в одном общежитии с y.
3. Пусть A=R, r -отношение сравнения, xry означает x³y.
§5Области определения и значений. График отношения.
Областью определения r (Dr) называется множество всех первых координат, а областью значений (Rr) –множество всех вторых координат
Если rÎA х B, то
Dr={xÎA| существуют yÎB, такой, что (x,y)Îr}
Rr={yÎB| существуют xÎA, такой, что (x,y)Îr}
Если r≤R х R, то графиком отношения r называется совокупность всех точек (x,y) плоскости, для которых (x,y)Îr. В этом случае D есть проекция графика на ось ox, а Rr - проекция на ось oy.
§6 Основное свойства отношений.
Пусть r - отношение на множество элементов A. Отношение r называется:
1 Рефлексивным, если для всех xÎA (x,x)Îr.
2 Антирефлексивным, если для всех xÎA неверно, что (x,x)Îr.
3 Симметричным, если из того, что (x,y)Îr вытекает, что (y,x)Îr.
4 Антисимметричным, если из того, что (x,y)Îr и (y,x)Îr следует, что x=y.
Антисимметричность можно определить так: если (x,y)Îr и x¹y, то (y,x)Ïr. Заметим, что единственным отношением, которое одновременно симметрично и антисимметрично будет отношение равенства.
5 Транзитивность: если (x,y)Îr и (y,z)Îr, то и (x,z)Îr.
Замечание.
Если r - отношение на множестве действительных чисел, то свойства отношения r можно интерпретировать геометрически. Рефлексивность означает, что вся биссектриса x=y принадлежит графику, антирефлексивность – ни одна точка биссектрисы не принадлежит графику. Симметричность означает, что график симметричен относительно биссектрисы, антисимметричность означает, что если точка, принадлежащия графику, не лежит на биссектрисе, то симметричная относительно биссектрисы точка, не принадлежит графику.
Задачи.
1 Для отношения r={(x,y)ÎR х R| x2+y2³1} построить график, найти область определения и значений и выяснить, какими свойствами оно обладает.

|
|












 Графиком отношения r будет внешность круга радиуса 1, включай окружность. Dr=Rr=R. (проекции на оси oxи oy) Отношение r не является ни рефлексивным, ни антирефлексивным (есть точки, принадлежащие биссектрисе и не принадлежащие ей. (1,1)Îr, но ((0,0)Ïr). Отношение r является симметричным, поскольку если x2+y2³1, то y2+x2³1. Так как r не является отношением равенства, то оно не антисимметрично: (1,2)Îr и (2,1)Îr, но 1¹2.
Графиком отношения r будет внешность круга радиуса 1, включай окружность. Dr=Rr=R. (проекции на оси oxи oy) Отношение r не является ни рефлексивным, ни антирефлексивным (есть точки, принадлежащие биссектрисе и не принадлежащие ей. (1,1)Îr, но ((0,0)Ïr). Отношение r является симметричным, поскольку если x2+y2³1, то y2+x2³1. Так как r не является отношением равенства, то оно не антисимметрично: (1,2)Îr и (2,1)Îr, но 1¹2. Отношение r не является транзитивным, как показывает пример:
x=0=z, y=1; (0,1)Îr т.к. 0+1³1, (1,0)Îr, т.к. 1+0³1, но (0,0)Ïr, т.к. 0+0<1.
2 r={(x,y)ÎR2½|x-y|≤1}








|
|



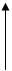

 |x-y|≤1 означает, что -1≤y-x≤1, т.е. y≤x+1 и y³x-1. Графиком является полоса. Dr=Rr=R. Отношение r рефлексивно т.к. |x-x|=0<1, и симметрично, потому что |x-y|=|y-x|. Оно не тразитивно. Если x=0, y=1, z=2, то |0-1|≤1, |1-2|≤1, но |0-2|>1.
|x-y|≤1 означает, что -1≤y-x≤1, т.е. y≤x+1 и y³x-1. Графиком является полоса. Dr=Rr=R. Отношение r рефлексивно т.к. |x-x|=0<1, и симметрично, потому что |x-y|=|y-x|. Оно не тразитивно. Если x=0, y=1, z=2, то |0-1|≤1, |1-2|≤1, но |0-2|>1. 3 



 r={(x, y)ÎR2| (x-1)(y-1)³0}
r={(x, y)ÎR2| (x-1)(y-1)³0} 



 График отношения дан на чертеже. Dr=Rr=R
График отношения дан на чертеже. Dr=Rr=R Отношение рефлексивно, симметрично, но не транзитивно. Еслиx=2, y=1, z=0, то (2-1)(1-1)³0, (1-1)(0-1)³0, но (2-1)(0-1)=-1<0.
4 r={(x,y)ÎR2½|x-y|=0}
Условие |x-y|=0 означает, что x=y. Отношение r является рефлексивным, симметричным и транзитивным. График – биссектриса.
5 r={(x,y)ÎR2| x2+y2³2xy}
x2+y2³2xy означает (x-y)2³0. График – вся плоскость. Отношение r рефлексивно, симметрично и транзитивно.
§7 Отношение эквивалентности.
Отношение r заданное но множестве элементов из множества A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Примеры:
1 Отношение равенства x=y
2 Отношение, заданное на множестве матриц ArB«ранг A= рангу B
3 Отношение, заданное на множестве матриц. ArB«det A= det B
4 Отношение равносильности система линейных уравнений.
5 Отношение «соседства»: x ry«x и y живут в одном доме.
6 Отношение, заданное на множестве прямых на плоскости: l1rl2 «прямые l1 и l2 или совпадают или не пресекаются.
7 Отношение подобия треугольников.
8 Сравнение по модулю целого числа n. Обозначается xºy(modn) «(x-y) делится нацело на n, где x и y –целые числа. Рефлексивность и симметричность очевидны. Докажем транзитивность. Докажем транзитивность. Пусть x-y=nk1, y-z=nk2. Тогда (x-y)+(y-z)=n(k1+k2). Здесь k1 и k2 – целые числа.
9 r: |Z1|=|Z2|. Z1и Z2 – комплексные числа.
10 Пусть r -отношение, на множестве пар целых чисел (x,y), причем y¹0:
(x,y)r(u,v)«xv=yu
Докажем транзитивнось. Пусть (x, y)r(u v) и (uv)r(ab). Покажем, что (x,y) r (a,b). Поскольку xv=yu и ub=va, то перемножая, получим (xb) и uv=ya(uv). Если u¹0, то поскольку u¹0, то uv¹0, и xb=ya.
Пусть u=0, тогда xv =0, но v¹0, значит, x =0 и xb =0. С другой стороны, ub =0, т.е. va =0, и значит,a=0, т.е. ya =0. Поэтому xb=ya, и опять (x,y) r (a,b).
Замечание. Если r -отношение эквивалентности, то аналогично отношению сравнению по модулю n вместо xry будем обозначать x ºy(r).
§8 Классы эквивалентности.
Пусть r - отношение эквивалентности на множестве A. Классом эквивалентности элемента xÎA будем называть все те yÎA, для которых yºx(r) и обозначать [x].
Теорема 1. Классы эквивалентности или не пересекаются или совпадают.
Доказательство. Пусть zÎ[x]Ç[y]. Тогда xºz(r) и zºy(r) следовательноxºy(r) и [x]=[y].
В примере 1 класс эквивалентности содержит 1элемент, в примере 5 – все люди, живущие в одном доме, в примере 8 – все числа, дающие при делении на n один и тот же остаток (всего n классов), в примере 9 геометрическим образом класса эквивалентности является окружность данного радиуса с центром в начале координат.
В примере 10 сопоставим элементу (x,y) рациональную дробь  . Тогда класс эквивалентности для (x,y) – это все рациональные дроби, равные
. Тогда класс эквивалентности для (x,y) – это все рациональные дроби, равные  .
.
§9 Разбиения.
Пусть A – некоторое множество, и Ai, i=1,2… его подмножества, такие, что
ÈAi=A и AiÇAj=Æ если i¹j. Тогда подмножества Ai называют разбиением множества A.
Теорема 2. Отношение эквивалентности, заданное на множестве Aопределяет разбиение этого множества, и обратно, всякое разбиение определяет отношение эквивалентности.
В самом деле, отношение эквивалентности разбивает множество A на классы эквивалентности. Обратно, всякому разбиению можно сопоставить отношение эквивалентности: xry«когда x и y принадлежат одному и тому же подмножеству Ai.
Замечание. Разбиения часто используются при экономических и социологических исследованиях. Например, при анализе доходов население разбивается на несколько возрастных групп. Для более детального исследования рассматриваются и другие факторы: образование, место проживания и.т.д. Чем больше факторов, там больше различныхгрупп. Изучая одного или нескольких представителей одной группы, делаются выводы относительно всей группы. Самым подробным разбиение является такое, когда группа, т.е. класс эквивалентности состоит из одного элемента.
Задачи.
1 Пусть r - отношение эквивалентности на множестве комплексных чисел: r: |Z1|=|Z2|. Какие из следующих утверждений верно?
a) Каждый класс эквивалентности содержит бесконечное число элементов
b) Существуют классы с конечным числом элементов
c) [1+i]=[ 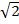 ]
]
d) [i]Ç[-1]=Æ
e) [i]Ç[1-i]=Æ
Ответ: верно b), c), e).
2 Пусть r - отношение эквивалентности на множестве действительных чисел r:
|x|=|y|. Какие из следующих утверждений верны?
a) Каждый класс эквивалентности содержит 2 элемента.
b) Есть классы, содержащие меньше двух элементов.
c) [2,5]Ç[-2,5]=Æ
d) [1]Ç[2]=Æ
Ответ: верно b), d).
3 Пусть r - сравнение по модулю 7. Какие из следующих утверждений верны?
a) [2]=[-2]
b) [2]=[5]
c) [2]=[-5]
d) Каждый класс эквивалентности содержит бесконечное число элементов.
Ответ: верно c), d).
4 r={(x,y)ÎR2| x-yÎZ}
Доказать, что r отношение эквивалентности и описать классы эквивалентности.
Верно ли что:
a) [ 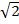 ]=[1,414]
]=[1,414]
b) [1,2]=[-1,2]
c) [0]=[1]
Ответ: классы эквивалентности определяются числом, принадлежащим отрезку [0,1). Верно только c).
§10 Отношение порядка.
Порядком или частичным порядком называется отношение, которое рефлексивно, антисимметрично и транзитивно.
Примеры.
1 Сравнение действительных чисел x≤y.
2 Отношение включения A≤B.
3 Иерархия служащих некоторой фирмы xry «y начальник x.
4 Отношение делимости на множестве натуральных чисел xry«y делится x (нацело). Проверим антисимметричность. y = xn и x=ym, где m, nÎN. Отсюда y=ymn. Т.к. y¹0, то mn=1. Значит, m=n=1, x=y.
Следуя традиции, отношения порядка символически обозначается x≤y. Если x≤y и x¹y, то будем писать x<y. Будем использовать запись y³x и y>x в качестве альтернативы x ≤ y и x < y соответственно. Частичный порядок r называем полным (линейным) порядком, если для любых x и y либо x ≤ y, либо y ≤ x. В приведенных примерах только в примере 1 отношение является линейным порядком.
§11 Наибольший и максимальный, наименьший и минимальный элементы.
Пусть ≤ отношение порядка на множестве A. Элемент yÎA называется наибольшим, если для всех xÎA, x≤y, аналогично y– наименьший, если для всех xÎA, x³y. Элемент y называется максимальным, если из того, что x³y следует x=y. Аналогично y – минимальный если из того, что x≤y следует x=y.
Справедлива следующая:
Теорема 3:
1 Наибольший элемент единственный, а максимальных может быть несколько.
2 Наибольший элемент является максимальным.
3 Для линейного порядка максимальный является наибольшим.
Доказательство. Пусть y1 и y2– наибольшие элементы. Тогда y1≤y2 и y2≤y1, т.е. y1=y2.
Теорема 4.
1 Наименьший элемент единственный, а минимальных может быть несколько.
2 Наименьший элемент является минимальным.
3 Для линейного порядка минимальный является наименьшим. Эта теорема доказывается аналогично (доказать самим).
Задачи:
В задачах 1,2,3 доказать, что отношение r не является частичным порядком, т.к. не выполнена антисимметричность.
1 Отношение r на множестве комплексных чисел. Z1rZ2«|Z1|≤|Z2|
Пример: Z1=1+i
Z2=1-i
2 Отношение r на множестве комплексных чисел. Z1=x1+iy1, Z2=x2+iy2, Z1rZ2«x1≤x2.
Пример: Z1=1+i
Z2=1+2i
3 Отношение r на множестве действительных чисел x1rx2«|x1|≤|x2|.
Пример: x1=1, x2=-1
4 Пусть M={a, b, c}, r - отношение включения на подмножествах {a}, {b},{c}, {a,b}, {a,c}, {b,c}. Показать, что здесь нет наибольшего и наименьшего элементов, но есть 3 максимальных и 3 минимальных.
5 Показать, что добавив Æ, получим наименьший элемент, а если к тому же добавить подмножество {a, b, c}, то и наибольший элемент.
6 Показать, что отношение r в задании 4 не является линейным порядком, но если взять подмножества Æ, {a}, {a, b}, {a, b, c}, - то это будет линейны порядок с наибольшими и наименьшими элементами.
7 r - отношение делимости на множестве {1, 2, 4, 8}. Показать, что это линейный порядок с наибольшим и наименьшим элементами.
8 Показать, что если в задании 7 добавить число 5, что порядок престанет быть линейным. Попрежнему будет наименьший элемент, но не будет наибольшего. Есть ли максимальные элементы и сколько их? Ответ: два- 5 и 8.
9 Отношение r на множестве A={-4, -5, -3, 2, 1}. r: xry«|x|≤|y|. Доказать, что r - линейный порядок и указать наибольший и наименьший элементы. Ответ:
1 – наименьший, -5 – наибольший.
§12 Граф и отношения.
Пусть r отношение, заданное на множестве элементов M={a1, a2,..,an}. Каждому такому соотношению сопоставить геометрическую фигуру, которую назовем графом, или ориентированным графом, по следующему правилу:
Каждому элементу ai сопоставим точку, называемую вершиной. Если airaj, то вершины ai и aj соединим линией (не обязательно прямой), направленной от ai к aj, которую назовем ребром. Будем говорить, что данное ребро инцидентно вершинам ai и aj, а вершины инцидентны этому ребру. Если airai, то возле вершин ai рисуем петлю. Ясно, что существует взаимно однозначное соответствие между отношениями r и ориентированными графами.
§13 Матрица инцидентности вершин графа. Матрица отношения.
Пусть снова r - отношение на множестве M={a1, a2,..,an}. Матрицей отношения r назовем матрицу размерности n х n, у которой в клетке (i, j) стоит 1, если (ai aj)Îr, и 0 (или пустая клетка), если (ai, aj)Ïr.
Эту же матрицу будем рассматривать как матрицу инцидентности (смежности) вершин графа.
Свойства отношения, свойства графа и свойства матрицы отношения.
Рефлексивность означает, что возле каждой вершины петля (соответственно на главной диагонали все 1). Антирефлексивность – нет ни одной петли (на главной диагонали все 0). Симметричность означает, что если вершины соединены ребром, то есть и противоположно ориентированное ребро. (матрица симметрична относительно главной диагонали).
Если r антисимметрично, и есть ребро (ai, aj), то ребра (aj, ai), нет. Соответсвтвенно, если в клетке (i, j), стоит 1 i¹j, то в клетке (j, i) – 0. Транизитивность означает, что если есть ребро (ai, aj) и ребро (aj, ak), то должно быть ребро (ai, ak). Для матриц: если в клетках (i, j) и (j, k) стоит 1, то и в клетке (i, k) должна быть 1.
Замечание. Пусть r - симметричное отношение. Два ребра (ai, aj) и (aj, ai) заменим одним неориентированным ребром. Полученный граф будем называть неориентированным.
§14 Мульти графы и сети.
Начало теории графов было положено работой Эйлера о Кенигсбергских мостах. Графы, которые он изучал, были неориентированными, причем две вершины могли быть соединены несколькими ребрами. Разумеется, подобный граф уже не был геометрическим образом отношения. В матрице инцидентности вершин для него в клетке (i, j) и (j, i) стоит число k, где k – количество ребер, инцидентных вершинам ai и aj. Подобные графы принято называть мультиграфами. При этом мультиграфы могут быть и ориентированными, т.е. в клетках (i, j) и (j, i) стоят разные числа. Граф как ориентированный, так и неориентированный, в котором каждому ребру сопоставлено действительное число, называется сетью.
§15 Специальные графы отношение порядка.
Пусть r - отношение порядка. Сопоставим ему граф, более выпукло характеризующий это порядок.
Ребра такого графа неориентированы, отсутствуют петли. Если x<y, и не существует такого Z, что x<Z<y, то вершина xрасполагается ниже вершины y, и x и y соединены ребром. Такой граф называется специальным графом отношения.
Задачи.
1






 Пусть r - отношение делимости на множестве M={2, 3, 4, 5, 6}. Построить специальный граф этого отношения и указать максимальный и минимальный, наибольший и наименьший элементы.
Пусть r - отношение делимости на множестве M={2, 3, 4, 5, 6}. Построить специальный граф этого отношения и указать максимальный и минимальный, наибольший и наименьший элементы. 
4и 6 – максимальные элементы, 2 и 3 – минимальные. Элемент 5 и максимальный (нет большего) и минимальный (нет меньшего). Наибольшего и наименьшего элементов нет.
2

 Решить задачу, аналогичную задаче 1, если r - отношение сравнения чисел того же множества M. Решение. Это линейный порядок. 6 – наибольший, а 2 – наименьший элементы.
Решить задачу, аналогичную задаче 1, если r - отношение сравнения чисел того же множества M. Решение. Это линейный порядок. 6 – наибольший, а 2 – наименьший элементы.  | ||
 | ||
 | ||
 | ||
 |
3 



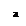

















 Отношение порядка задается графом. Указать наибольший и наименьший, максимальный и минимальный элементы. Решение. Наибольшего нет. Максимальные d и e. Наименьший f.
Отношение порядка задается графом. Указать наибольший и наименьший, максимальный и минимальный элементы. Решение. Наибольшего нет. Максимальные d и e. Наименьший f.
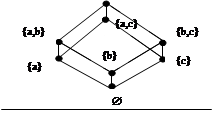
4 M={ {a},{b},{a, b},{a, c}, {b, c}, Æ }. r - отношения включения для подмножеств из M. Построить специальный граф. Указать наибольший, наименьший, максимальный, минимальный элементы.









 Æ - наименьший элемент, наибольшего нет.
Æ - наименьший элемент, наибольшего нет.





 {a, b}, {a, c}, {b, c} – максимальные элементы.
{a, b}, {a, c}, {b, c} – максимальные элементы.
 | |||
 | |||
5 Какое подмножество нужно присоединить к M, чтобы появился наибольший элемент? Ответ: {a, b, c}.
6 
 A={a, b, c} M – множество всех подмножеств множества A. Построить специальный граф отношения включения. Решение.
A={a, b, c} M – множество всех подмножеств множества A. Построить специальный граф отношения включения. Решение.
 |
7 Пусть M={1, 2, 3, 4, 6}. Построить графы для отношения сравнения r1 и отношения делимости r2 на этом множестве.
 |
8 Для этих же отношений задачи 7 построить специальные графы.
 | |||
 | |||
9
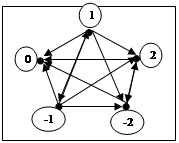 | |||||
 | |||||
| |||||
|
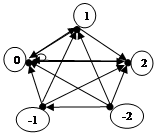
10 Построить специальный граф отношения x≤y задачи 9. Является ли отношение r2 задачи 9 отношением порядка?


 Отношение r2 не является отношением порядка, т.к. 2 делится на -2 и -2 делится на 2, но 2¹-2.
Отношение r2 не является отношением порядка, т.к. 2 делится на -2 и -2 делится на 2, но 2¹-2.  | |||
 | |||
| |||
§16 Функции.
Понятие функции определим в терминах понятия отношения. Отношение r≤ AхB назовем функцией из A в B, если того, что (x, y)Îr и (x, z)Îr следует, что y=z т.е. функции не содержат различных пар с одинаковыми первыми координатами.
Примеры:
1 r={ (1, 2), (1, 5), (2,5)} не является функцией, т.к. различные элементы (1, 2) и (1, 5) имеют одинаковую первую координату.
2 r={ (x, y)ÎR2| y=x2+1} есть функция, т.к. если x=a, то x2+1=a2+1.
3 Отношение { (x2, x)| xÎR} не является функцией, т.к. (4,2)Îr и (4, -2)Îr.
Если f – функция, т.е. (x, y)Î f или xfy, то xесть аргумент функции, a y называют значением функции f, образом элемента x при отображении f. Для обозначения y употребляют различные символы xf, f(x), fx.
Поскольку функции являются множествами, к ним применимо обычное определение равенства множеств: две функции равны тогда и только тогда, когда они состоят из одних и тех же элементов. Другими словами f=g тогда и только, тогда когда Df=Dg и f(x)=g(x), xÎDf=Dg.
Множество всех функций, определенных на X со значением на Y есть подмножество множества всех подмножеств X х Yи обозначается оно yx.
Функция называется взаимно – однозначной, если она переводит различные элементы в различные, т.е. x1¹x2 влечет f(x1)¹f(x2).
Пусть f(x) – взаимно – однозначная функция, Df=X и Rf=Y. Тогда функция f(x) есть множество упорядоченных пар (x, f(x)), где f(x) однозначно определенный элемент множества Y. Каждому yÎY однозначно сопоставляется xÎX такой, что f(x)=y. Ввиду полной симметричности f называют взаимно однозначным соответствием множеств X и Y. Говорят так же, что множества X и Y имеют одинаковую мощность. Ясно, что если одно из них конечно u содержит n элементов, то другое также содержит n элементов.
Задачи:
1 Для данных отношений выяснить, будут ли они функциями, и если это функция, то является ли она взаимно однозначной?
r1={(x, 3x-1)| xÎR}, r2={(x, x2)| xÎR}, r3={(x2, x)| xÎR}, r4={(x, x3)| xÎR}, r5={(x3, x)| xÎR}, r6={(x, lgx)| xÎR+}, r7={(x, y)ÎR х R| x2+y2=1}.
Ответ: r1, r2, r6, r4, r5 – функции, r3 и r7 – нет.
r1, r4, r5, r6, - взаимно однозначны.
2 Установив взаимно – однозначное соответствие, доказать, что следующие множества имеют одинаковую мощность:
a) Множество целых чисел
b) Множество четных чисел
c) Множество нечетных чисел
Ответ: f(n)=2n и f(n)=2n-1
3 Установить взаимно – однозначное соответствие между:
a) Множеством действительных чисел и множеством положительных действительных чисел.
Ответ: x«lg x.
b) Множеством Z+ и множеством Z+xZ+. Указание. Множество элементов Z+xZ+ записать в виде бесконечной матрицы и придумать правило перебора всех элементов Z+xZ+.
4 Для следующих отношений указать область определения и область значений. Выяснить, какие из них функции и какие взаимно – однозначные функции:
r1={(1, 2), (1, 5), (5, 1), (5, 2)}, r2={(1, 6), (6, 1), (2, 3), (3, 2)}, r3={(1, 7), (2, 7), (7, 2), (3, 9), r4={(1, 1), (2, 2), (3, 3), (4, 4)}
r2и r4 – взаимно – однозначные функции.
r3 – функция, но не взаимно – однозначная,r1 не функция.
 2015-05-13
2015-05-13 779
779