Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами, а также электромагнитными волнами, которые генерируются неподвижными и движущимися источниками таких волн. Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
Как уже отмечалось, в классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной.
Сейчас мы сделаем попытку найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [1-3], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы записываются следующим образом:
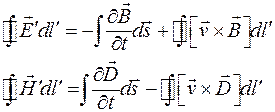 , (1)
, (1)
или
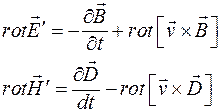 . (2)
. (2)
Для постоянных полей эти соотношения имеет вид:
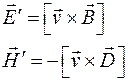 . (3)
. (3)
В этих соотношениях, предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно.
Соотношения (1–3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями 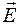 и
и 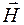 существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях 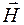 приводит к появлению полей
приводит к появлению полей 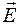 и наоборот. Эти особенности приводят к дополнительным следствиям, которые впервые были рассмотрены в работе [4]. Электрическое поле за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
и наоборот. Эти особенности приводят к дополнительным следствиям, которые впервые были рассмотрены в работе [4]. Электрическое поле за пределами заряженного длинного стержня, на единицу длины которого приходится заряд 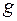 , убывает по закону
, убывает по закону 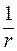 , где
, где 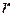 - расстояние от центральной оси стержня до точки наблюдения
- расстояние от центральной оси стержня до точки наблюдения
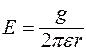 .
.
Если параллельно оси стержня в поле 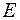 начать двигать со скоростью
начать двигать со скоростью 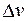 другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле 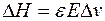 . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью 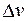 , то уже за счет движения в поле
, то уже за счет движения в поле 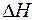 появится добавка к электрическому полю
появится добавка к электрическому полю 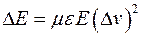 . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля 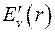 в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости 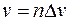 , когда
, когда 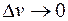 , а
, а 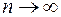 . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением
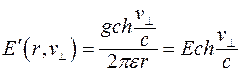 .
.
Если речь идет об электрическом поле одиночного заряда 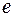 , то его электрическое поле будет определяться соотношением
, то его электрическое поле будет определяться соотношением
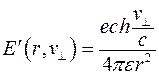 ,
,
где 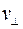 - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения. Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [1-3]:
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения. Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [1-3]:
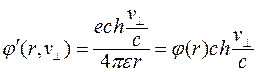 , (4)
, (4)
где 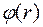 - скалярный потенциал неподвижного заряда. Потенциал
- скалярный потенциал неподвижного заряда. Потенциал 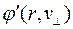 может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Поскольку
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Поскольку 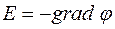 , из соотношения (4) можно вычислить электрические поля движущегося заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
, из соотношения (4) можно вычислить электрические поля движущегося заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
При движении в магнитном поле, применяя уже рассмотренный метод, получаем
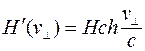 .
.
где 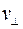 - скорость нормальная к направлению магнитного поля.
- скорость нормальная к направлению магнитного поля.
Если применить полученные результаты к электромагнитной волне и обозначить компоненты полей параллельные скорости ИСО, как 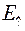 и
и 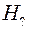 , а
, а 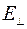 и
и 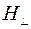 , как компоненты нормальные к ней, то преобразования полей запишутся
, как компоненты нормальные к ней, то преобразования полей запишутся
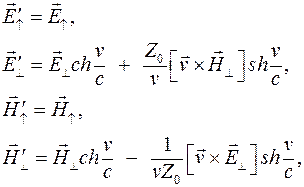 (5)
(5)
где 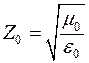 – импеданс свободного пространства,
– импеданс свободного пространства, 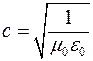 – скорость света.
– скорость света.
Преобразования полей (5) были впервые получены в работе [4].
Литература.
1. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков,
Константа, 2003.- 72 с.
2. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008,
– 153 с. ISBN 978-966-8603-23-5
3. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
4. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
 2015-05-10
2015-05-10 463
463







