1. Вычислить неопределенные интегралы. В пункте а) результаты проверить дифференцированием.
1.1. а) 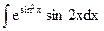 ; б)
; б) 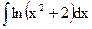 ; в)
; в) 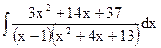 ;
;
1.2. а) 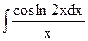 ; б)
; б) 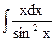 ; в)
; в) 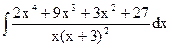 ;
;
1.3. а) 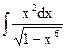 ; б)
; б) 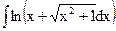 ; в)
; в) 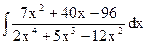 ;
;
1.4. а) 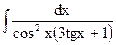 ; б)
; б) 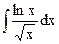 ; в)
; в) 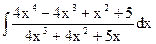 ;
;
1.5. а) 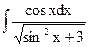 ; б)
; б) 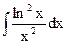 ;в)
;в) 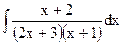 ;
;
1.6. а) 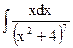 ; б)
; б) 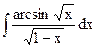 ; в)
; в) 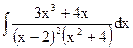 ;
;
1.7. а) 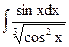 ; б)
; б) 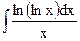 ; в)
; в) 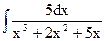 ;
;
1.8. а) 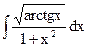 ; б)
; б) 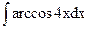 ; в)
; в) 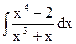 ;
;
1.9. а) 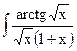 ; б)
; б) 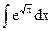 ; в)
; в) 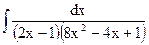 ;
;
1.10. а) 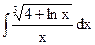 ; б)
; б) 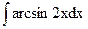 ; в)
; в) 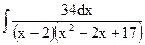 ;
;
1.11. а) 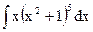 ; б)
; б) 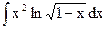 ; в)
; в) 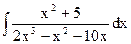 ;
;
1.12. а) 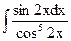 ; б)
; б) 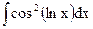 ; в)
; в) 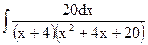 ;
;
1.13. а) 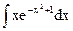 ; б)
; б) 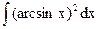 ; в)
; в) 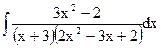 ;
;
1.14. а) 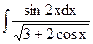 ; б)
; б) 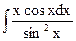 ; в)
; в) 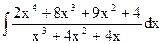 ;
;
1.15. а) 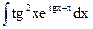 ; б)
; б) 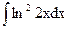 ; в)
; в) 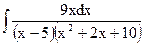 ;
;
1.16. а) 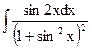 ; б)
; б) 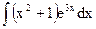 ; в)
; в) 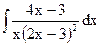 ;
;
1.17. а) 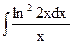 ; б)
; б) 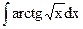 ; в)
; в) 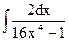 ;
;
1.18. а) 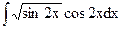 ; б)
; б) 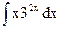 ; в)
; в) 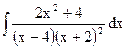 ;
;
1.19. а) 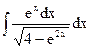 ; б)
; б)  ; в)
; в) 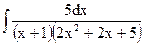 ;
;
1.20. а) 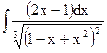 ; б)
; б) 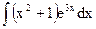 ; в)
; в) 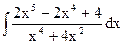 ;
;
1.21. а) 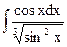 ; б)
; б) 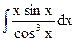 ; в)
; в) 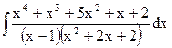 ;
;
1.22. а) 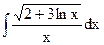 ; б)
; б) 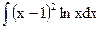 ; в)
; в) 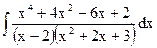 ;
;
1.23. а) 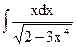 ; б)
; б) 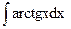 ; в)
; в) 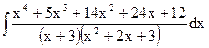 ;
;
1.24. а) 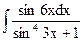 ; б)
; б) 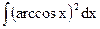 ; в)
; в) 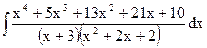 .
.
2. Вычислить определенные интегралы.
2.1. 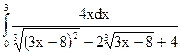 ; 2.2.
; 2.2. 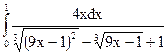 ;
;
2.3. 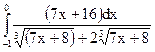 ; 2.4.
; 2.4. 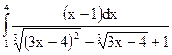 ;
;
2.5. 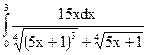 ; 2.6.
; 2.6. 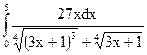 ;
;
2.7. 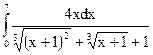 ; 2.8.
; 2.8. 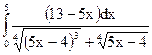 ;
;
2.9. 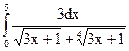 ; 2.10.
; 2.10. 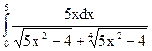 ;
;
2.11. 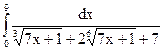 ; 2.12.
; 2.12. 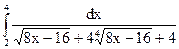 ;
;
2.13. 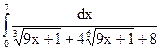 ; 2.14.
; 2.14. 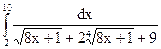 ;
;
2.15. 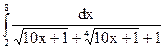 ; 2.16.
; 2.16. 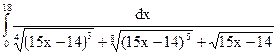 ;
;
2.17. 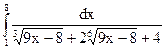 ; 2.18.
; 2.18. 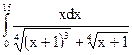 ;
;
2.19.  ; 2.20.
; 2.20. 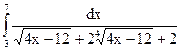 ;
;
2.21. 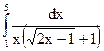 ; 2.22.
; 2.22. 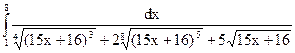 ;
;
2.23. 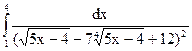 ; 2.24.
; 2.24. 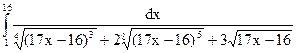 .
.
3.1. 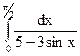 ; 3.2.
; 3.2.  ; 3.3.
; 3.3. 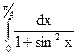 ;
;
3.4. 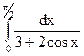 ; 3.5.
; 3.5. 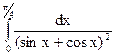 ; 3.6.
; 3.6. 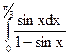 ;
;
3.7. 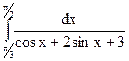 ; 3.8.
; 3.8. 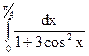 ; 3.9.
; 3.9. 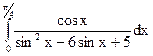 ;
;
3.10. 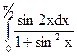 ; 3.11.
; 3.11. 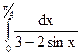 ; 3.12.
; 3.12. 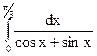 ;
;
3.13. 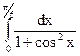 ; 3.14.
; 3.14. 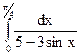 ; 3.15.
; 3.15. 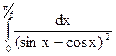 ;
;
3.16. 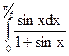 ; 3.17.
; 3.17. 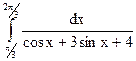 ; 3.18.
; 3.18. 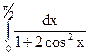 ;
;
3.19. 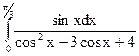 ; 3.20.
; 3.20. 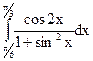 ; 3.21.
; 3.21. 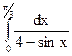 ;
;
3.22. 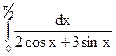 ; 3.23.
; 3.23. 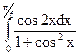 ; 3.24.
; 3.24. 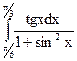 .
.
4. Вычислить несобственные интегралы или установить их расходимость.
4.1. 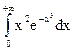 ; 4.2.
; 4.2.  ; 4.3.
; 4.3. 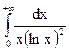 ;
;
4.4.  ; 4.5.
; 4.5. 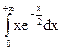 ; 4.6.
; 4.6. 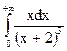 ;
;
4.7. 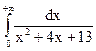 ; 4.8.
; 4.8. 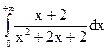 ; 4.9.
; 4.9. 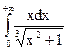 ;
;
4.10. 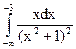 ; 4.11.
; 4.11. 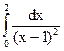 ; 4.12.
; 4.12. 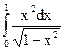 ;
;
4.13.  ; 4.14.
; 4.14. 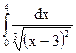 ; 4.15.
; 4.15. 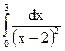 ;
;
4.16. 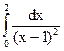 ; 4.17.
; 4.17. 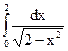 ; 4.18.
; 4.18. 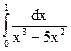 ;
;
4.19. 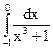 ; 4.20.
; 4.20. 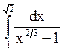 ; 4.21.
; 4.21. 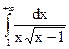 ;
;
4.22. 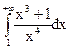 ; 4.23.
; 4.23. 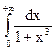 ; 4.24.
; 4.24. 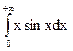 .
.
5.1. Вычислить площадь фигуры, ограниченной параболой 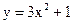 и прямой
и прямой 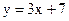 .
.
5.2. Вычислить площадь фигуры, ограниченной графиками функций 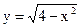 ,
, 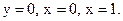
5.3. Вычислить площадь фигуры, ограниченной одной аркой циклоиды 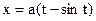 ,
, 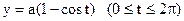 и осью ОХ.
и осью ОХ.
5.4. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями:
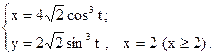
5.5. Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах 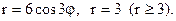
5.6. Вычислить площадь фигуры, ограниченной четырехлепестковой розой 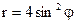 .
.
5.7. Вычислить длину дуги кривой, заданной уравнениями в декартовой системе координат 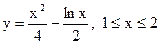 .
.
5.8. Вычислить длину дуги полукубической параболы 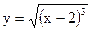 от точки А(2; 0) до точки В(6; 8).
от точки А(2; 0) до точки В(6; 8).
5.9. Вычислить длину дуги кривой, заданной параметрическими уравнениями:
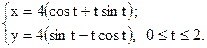
5.10. Вычислить длину одной арки циклоиды 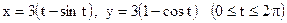 .
.
5.11. Вычислить длину дуги кривой, заданной уравнениями в полярных координатах
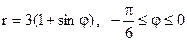 .
.
5.12. Вычислить длину кардиоиды 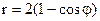 .
.
5.13. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной кривыми 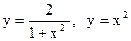 .
.
5.14. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами 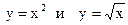 .
.
5.15. Вычислить объем тела, ограниченного поверхностями 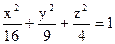 ;
;
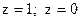 .
.
5.16. Найти площадь фигуры, ограниченной кардиоидой 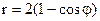 и окружностью
и окружностью 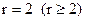 .
.
5.17. Найти площадь фигуры, ограниченной полукубической параболой 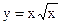 , прямой у=8 и осью ОУ.
, прямой у=8 и осью ОУ.
5.18. Найти площадь фигуры, ограниченной кривой 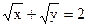 и осями координат.
и осями координат.
5.19. Найти площадь фигуры, ограниченной окружностями 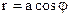 и
и 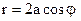
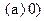 .
.
5.20. Вычислить длину дуги кривой 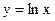 от
от 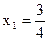 до
до 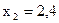 .
.
5.21. Найти площадь фигуры, ограниченной параболой 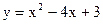 и прямой
и прямой 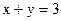 .
.
5.22. Найти площадь фигуры, ограниченной кардиоидой 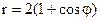 и окружностью
и окружностью 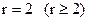 .
.
5.23. Найти длину одной арки циклоиды 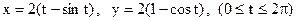 .
.
5.24. Найти объем тела, ограниченного поверхностями 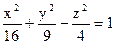 ,
, 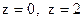 .
.
Литература:
Основная:
1. В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов. Краткий курс высшей математики. Т. 1., Т. 2. – М.: Высшая школа, 1978.
Дополнительная:
1. О.В. Мантуров, Н.М. Матвеев. Курс высшей математики. – М.: Высшая школа, 18986, ч. 1,2.
2. О.В. Зимина Линейная алгебра и аналитическая геометрия: Учебное пособие для студентов вузов. – М.: Издательство МЭИ, 2000.
3. В.С. Шипачев. Высшая математика: Учебник для вузов. – 5-е издание. – М.: Высшая школа, 2002.
 2015-05-13
2015-05-13 366
366







