Каноническая форма задачи

Основной метод решения задачи ЛП - симплекс-метод обычно применяется к ограничениям в виде равенства, т. е. Ax = b, x ≥ 0. Такая форма задачи называется канонической. Для ее построения неравенства исходной задачи преобразовываются в равенства с помощью искусственных переменных, которые также являются неотрицательными. В результате этого действия происходит расширение области решений исходной задачи, другими словами, она становится подмножеством области решения новой – канонической задачи.

Следует отметить, что область решений канонической задачи сохраняет основные геометрические

свойства области исходной задачи, т. е. содержит ее в виде своего подмножества.

Пусть, например, исходная задача имеет вид

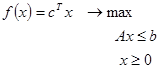
Для того чтобы преобразовать ограничения – неравенства этой задачи, добавим в каждое из m неравенств системы Ax £ b по одной искусственной переменной у_i, i = 1,…, m, превратив тем самым неравенства 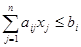в равенства 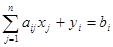, i = 1,…, m. Тогда новая форма задачи (расширенная, каноническая) будет иметь вид

,

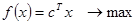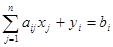, i = 1,…, m,

х_j ³ 0 "j; y_i ³ 0 " i

или в матричной форме

,

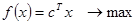Ax + Iy = b

х, y ≥ 0

где I – единичная матрица размерности (mхm). В принципе, в новой задаче можно выполнить обозначение переменных, например, х_{п+ i} = y_i, i = 1, …, m, и представить расширенную задачу в форме

,

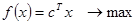Ax = b

х ≥ 0

где вектор х содержит как старые, так и новые переменные, т. е. имеет размерность (m+n)x1, в матрице А уже появились новые столбцы, соответствующие столбцам единичной матрицы I, а последние m координат вектора с равны нулю, так как искусственные переменные отсутствуют в целевой функции. Сохраняя для числа переменных прежнее обозначение п + m: = п, можно вновь считать, что расширенная задача (т.е. каноническая форма) имеет п переменных и m ограничений, другими словами, считать матрицу А размерности (mхп), причем, m < п.

Иллюстрирует построение канонической формы задачи на примере

f(x) = 2x₁ + 3x₂ + 5x₃ → max.

x₁ + x₂ - 5x₃ ≥ -5

-6x₁ + 7x₂ - 9x₃ ≤ 4

x₁ + x₂ + 4x₃ = 10

x₁, x₂, x₃ ≥ 0

Два из трех ограничений этой задачи являются неравенствами. Преобразуем их в равенства с помощью неотрицательных искусственных переменных х₄ ≥ 0 и х₅ ≥ 0. Первое ограничение примет вид x₁ + x₂ - 5x₃ - х₄ = -5, а второе – вид -6x₁ + 7x₂ - 9x₃ + х₅ = 4. В канонической форме новая задача есть

f(x) = 2x₁ + 3x₂ + 5x₃ → max.

x₁ + x₂ - 5x₃ - х₄ = -5

-6x₁ + 7x₂ - 9x₃ + х₅ = 4

x₁ + x₂ + 4x₃ = 10

x₁, x₂, x_3, х₄, х₅ ≥ 0

Теперь целевую функцию можно записать в виде 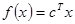, где с = (2, 3, 5, 0, 0)^Т, х = (х₁, …, х₅)^Т, а ограничения имеют вид Ах = b, где матрица А имеет размерность (3х5), последние два столбца которой соответствуют переменным х₄ и х₅.