Следующий член в разложении (6.38) приводит к векторному потенциалу
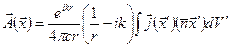 . (6.53)
. (6.53)
Это выражение можно представить в виде суммы двух членов, один из которых дает поперечное магнитное поле, а другой – поперечное электрическое. Эти физически различные компоненты можно разделить, записывая подынтегральное выражение в (6.53) в виде суммы симметричной и антисимметричной частей:
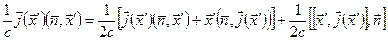 . (6.54)
. (6.54)
Вторая антисимметричная часть, очевидно, связана с намагниченностью, обусловленной током:
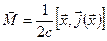 . (6.55)
. (6.55)
Первый, симметричный член, как будет показано ниже, связан с электрическим квадрупольным моментом.
Рассматривая только магнитный член, получаем
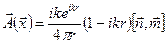 , (6.56)
, (6.56)
где 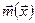 - магнитный дипольный момент
- магнитный дипольный момент
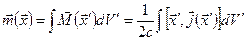 . (6.57)
. (6.57)
Переходя к вычислению полей, заметим, что векторный потенциал (6.56) с точностью до множителя равен магнитному полю (6.44) электрического диполя, если 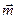 заменить на
заменить на 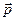 . Поэтому магнитное поле диполя будет равно электрическому полю электрического диполя с заменой
. Поэтому магнитное поле диполя будет равно электрическому полю электрического диполя с заменой 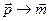 . Таким образом, получаем
. Таким образом, получаем
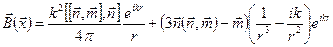 . (6.58)
. (6.58)
Теперь легко установить, что электрическое поле имеет вид
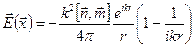 , (6.59)
, (6.59)
т.е. равно взятому с обратным знаком магнитному полю электрического диполя. Все выводы, относящиеся к поведению полей в ближней и дальней зонах, остаются теми же, что и для электрического дипольного источника, если только сделать замену 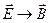 ,
, 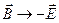 ,
, 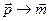 . Аналогично распределение излучения и излучаемая мощность для обоих диполей одинаковы. Единственное различие полей излучения связано с их поляризацией. Для электрического диполя электрический вектор лежит в плоскости, образованной векторами
. Аналогично распределение излучения и излучаемая мощность для обоих диполей одинаковы. Единственное различие полей излучения связано с их поляризацией. Для электрического диполя электрический вектор лежит в плоскости, образованной векторами 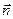 и
и 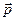 , в то время как для магнитного диполя он перпендикулярен плоскости, проходящей через
, в то время как для магнитного диполя он перпендикулярен плоскости, проходящей через 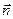 и
и 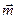 .
.
Интеграл от симметричного члена в (6.54) после интегрирования по частям и некоторых преобразований приводится к виду
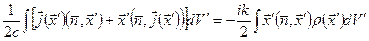 . (6.60)
. (6.60)
Здесь 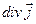 заменена на
заменена на 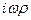 согласно уравнению непрерывности. Так как этот интеграл содержит второй момент плотности заряда, то, следовательно, он соответствует электрическому квадрупольному источнику. Векторный потенциал имеет вид
согласно уравнению непрерывности. Так как этот интеграл содержит второй момент плотности заряда, то, следовательно, он соответствует электрическому квадрупольному источнику. Векторный потенциал имеет вид
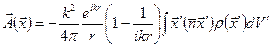 . (6.61)
. (6.61)
Выражения для полей в общем случае довольно сложны, и мы ограничимся рассмотрением полей в волновой зоне. Тогда легко видеть, что
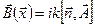 ,
, 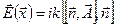 , (6.62)
, (6.62)
Таким образом, для магнитного поля получаем
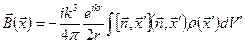 . (6.63)
. (6.63)
Используя определение тензора квадрупольного момента
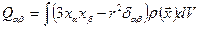 , (6.64)
, (6.64)
можно записать интеграл (6.63) в виде
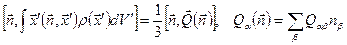 . (6.65)
. (6.65)
Заметим, что величина и направление вектора 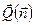 зависят как от направления наблюдения, так и от свойств источника.
зависят как от направления наблюдения, так и от свойств источника.
В этих обозначениях магнитное поле запишется в виде
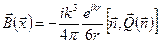 , (6.66)
, (6.66)
а средняя мощность, излучаемая в единичный телесный угол – в виде
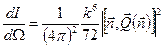 . (6.67)
. (6.67)
Угловое распределение имеет довольно сложный характер. Однако мощность излучения вычисляется непосредственно. Учитывая определение 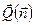 , представим угловую зависимость в виде
, представим угловую зависимость в виде
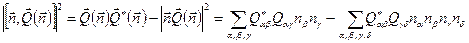 . (6.68)
. (6.68)
Вычисление угловых интегралов от произведений прямоугольных составляющих 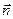 дает
дает
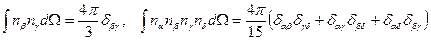 . (6.69)
. (6.69)
Откуда
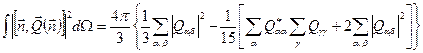 . (6.70)
. (6.70)
Так как сумма элементов тензора 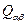 , стоящих на главной диагонали, равна нулю, первый член в квадратных скобках тождественно обращается в нуль. Отсюда получается окончательное выражение для полной мощности излучения квадрупольного источника
, стоящих на главной диагонали, равна нулю, первый член в квадратных скобках тождественно обращается в нуль. Отсюда получается окончательное выражение для полной мощности излучения квадрупольного источника
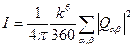 . (6.71)
. (6.71)
При заданном квадрупольном моменте излучаемая мощность пропорциональна шестой степени частоты в отличие от дипольного излучения, где она пропорциональна четвертой степени частоты.
Во временной области можно получить следующие выражения для магнитного поля и интенсивностей магнитно-дипольного и квадрупольного излучений:
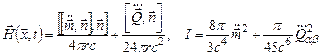 . (6.73)
. (6.73)
Простым примером квадрупольного источника является осциллирующее сфероидальное распределение зарядов. В этом случае недиагональные элементы 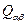 равны нулю, а диагональные элементы можно представить как
равны нулю, а диагональные элементы можно представить как
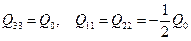 .
.
При этом угловое распределение излучаемой мощности будет иметь вид
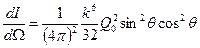 .
.
Соответствующая диаграмма направленности имеет максимумы при 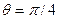 и
и 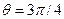 . Полная мощность такого квадруполя равна
. Полная мощность такого квадруполя равна 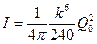 .
.
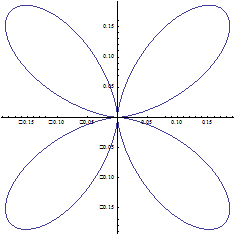 |
| Диаграмма направленности осциллирующего сфероидального распределения зарядов. |
 2015-05-13
2015-05-13 1282
1282








