Эксергия

Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.

Математически второй закон термодинамики может быть выражен следующим образом:

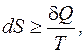(5.1)

где 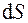– бесконечно малое приращение энтропии системы;

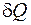– бесконечно малое количество теплоты, полученное системой от источника теплоты.

Знак равенства соответствует обратимым процессам, знак неравенства – необратимым. Чем выше степень необратимости процессов, тем сильнее возрастание энтропии.

Первый и второй законы термодинамики для обратимых процессов могут быть записаны совместно в виде термодинамических тождеств:

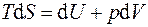; (5.2)

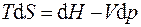. (5.3)

Эксергия системы – это максимальная работа, которую может совершить система при переходе в состояние равновесия с окружающей средой. Эксергетический анализ работы теплоэнергетических и технологических установок учитывает не только количественные, но и качественные характеристики энергоресурсов в различных элементах установок, а также необратимость протекающих в них процессов.

Эксергия тепла термодинамического процесса 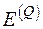, Дж находится как

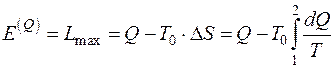, (5.4)

где Q – теплота термодинамического процесса, Дж;

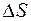– изменение энтропии рабочего тела, Дж/К;

Т ₀ – температура окружающей среды, К.

Эксергия является экстенсивной функцией состояния, поэтому удельная эксергия тепла 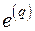, Дж/К определяется как

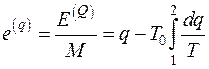. (5.5)

Графически удельная эксергия тепла представлена на рис 5.1. Общая площадь под кривой процесса 1–2 соответствует количеству удельной теплоты процесса q. Она состоит из эксергии тепла процесса (площади, заштрихованной вертикальными линиями) и неработоспособной части тепла 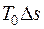(площади, заштрихованной горизонтальными линиями).

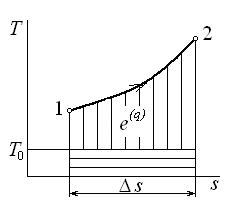
Рис. 5.1. Эксергия тепла термодинамического процесса

Потери работоспособности 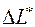(эксергетические потери) за счет необратимости процессов, протекающих в системе, определяются по формуле Гюи-Стодолы

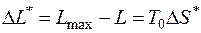, (5.6)

где ­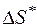– полное приращение энтропии всех подсистем, входящих в данную систему.

Если в исходном состоянии термодинамическая система имеет параметры U, S, V, а в конечном – находится в равновесии с окружающей средой и имеет параметры 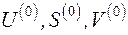, то эксергия неподвижной термодинамической системы E определяется как

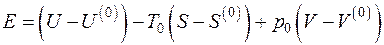, (5.7)

а удельная эксергия e неподвижной системы как

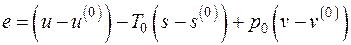, (5.8)

где 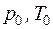– параметры окружающей среды.

Для неподвижной системы, совершающей некоторый обратимый процесс 1–2, максимальная работа равна убыли эксергии:

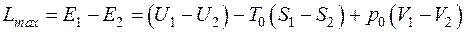. (5.9)

Тогда для необратимого процесса уравнение баланса эксергии примет вид

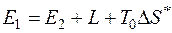, (5.10)

то есть при переходе из состояния 1 в состояние 2 эксергия системы расходуется на совершение работы L, а часть работоспособности теряется из-за необратимости процессов.

При нахождении эксергии потока вещества в форме Лагранжа система координат движется вместе с потоком. Если начальные параметры потока H, S, а конечные соответствуют состоянию равновесия потока с окружающей средой 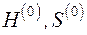, то выражение для эксергии потока в форме Лагранжа 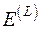имеет вид

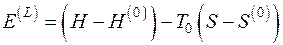, (5.11)

а для удельной эксергии потока :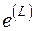

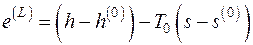. (5.12)

Максимальная внешняя работа совершается за счет убыли эксергии потока

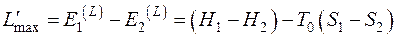. (5.13)

Эксергетические потери находятся также по формуле Гюи-Стодолы

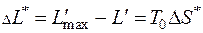, (5.14)

тогда уравнение баланса эксергии потока имеет вид

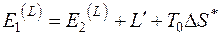. (5.15)

Задачи

5.1. Вычислить эксергию тепла изобарного процесса нагрева воздуха от температуры 20 ^оС до температуры 900 ^оС, если теплоемкость воздуха с_р = 1 кДж/кг, а температура окружающей среды 15 ^оС.