2015-05-13
5534
Начальный удельный объем воздуха находим из уравнения состояния, записанного для 1 кг газа (1.5)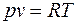 
:
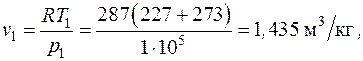
здесь газовая постоянная воздуха находится как
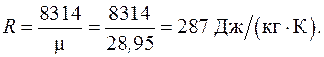
Таблица 6.1
Термодинамические процессы идеального газа
| Величина | Процессы | ||
| Политропный | Адиабатный (изоэнтропный)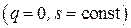
| ||
| Уравнение процесса |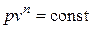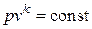 
| 
| |
| Показатель политропы |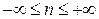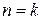
|
| |
| Связь начальных и конечных параметров |  ;  ;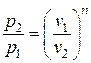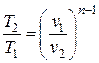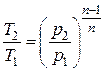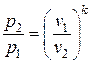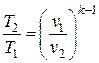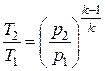
|  ;  ;
| |
| Теплоемкость с |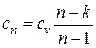 
| ||
| Удельная работа l |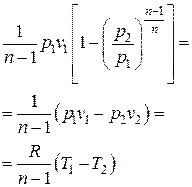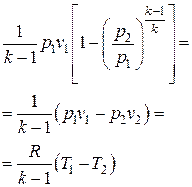 
| 
| |
| Удельная внешняя работа l¢ |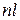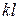
|
| |
| Удельная теплота q |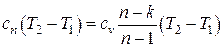 
| ||
| Изменение удельной внутренней энергии D u |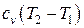
| ||
| Изменение удельной энтальпии D h |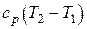
| ||
| Изменение удельной энтропии D s |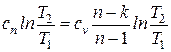
| ||
Таблица 6.2
Термодинамические процессы идеального газа
| Величина | Процессы | ||
Изохорный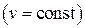 
| Изобарный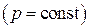
| Изотермический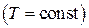
| |
| Уравнение процесса |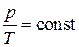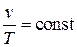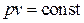 
| 
|
|
| Показатель политропы |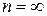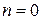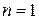
|
|
|
| Связь начальных и конечных параметров |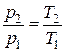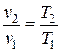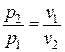
|
|
|
| Теплоемкость с |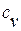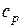
|
| ¥ |
| Удельная работа l |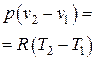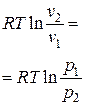
|
| |
| Удельная внешняя работа l¢ |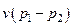
| ||
| Удельная теплота q |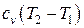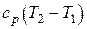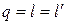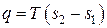
|
| 
|
| Изменение удельной внутренней энергии D u |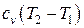
| ||
| Изменение удельной энтальпии D h |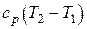
| ||
| Изменение удельной энтропии D s |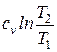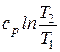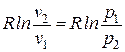 
| 
| 
|
Удельный объем воздуха в конце процесса находится из уравнения политропного процесса в p–v координатах:
|
|
|
;
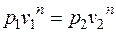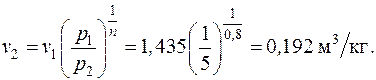
Температура воздуха в конце процесса находится из уравнения политропного процесса в p–T координатах:
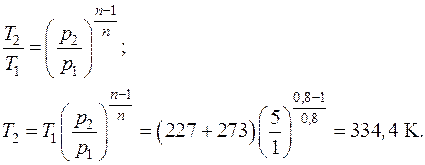
или из уравнения состояния идеального газа (1.5):
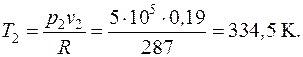
Теплоемкости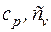 
находятся по молекулярно-кинетической теории с использованием табл. 3.1 (воздух – двухатомный газ):
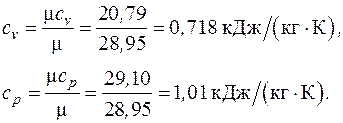
Формулы для расчета удельных количеств теплоты, работы изменения объема и внешней полезной работы, удельного изменения термодинамических функций состояния – внутренней энергии, энтальпии, энтропии берем из табл. 6.1. Показатель адиабаты для двухатомного газа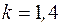 
:
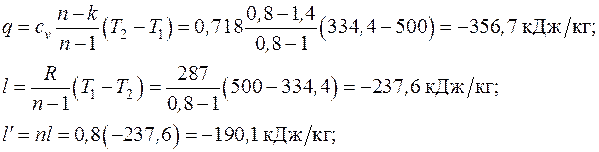
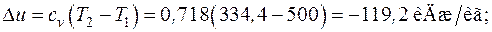
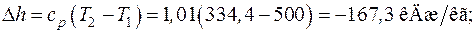
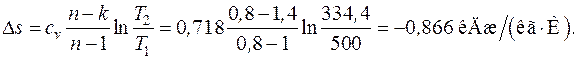Рассчитанный политропный процесс изобразим в диаграммах p–v и T–s (рис. 6.6)
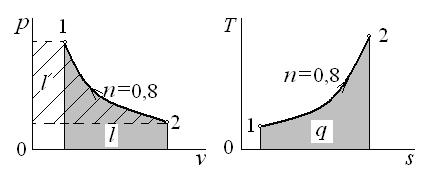
Рис. 6.6. К задаче 5.1
6.2. В закрытом сосуде объемом 0,6 м3 содержится воздух при давлении 5 бар и температуре 20 оС. В результате охлаждения сосуда от воздуха отводится 100 кДж теплоты. Принимая теплоемкость постоянной, определить конечное давление и температуру воздуха.
Ответ: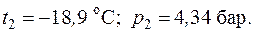 
6.3. 1 кг воздуха сжимается адиабатически так, что его объем уменьшается в 6 раз, а затем в изохорном процессе давление воздуха увеличивается в 1,5 раза. Найти суммарное изменение энтропии газа.
Ответ: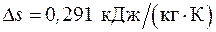 
.
6.4. Воздух с абсолютным давлением 1,2 ат и температурой 60 оС сжимается политропно до абсолютного давления 6 ат. Показатель политропы n = 1,3. Начальный объем воздуха 0,4 м3. Определить конечные объем и температуру воздуха, полные работу и теплоту процесса, а также полное изменение термодинамических функций состояния – внутренней энергии, энтальпии, энтропии.
|
|
|
Ответ:
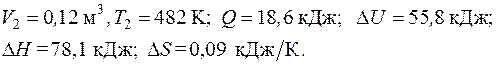
6.5. К 1 кг идеального двухатомного газа подведена теплота, численно равная половине полученной работы. Найти показатель политропы процесса. Изобразить процесс в диаграммах p–v и T–s.
