|
Определение. Пусть у нас заданы группа  и подгруппа и подгруппа  , пусть также дан элемент , пусть также дан элемент  . Левым смежным классом называется множество . Левым смежным классом называется множество  . Правым смежным классом называется множество . Правым смежным классом называется множество  . . Примеры:
1) Пусть 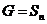 и и 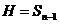 - группы подстановок. Доопределим подстановки из - группы подстановок. Доопределим подстановки из  следующим образом: следующим образом:  они переводят в они переводят в  . Тогда получим, что . Тогда получим, что  - это подгруппа - это подгруппа  . Пусть . Пусть  . Левый смежный класс – это по определению множество . Левый смежный класс – это по определению множество  . Т.к. . Т.к.  имеем, что имеем, что  , то , то  . Верно и обратное, если . Верно и обратное, если  , то , то 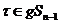 . Т.е. левый смежный класс . Т.е. левый смежный класс  - это множество подстановок, переводящих - это множество подстановок, переводящих  в в  . .
2) Аналогично пусть  и и  и и  . Аналогичными рассуждениями можно получить, что . Аналогичными рассуждениями можно получить, что  - это множество подстановок, переводящих - это множество подстановок, переводящих  в в  . . На этих примерах видно, что левый смежный класс не совпадает с правым, т.е.  . . Предложение.  . .
Доказательство.
Пусть  при при  . .  . Убедимся в том, что все элементы . Убедимся в том, что все элементы  различны. Если различны. Если  , то , то  , следовательно, , следовательно,  , следовательно , следовательно  , следовательно , следовательно  . .
Если  , то аналогичными рассуждениями получаем, что , то аналогичными рассуждениями получаем, что  . .  Предложение. Если 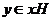 , тогда , тогда 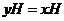 . .
Доказательство.
Т.к.  , то , то 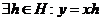 . Тогда . Тогда  имеем, что имеем, что  , следовательно, , следовательно,  . Обратно. Т.к. . Обратно. Т.к.  , то , то  имеем, что имеем, что 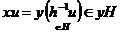 , следовательно , следовательно  , т.е. , т.е.  . .  Следствие. Любые два левых (правых) смежных класса либо совпадают, либо не пересекаются. Теорема (Лагранж). Пусть  - подгруппа конечной группы - подгруппа конечной группы  , тогда , тогда 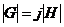 , где , где  - число различных левых (правых) смежных классов - число различных левых (правых) смежных классов 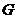 по по  . .
Доказательство.
Пусть  , тогда , тогда  . Т.е. любой элемент группы . Т.е. любой элемент группы 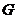 попадает в некоторый смежный класс, таким образом, вся группа попадает в некоторый смежный класс, таким образом, вся группа  разбивается на разбивается на 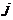 непересекающихся множеств, каждое из которых имеет непересекающихся множеств, каждое из которых имеет  элементов, следовательно элементов, следовательно  . . 
Упражнение. Докажите, что 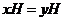 тогда и только тогда, когда тогда и только тогда, когда  . . Следствие 1. Порядок элемента делит порядок группы.
Доказательство.
Пусть  , тогда , тогда 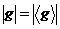 . По теореме Лагранжа . По теореме Лагранжа  делит порядок группы, следовательно и порядок элемента делит порядок группы. делит порядок группы, следовательно и порядок элемента делит порядок группы.  Следствие 2. Группа простого порядка циклическая.
Доказательство.
Пусть 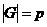 - простое число. Возьмем элемент - простое число. Возьмем элемент 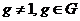 , тогда , тогда  и и  делит делит  . Следовательно . Следовательно  , следовательно , следовательно  и и  . .  Теорема. Пусть  - конечная подгруппа в - конечная подгруппа в  . Тогда . Тогда  - циклическая. - циклическая.
Доказательство.
Пусть  , если , если  , то по следствию 1 , то по следствию 1  , т.е. любой элемент из , т.е. любой элемент из  является корнем является корнем  -й степени из 1. Следовательно -й степени из 1. Следовательно  . .  циклическая, а подгруппа циклической группы тоже циклическая. циклическая, а подгруппа циклической группы тоже циклическая.  Упражнение. Докажите эту теорему для любого поля.
|

 . Левый смежный класс – это по определению множество
. Левый смежный класс – это по определению множество 








