|
ДИСКРЕТНЫЕ ПОДГРУППЫ В 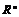
Определение. Аддитивная подгруппа 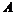 в в 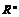 называется дискретной, если существует окрестность нуля называется дискретной, если существует окрестность нуля 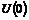 , такая что , такая что 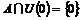 , т.е. в некоторой окрестности нуля нет ни одного элемента подгруппы , т.е. в некоторой окрестности нуля нет ни одного элемента подгруппы 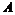 кроме нулевого. кроме нулевого.
Теорема. Дискретная подгруппа в 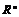 свободна. свободна.
Доказательство.
Пусть 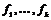 - максимальная независимая (над - максимальная независимая (над 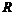 ) система векторов из ) система векторов из 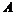 . Если . Если 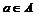 , то , то 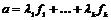 , где , где 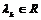 . Разложим . Разложим 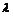 на целые и дробные части: на целые и дробные части: 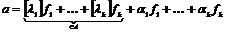 , где , где 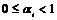 , следовательно, , следовательно, 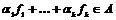 . Рассмотрим множество . Рассмотрим множество 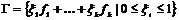 - компакт. - компакт.
Лемма. 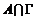 - конечно. - конечно.
Доказательство.
Если 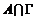 бесконечно, то в бесконечно, то в 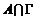 существует сходящаяся последовательность существует сходящаяся последовательность 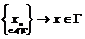 , следовательно , следовательно 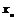 - последовательность Коши, т.е. - последовательность Коши, т.е. 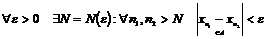 . Следовательно в любой окрестности нуля . Следовательно в любой окрестности нуля 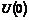 будут элементы из будут элементы из 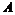 , что противоречит дискретности , что противоречит дискретности 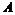 . Следовательно . Следовательно 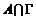 конечно. конечно. 
Таким образом, получили, что 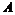 - конечно-порожденная группа (порождается элементами - конечно-порожденная группа (порождается элементами 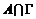 и и  ) и у нее нет элементов конечного порядка. Следовательно она свободна. ) и у нее нет элементов конечного порядка. Следовательно она свободна. 
Теорема. Пусть 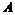 - дискретная подгруппа в - дискретная подгруппа в 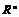 и и 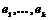 - базис в - базис в 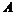 . Тогда . Тогда 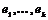 - линейно независимы над - линейно независимы над 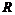 . .
Доказательство.
Пусть эти вектора линейно зависимы, т.е. без ограничения общности можем считать, что 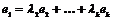 , , 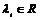 . Рассмотрим множество . Рассмотрим множество 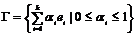 , по лемме , по лемме 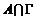 - конечно. Для любого целого - конечно. Для любого целого 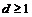 имеем, что имеем, что 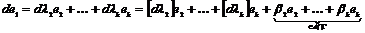 . Этих остатков, принадлежащих . Этих остатков, принадлежащих 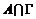 , конечное число, следовательно , конечное число, следовательно 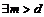 , такое что , такое что 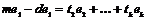 , здесь , здесь 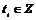 , следовательно , следовательно 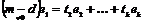 . Следовательно . Следовательно 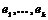 линейно зависимы над линейно зависимы над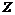 , что невозможно. , что невозможно. 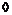
|

