|
Если некоторая часть жидкости приведена в движение и есть сила, поддерживающая это движение, то при небольших скоростях устанавливается слоистое (ламинарное) течение жидкости. На поверхности раздела двух слоев, текущих со скоростями v и 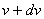 , действуют одинаковые по величине силы f, одна - тормозящая, а другая - ускоряющая движение слоев. Это свойство жидкости называется внутренним трением (вязкостью). , действуют одинаковые по величине силы f, одна - тормозящая, а другая - ускоряющая движение слоев. Это свойство жидкости называется внутренним трением (вязкостью).
Сила взаимодействия слоев
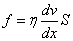 , ,
где, h - коэффициент внутреннего трения,
S - поверхность взаимодействия слоев,
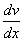 - градиент скорости. - градиент скорости.
На шарик, падающий в исследуемой жидкости, действуют три силы: сила тяжести, подъемная сила и сила сопротивления.
Если шарик медленно падает в безграничной среде, не оставляя за собой завихрений, то, как показал Стокс, сила сопротивления равна:
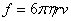 , (1) , (1)
где 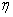 - коэффициент внутреннего трения, - коэффициент внутреннего трения,
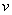 - скорость шарика, - скорость шарика,
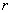 - его радиус. - его радиус.
Вывод этой формулы довольно сложен, его можно найти в специальной литературе. Вид же соотношения, определяющего силу 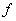 , можно установить с точностью до постоянного множителя, исходя из соображений размерности. , можно установить с точностью до постоянного множителя, исходя из соображений размерности.
Опыт показывает, что сила сопротивления будет тем больше, чем больше коэффициент внутреннего трения 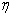 , радиус , радиус 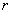 и скорость и скорость 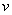 падающего шарика. Таким образом, можно написать: падающего шарика. Таким образом, можно написать:
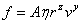 , (2) , (2)
но
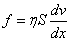 . (3) . (3)
Сравнивая соотношения (2) и (3), нетрудно видеть, что 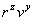 должно иметь размерность должно иметь размерность 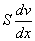 . Так как . Так как
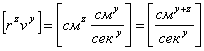 , ,
а
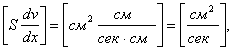
откуда
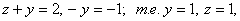
следовательно,
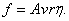
Множитель А этим методом не может быть определен; он получается равным 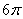 , если решить задачу гидродинамики вязкой жидкости. , если решить задачу гидродинамики вязкой жидкости.
В случае падения шарика в жидкости уравнение движения имеет вид:
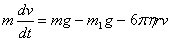 . (4) . (4)
Так как сила сопротивления с увеличением скорости движения шарика возрастает, то наступает момент, когда шарик начинает двигаться равномерно со скоростью  . .
Тогда
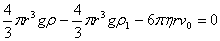 , (5) , (5)
где 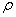 -плотность шарика, -плотность шарика,
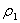 -плотность жидкости, -плотность жидкости,
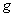 -ускорение силы тяжести. -ускорение силы тяжести.
Из уравнения (5), если d - диаметр шарика, получим:
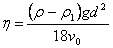 . .
Пусть шарик падает вдоль оси бесконечно длинного цилиндрического сосуда с диаметром D. Учет наличия стенок приводит к следующему выражению:
 . (6) . (6)
Используя выражение (6), определяют коэффициент внутреннего трения по методу Стокса.
Описание установки
Цилиндрический стеклянный сосуд (1), заполненный водой и выполняющий роль термостата, закреплен на штативе (2). В термостате, температура которого измеряется термометром (3), помещен второй круглодонный стеклянный цилиндр (4), заполненный исследуемой жидкостью. На цилиндр нанесен ряд горизонтальных меток. На верхний край цилиндра (4) одет фланец, с помощью которого он опирается на крышку (5) термостата (1).Цилиндр (4) прикрыт в свою очередь пробкой (6),
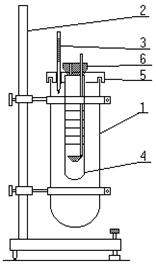
в которой имеется отверстие для ввода шариков в испытуемую жидкость. Для измерения коэффициента внутреннего трения используют шарики, диаметры которых предварительно измеряют с помощью отсчетного микроскопа.
Выполнение работы
1. Определяют цену деления отсчетного микроскопа.
2. Измеряют диаметр шарика (шарик кладут на предметное стекло и вместе с ним помещают на столик микроскопа).
3. Опускают шарик в цилиндр с исследуемой жидкостью, измеряют секундомером время 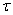 движения шарика между метками. При отсчете глаз надо помещать так, чтобы избежать ошибки из-за параллакса. движения шарика между метками. При отсчете глаз надо помещать так, чтобы избежать ошибки из-за параллакса.
4. Измерив расстояние между метками, определяют скорость движения шарика. Опыт повторяют для разных шариков 10-12 раз.
5. Вычисляют по формуле (6) h для каждого шарика и находят его среднее значение.
Результаты измерений записывают в таблицу:
№опыта |
d(см)
|
l(см)
|
t(сек)
|
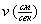
|
h(пуаз)
|
|
|
|
|
|
|
Примечание. Так как вязкость жидкости зависит от температуры, то при измерениях замечают температуру.
|

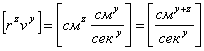 ,
,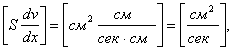
 . (6)
. (6)









