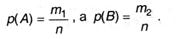А.2. Сложение и умножение вероятностей

Сложение вероятностей независимых, несовместных событий

Пусть среди возможных равновероятных исходов благоприятными оказывается любое из событий А или B, причем А и В - независимы (т.е. между ними отсутствуют причинно-следственные связи - А не влияет на B и наоборот) и несовместны (т.е. они не могут наступить одновременно, а наступает лишь одно из них). Путь из общего числа равновероятных исходов п событие А осуществляется т₁ числом способов, а событие В - т₂. Тогда

Спрашивается, как найти вероятность события С = (А или В)*? С называют также суммой событий A и В. Очевидно, общее число способов, которым может реализоваться С равно m₁ + т₂. Следовательно,

*Используя формализм математической логики, можно записать С = A v B.

Пример 5.1

Способы представления алгоритмов

Постановка задачи кодирования, Первая теорема Шеннона

Пример 9.2.

Пример 3.2.

Вернуться в оглавление: Теоретические основы информатики