Явление стохастического резонанса в нелинейных системах

Понятие «стохастический процесс» относится к области хаоса, к беспорядочному поведению, к процессу, динамика которого случайна и непредсказуема. Известным примером такого процесса является броуновское движение.

Слово "резонанс" в самом общем смысле означает сильный отклик какой-либо системы на небольшое внешнее воздействие. Важно то, что такой сильный отклик - избирателен, то есть он возникает только при определенных параметрах внешнего воздействия. Резонанс возникает, если частота внешнего воздействия сравнивается с собственной частотой колебаний системы.

Вместе же эти два слова означают очень интересное и, на первый взгляд, противоречащее здравому смыслу явление, которое имеет место во многих, совершенно различных системах и даже, как оказывается, уже давно используется природой.

Данное явление было открыто в 80-х годах. Суть стохастического резонанса заключается в том, что добавление в систему шума, т.е. хаотического движения, не уменьшает, а наоборот усиливает отклик системы на слабое периодическое воздействие. При этом шум не только не подавляет сигнал, а, наоборот, помогает ему проявиться. Наиболее сильный эффект возникает при некоторой вполне определенной, оптимальной интенсивности шума.

Любому, кто сталкивался с проблемой выделения полезного сигнала из шума, кажется очевидным утверждение, что первым шагом в этом процессе является максимально возможное уменьшение интенсивности шума. Еще с тех времен на заре радиотехники, когда инженеры впервые услышали раздающееся из динамиков шипение, они ищут способы подавления шумов, неизбежно возникающих в электрических цепях и коммуникационных системах. Считается, что генерировать шум необходимо лишь в ситуациях, когда требуется не дать кому-то надежно принять полезный сигнал.

Идея использовать шум для улучшения качества сигнала кажется абсурдной, ведь ни одному нормальному человеку не придет в голову, например, царапать компакт-диск, чтобы с него стала лучше считываться информация. Однако исследования последних лет позволяют сделать вывод, что в определенных случаях шум может играть конструктивную роль при восприятии слабых сигналов благодаря эффекту, получившему название "стохастический резонанс". Явление оказалось столь необычным, что первое время после открытия оно привлекало внимание очень ограниченного круга ученых, в основном тех, кто его и обнаружил.

Термин «стохастический резонанс» был введен в 1981 году в статье R.Benzi, A.Sutera, A.Vulpiani, J. Phys. A14 L453 (1981), в которой авторы исследовали периодичность наступления ледниковых периодов и обнаружили усиление слабого сигнала при наложении шума. В 1983 году это явление было подробно исследовано в триггере Шмитта и потом было открыто во многих физических, химических и биологических системах.

Стохастический резонанс – это усиление периодического сигнала под действием белого шума определенной мощности. Является универсальным явлением, присущим многим нелинейным системам, находящимся под внешним воздействием одновременно хаотического и слабого периодического воздействия.

Для объяснения данного явления рассмотрим какую-либо бистабильную систему, обладающую диссипацией, трением. Под действием достаточного внешнего воздействия такая система может перейти в другое состояние. Если достаточное внешнее воздействие периодическое, то система, так же, будет периодически переходить из одного состояния в другое. Недостаточное (подпороговое) воздействие не вызовет отклика такой системы. Если внешнее воздействие беспорядочно (шум), то система хаотически «блуждает», и спустя неопределённое время, средняя длина которого зависит от мощности шума, может перескочить из одного положения в другое. Динамика таких скачков будет беспорядочной.

Рассмотрим теперь суммарный эффект подпорогового периодического и хаотического воздействий. Само по себе подпороговое периодическое возмущение не сможет перебросить систему в другое состояние, однако шум помогает этому, подводя воздействие к «критическому» состоянию. В результате в отклике системы проявляется периодичность, определяемая слабым периодическим воздействием.

Оптимальной (приводящей к максимальному отношению сигнала к шуму) является такая мощность шума, при которой характерное время жизни системы в одном состоянии равно половине периода периодического возмущения. Слишком сильный или слишком слабый шум приводят к меньшей чувствительности системы к слабому периодическому воздействию.

Условием для возникновения стохастического резонанса - система должна быть нелинейной, иначе отклик системы на суммарное воздействие будет просто суммой откликов и не приведет ни к каким новым эффектам.

Система должна обладать, по крайней мере, двумя стабильными или метастабильными состояниями. Это может быть как бистабильная система, так и система с долгоживущим метастабильным возбужденным состоянием.

К системам, демонстрирующим стохастический резонанс, относятся, например: динамика ледниковых периодов на Земле; динамика североатлантического климата; накачка в кольцевом лазере; органы чувств у ряда животных.

Рассмотрим для примера какую-либо бистабильную систему. Слова "бистабильная система" - это система с двумя положениями устойчивого равновесия. Простой механический пример - это движение материальной точки в потенциале с двумя минимумами (см. рис.1а). Если на частицу действует еще и сила трения, то ясно, что какие бы мы ни выбрали начальные условия, колебания, в конце концов, затухнут, частица "свалится" в одну из потенциальных ям и будет находиться там неограниченно долго.

Рис. 14.6 Пример поведения бистабильной системы при внешнем на нее воздействии.

Для того, чтобы частица все-таки попала в другую потенциальную яму, надо приложить внешнюю силу. Если эта сила достаточно велика, то она "вытащит" частицу из первой ямы и перекинет ее во вторую. На языке потенциала (в данном тексте потенциал используется как синоним потенциальной энергии) "приложить внешнюю силу" означает добавить линейно растущий потенциал, как это показано на рис. 14б. Если V(x) - бистабильный потенциал, то внешняя сила должна превосходить величину = |V'(x)|, взятой в точке перегиба, т.е. там, где возвращающая сила, создаваемая потенциалом, самая большая. Тогда суммарный потенциал модифицируется так, как показано на рисунке, и частица скатится во вторую яму. Если внешняя сила будет периодична по времени, то в результате частица будет "скакать" из одной ямы в другую и обратно. В результате бистабильная система будет откликаться на сильное внешнее воздействие. При этом частота, с которой система перескакивает из одного устойчивого состояния в другое, совпадает с частотой внешнего воздействия. Если внешнее воздействие очень сильное, то система будет послушно повторять все изменения и колебания этой силы. Если внешнее воздействие окажется не столь сильным, т.е. < , то частица не сможет покинуть яму и останется в ней, несмотря на внешнее воздействие.

Таким образом, бистабильная система может обладать неким порогом чувствительности: при внешней силе > система начинает перескакивать из одного состояния в другое с частотой внешней силы, а при < система не чувствует внешнее воздействие. То есть, у бистабильной системы существует некий порог чувствительности к внешним воздействиям. Слишком слабые, т.е. подпороговые воздействия остаются для системы незамеченными, но при дополнительном воздействии на такую систему, даже стохастическим сигналом может происходить усиление сверхслабых сигналов.

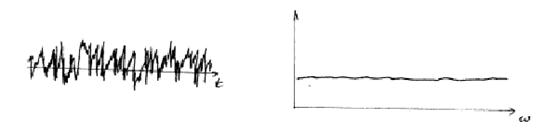
а) б)

Рис. 14.7 Сигналы а) и их Фурье-образы б).

Стохастический сигнал имеет природу случайного шума. С помощью преобразования Фурье можно отделить периодический сигнал от шума.
В рассматриваемой бистабильной системе под действием случайной силой будут происходить случайные колебания. При этом может оказаться так, что частица, блуждая по одной потенциальной яме, вдруг перескочит и во вторую. Очевидно, что чем сильнее шум, тем меньше время перескока, т.е. тем чаще частица перескакивает из одной ямы в другую. Если изобразить зависимость координаты частицы от времени, то получится приблизительно такая картина, как на рис. 14.8.

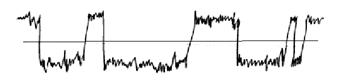
Рис. 14.8 Отклик системы на случайное внешнее воздействие.

Если к внешнему шуму добавить и слабый, подпороговый периодический сигнал, то частица будет по-прежнему скакать из одной ямы в другую, но характер этого процесса изменится: в нем появится периодическая компонента с периодом, равным периоду внешнего слабого сигнала. То есть, перескоки осуществляются за счет случайной силы, а периодическая добавка лишь "модулирует" эффект (т.е. добавляет свою собственную периодичность).

Шум как бы устраняет непреодолимый ранее потенциальный барьер и заставляет систему откликаться на подпороговый сигнал.

В этом заключается суть стохастического резонанса (усиления). Особенность стохастического резонанса заключается в том, что существует некая оптимальная интенсивность шума, при которой отклик системы на периодический сигнал самый сильный. Для того, чтобы определить, насколько велик этот отклик, нужно построить зависимость координаты частицы от времени и с помощью преобразования Фурье выделить периодическую составляющую сигнала. Тогда амплитуда дополнительного "горба" фурье-образа (рис. 14.7) будет служить количественной характеристикой чувствительности системы. Чем выше горб, тем сильнее проявляется внешний периодический сигнал в движении частицы.

t(c)

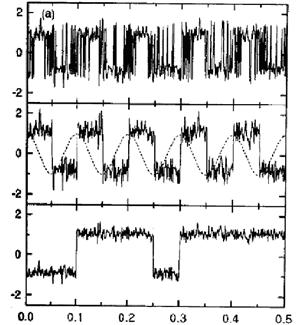
Рис. 14.9 Отклик бистабильной системы при различной интенсивности шума.

На рисунке показана зависимость координаты частицы от времени при одном и том же слабом периодическом сигнале, но при разных интенсивностях шума. Видно, что когда интенсивность шума мала, частица долго находится в одной потенциальной яме, прежде чем перепрыгнуть в другую (рис. 14.9, нижний график). Внешний периодический сигнал здесь никак не проявляется. Когда увеличивается интенсивность шума до оптимальной, частица под суммарным воздействием шума и периодической силы будет синхронно прыгать из одной ямы в другую (рис. 14.9, средний график). Явно видна периодическая составляющая отклика системы, период которой совпадает с периодом внешней силы. Наконец, при дальнейшем усилении шума движение частицы станет все более и более хаотичным; периодическая компонента в отклике будет уменьшаться (рис. 14.9, верхний график).

Типичная зависимость отклика системы от интенсивности внешнего шума показана на рис. 14.10. Видно, что при некоторой интенсивности шума отклик системы на полезный сигнал будет максимальным.

Рис. 14.10 Зависимость от интенсивности шума амплитуд сигналов периодической составляющей.

Определенной интенсивности шума отвечает вполне конкретное среднее время перескока из одной ямы в другую. Условие для оптимальной интенсивности шума: нужно чтобы вызываемое этим шумом время перескока равнялось половине периода слабого периодического возмущения. Когда период перескока и период внешней силы синхронизированы, возникает наиболее сильный отклик системы на внешнее периодическое возмущение (резонанс). Если эти два процесса не синхронизированы, чувствительность к слабой периодической силе уменьшается.

Стохастический резонанс используется в технике, наблюдается и в функционировании живых организмов. Например, стохастический резонанс применяется в оптических системах и возникает при генерации нервных импульсов.

Примером оптической системы, в которой наблюдался стохастический резонанс, служит так называемый кольцевой лазер (рис. ), в котором лазерный свет накачивается в резонаторе с тремя или более зеркалами. В этой системе существует два стабильных режима накачки лазерного света, когда свет движется по направлению движения часовой стрелки или против. Это был один из первых экспериментов (1988 год), когда стохастический резонанс наблюдался в лаборатории.

В начале 90-х годов было осознано, что стохастический резонанс может играть ключевую роль в нейрофизиологических процессах, а именно, в функционировании нейронных сетей, в передаче импульсов от одной группы нейронов другой.

Например, в экспериментах 1991-1993 годов было выяснено, что возникновение нервного импульса в механорецепторных клетках речного рака как раз основано на явлении стохастического резонанса. Благодаря этому, рак может усиками улавливать слабое синхронное колебание воды вокруг себя, несмотря на присутствие разного рода "шумов", и таким образом заранее узнавать о приближении опасности. После этих классических экспериментов хлынул целый поток работ, посвященных роли стохастического резонанса в возникновении и распространении нервных импульсов. Сейчас это уже широко принятая парадигма в биологических и нейрофизиологических науках.

Совсем недавно, во второй половине 90-х годов, возник вопрос о возможности существования стохастического резонанса на квантовом уровне. Ожидается, что квантовое "дрожание частиц", которое существует всегда, даже при абсолютном нуле температуры, и которое играет здесь роль шума, будет способствовать детектированию квантового сигнала, распространению информации и т.д.

Стохастический резонанс может возникать и в системах, отличных от бистабильных. Главное требование - это наличие какого-либо порога. Примером такой системы может служить система, в которой перескоки происходят не между двумя устойчивыми положениями равновесия, а между "основным" и "возбужденным" состояниями системы.

Недавно было описано явление, названное "двойным стохастическим резонансом". Здесь на свободную частицу действуют сразу два типа шумов: первый создает нечто наподобие бистабильного потенциала, а второй заставляет частицу в этом псевдопотенциале скакать. Явление очень интересное, поскольку оно служит прекрасной иллюстрацией того, что шум может не только разрушать тонкие, скоррелированные процессы, но и наоборот - давать им жизнь.

Интересно, что уже в ближайшем будущем, когда сверхминиатюрная электроника выйдет из научных лабораторий и станет доступной массовому пользователю, стохастический резонанс может оказаться важной ее частью.

Например, в 2003 году было обнаружено это явление в самых перспективных «кирпичиках» наноэлектроники будущего — в углеродных нанотрубках (длинных цилиндрических каркасных молекулах, целиком состоящих из углерода). Транзисторы, выполненные на одной нанотрубке, оказались способны регистрировать более слабые зашумленные сигналы, чем ожидалось.

Другой пример дают нейронные сети — электронные устройства, способные эффективно обрабатывать огромные объемы информации. В таких сетях стохастический резонанс будет проявляться в виде улучшенной проводимости зашумленной информации и синхронизации процессов, одновременно происходящих в разных частях сети.

В самые последние годы появился ряд сообщений об успешном использовании стохастического резонанса при обработке сигналов и компьютерном распознавании изображений.

Введение

Физические основы СКВИД - микроскопии

Эффект Джозефсона

Метод Лауэ

Понятия экситона, поляритона, плазмона

Вернуться в оглавление: Современные фундаментальные и прикладные исследования в приборостроении