Понятия классических и квантовых систем

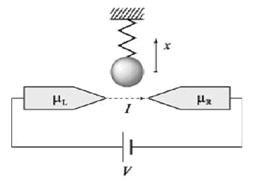
Без понятия "колебаний" немыслима современная физика, а исторически первым хорошо исследованным видом колебаний были механические колебания. Простейшим и занимающим особое место видом колебаний являются колебания гармонические, и потому гармонический осциллятор занимает своё важное место на страницах учебников. Так было до создания квантовой механики, не изменилась ситуация и с её созданием. Однако в квантовой механике, в отличие от "классики", для гармонического осциллятора энергетический спектр уже не является непрерывным, а представляет собой набор дискретных уровней, отделённых друг от друга равными энергетическими интервалами.

Американские ученые недавно показали, что с помощью электрических измерений (регистрируя вольт-амперные характеристики) можно исследовать процесс декогерентизации для такой удобной квантовой системы как механический осциллятор. В работе теоретиков из Лос Аламоса рассматривается (при нулевой температуре) простая модельная система - механический осциллятор вблизи электрического туннельного перехода (рис. 9.1).

Рис. 9.1 Схематическое изображение квантово-классической колебательной системы.

Условия туннелирования электронов зависят от положения металлического шарика и, таким образом, колебания шарика модулируют ток через туннельный переход. При нулевой температуре осциллятор совершает нулевые колебания; в режиме низких напряжений осциллятор не может перейти в возбужденное состояние под действием электрического тока. Однако при более высоких напряжениях, приложенных к переходу, при туннелировании электронов осциллятор может быть возбужден (что, в свою очередь, приводит к изменению условий туннелирования). При этом наличие дробового шума (флуктуаций электрического тока, связанных с дискретностью заряда) должно приводить к тому, что в процессе электрических измерений происходит декогерентизация и квантовая система (осциллятор) становится эффективно классической. Ситуация аналогична той, что имеет место для квантовой системы, находящейся в термостате при ненулевой температуре, поэтому можно говорить об “эффективной температуре”, которая прямо пропорциональна приложенному напряжению.

Хотя переход от квантового поведения к классическому рассматривается при нулевой температуре, уже сейчас возможно проведение подобных экспериментальных исследований с помощью одноэлектронных устройств, работающих при очень низких температурах (милликельвины).

Квантовый осциллятор имеет только одну собственную степень свободы: его собственная энергия полностью определяется его частотой – согласно формуле Планка. Классический же осциллятор имеет две собственные степени свободы: его энергия зависит не только от частоты, но и от амплитуды колебаний. В отличие от классических осцилляций, квантовые осцилляции не имеют амплитуды. Это свойство можно объяснить при допущении, что квантовые осцилляции являются последовательными скачкообразными сменами всего лишь двух “квантовых положений”. Временная развёртка квантовых осцилляций представляет собой не синусоиду, а меандр, верхние и нижние отрезки которого соответствуют пребыванию квантового осциллятора в том или ином из двух своих квантовых положений, причём размах между ними по оси ординат не имеет физического смысла. Квантовый осциллятор, таким образом, является принципиально негармоническим; строго говоря, он и осциллятором то не является, было бы правильнее называть его квантовым пульсатором.

Квантовые пульсаторы являются элементарными “кирпичиками”, из которых построено вещество. Примером квантового пульсатора может служить, например, электрон. Что пульсирует в электроне – пока неизвестно; но физический смысл у квантовых пульсаций электрона никак не меньше, чем у его комптоновской длины волны, которая точно соответствует частоте этих пульсаций.

Квантовый пульсатор выражает собой идею движения во времени в чистом виде: смены его квантовых положений могут происходить в одной пространственной точке, без какого-то ни было движения в пространстве. Пространственное перемещение частиц вещества выражает собой развитие этой идеи, такое перемещение является движением и во времени, и в пространстве – причём существенно, что изначальное движение квантового пульсатора во времени просто дополняется перемещением этого пульсатора, как целого. Таким образом, обнаруживается важное разграничение между энергией движения квантового пульсатора во времени и энергией его движения в пространстве: первая, т.е. собственная энергия квантового пульсатора, присуща ему всегда, а вторая, т.е. его кинетическая энергия – не всегда.

Принципы построения, структуры и режимы работы осцилляторных систем с регулярной динамикой

Кантилеверные сенсоры на основе высокомолекулярных и биополимерных систем

Устройство и принцип работы биологического нейрона

Проблема создания искусственных нейроноподобных измерительных устройств

Вернуться в оглавление: Современные фундаментальные и прикладные исследования в приборостроении