|
При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:
 , ,

где 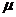 — средняя ошибка выборочной средней; — средняя ошибка выборочной средней;
 — дисперсия выборочной совокупности; — дисперсия выборочной совокупности;
n — численность выборки. При бесповторном отборе она рассчитывается по формуле:
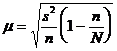 , ,
где N — численность генеральной совокупности. При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:
   , , где 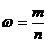 — выборочная доля единиц, обладающих изучаемым признаком; — выборочная доля единиц, обладающих изучаемым признаком;
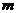 — число единиц, обладающих изучаемым признаком; — число единиц, обладающих изучаемым признаком;
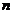 — численность выборки. — численность выборки.
При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:

Предельная ошибка выборки 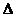 связана со средней ошибкой выборки связана со средней ошибкой выборки 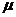 отношением: отношением:
 . .
При этом t как коэффициент доверия (кратности) средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки. Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Метод отбора | Для средней | Для доли | Повторный | 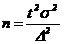
| 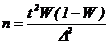
| Бесповторный | 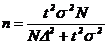
| 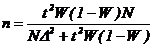
| Значения ? и t определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки, и наоборот (т. е., например, увеличение ошибки выборки в 2 раза уменьшит n в 4 раза).
Вариация ( ) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно ) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно  определяют следующими способами: определяют следующими способами:
1) берут из предыдущих исследований;
2) по правилу «трех сигм» общий размах вариации укладывается в 6 сигм (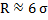 , отсюда , отсюда 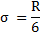 ). Для большей точности R делят на 5; ). Для большей точности R делят на 5;
3) если хотя бы приблизительно известна средняя величина изучаемого признака, то 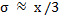 ; ;
4) при изучении альтернативного признака, если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, берется максимально возможная величина дисперсии, равная 0,25.
| 
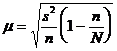 ,
,









