Решение системы нелинейных уравнений

Решение системы нелинейных уравнений производится методом Ньютона – Рафсона, использующий метод последовательных приближений. Метод Ньютона – Рафсона вытекает из представления произвольной функции ¦(х) с помощью ряда Тейлора. В простейшем случае для функции с одной переменной

¦(х) = ¦(хо) + ¦¢(хо) (х-хо) + 0 (х – хо)

Если система состоит из одного нелинейного уравнения ¦(х) = 0, то ¦(X) = ¦(Xо) + ¦¢(Xо) (X-Xо)» 0 и

¦(Xо)

X - Xо = ¦¢(Xо), отсюда

¦(Xо)

X = Xо - ¦¢(Xо)

Для напряжений в дискретной форме это соотношение можно записать в следующем виде

¦(Un)

Un+1 = Un - ¦¢(Un) (3.4)

Полученное соотношение поясняется графически на рис.3.6

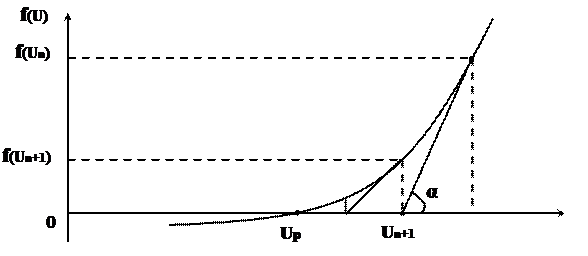Рис. 3.6.

Из рис. 3.6 следует

,

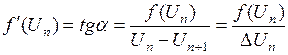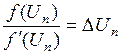и .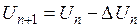

В результате метода последовательных приближений получается решение с заданной точностью.

Рассмотрим простейший пример диодной цепи рис. 3.4 б. Запишем первый закон Кирхгофа в дискретной форме

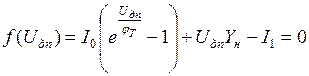. (3.5)

Производная от функции f(U_n)

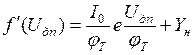(3.6)

Для получения итерационного процесса необходимо выражения (3.5) и (3.6) подставить в (3.4)

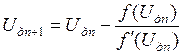. (3.7)

Начальное значение напряжения на диоде в (3.7) Uдo выбирается произвольно.

В общем случае для системы n нелинейных уравнений метод Ньютона – Рафсона можно записать в матричном виде:

® ® -1 ® ®

Un+1 = Un - J F (Un)

где

, ,

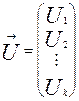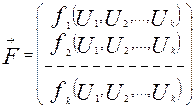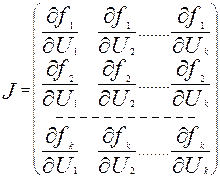(3.8)

Матрица (3.8) называется Якобианом.

В результате решения системы нелинейных уравнений получаем напряжение во всех узлах схемы и токи во всех ее ветвях при заданном постоянном входном воздействии, т.е. речь идет об анализе по постоянному току.

Частотный анализ справедлив только для линейных цепей, поэтому для его проведения необходимо линеаризовать схему в окрестностях рабочей точки.