Замечание. При дальнейшем изложении мы имеем в виду расположение рассматриваемых объектов в трехмерном пространстве

При дальнейшем изложении мы имеем в виду расположение рассматриваемых объектов в трехмерном пространстве. Практически все сказанное будет верно и для плоского случая (более общего, чем рассмотренный выше). Дело в том, что параметрическое описание плоской кривой не накладывает никаких ограничений на ее расположение относительно координатных осей: кривая не обязана однозначно проектироваться на координатную ось, как это имеет место в случае ее явного задания у = у(х). В частности, кривая может быть замкнутой, самопересекающейся и так далее. Все последующие построения законны и в этих сложных случаях.

Рассмотрим некоторые подходы к построению сглаживающей кривой. Пусть на плоскости или в пространстве задан упорядоченный набор точек, определяемых векторамиV₀, V₁,..., V_m (рис. 9). Ломаная V₀V₁...V_m называется контрольной ломаной, порожденной массивом V={V₀,V₁,...V_m} (рис. 10).

Кривой Безье, определяемой массивом V, называется кривая, определяемая векторным уравнением

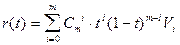, 0 £ t £ 1, (2)

где С_mⁱ = 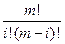коэффициенты в разложении бинома Ньютона (число сочетаний из m элементов по i).

Кривая Безье обладает замечательными свойствами:

• она является гладкой;

• начинается в точке V₀ и заканчивается в точке V_m, касаясь при этом отрезков V₀V₁ и V_m-1V_m контрольной ломаной;

• функциональные коэффициенты C_mⁱtⁱ(1-t)^m-i при вершинах V_i, i=0, I,..., m, суть универсальные многочлены (многочлены Бернштейна); они неотрицательны, и их сумма равна единице:

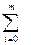C_mⁱtⁱ(1-t)^m-i = (t+(1-t))^m = 1

Поэтому кривая Безье целиком лежит в выпуклой оболочке, порождаемой массивом (рис. 11).

При m = 3 получаем (элементарную) кубическую кривую Безье, определяемую четверкой точек V₀, V₁, V₂, V₃ и описываемую векторным параметрическим уравнением

r(t)-(((l - t)V₀+3tV₁)(l - t) + 3t²V₂)(1 - t)+t³V₃, 0 £ t £ 1,

или, в матричной записи, r(t)= VMT, 0 £ t £ 1

где 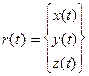V= (V₀ V₁ V₂ V₃) =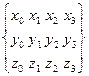

M = 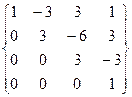, T =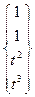

Матрица M называется базисной матрицей кубической кривой Безье.

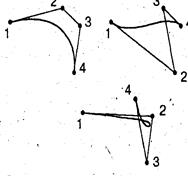
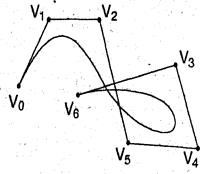
Порядок точек в заданном наборе существенно влияет на вид элементарной кривой Безье.

На рис. 12 построены элементарные кубические кривые Безье, порожденные наборами четверок точек, которые различаются только нумерацией. Нетрудно заметить, что, находясь в одной и той же выпуклой оболочке и пытаясь повторить контрольную ломаную в гладком варианте, эти кривые заметно разнятся.

Наряду с отмеченными достоинствами кривые Безье обладают и определенными недостатками.

Основных недостатков у элементарных кривых Безье три:

1) степень функциональных коэффициентов напрямую связана с количеством точек в заданном наборе (на единицу меньше);

2) при добавлении хотя бы одной точки в заданный набор необходимо провести полный пересчет функциональных коэффициентов в параметрическом уравнении кривой;

3) изменение хотя бы одной точки приводит к заметному изменению вида всей кривой.

В практических вычислениях часто оказывается удобным пользоваться кривыми, составленными из элементарных кривых Безье, как правило кубических.