Знаки неравенств “³” и "£ " определяются в результате подстановки координат вершин гиперплоскости в уравнение гиперплоскости. При этом используется свойство вершин принадлежать области работоспособности. Символ "£” соответствует отрицательному знаку результата подстановки, символ “³” - положительному. Для удобства использования результатов построения области работоспособности все неравенства приводятся к виду “³0”.
1.2.1. Пример построения области работоспособности и расчета попадания точки в заданную область
Задана таблица работоспособности объекта
Таблица 1
| № п/п | x1 | x2 | работоспособность объекта |
| да | |||
| да | |||
| да | |||
| да | |||
| да | |||
| да | |||
| да |
Вопрос: будет ли работоспособен объект с данными параметрами 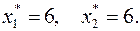
Решение. Геометрическое представление исходных данных.
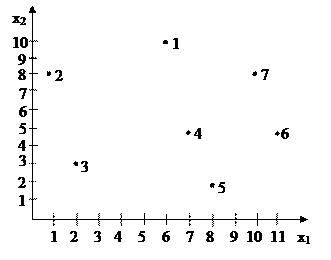
Рис.1.4. Координаты исходных данных
Проведем построение области согласно алгоритму, изложенному выше.
1 шаг. Берется (N + 1) точки в N – мерном пространстве в нашем случае N=2, т.е.берем точки 1, 2, 3.
Через каждые N точек проводится гиперплоскость и заполняется таблица
Таблица 2
| Прямая | 1 – 2 | 2 – 3 | 1 – 3 |
| Вершина | |||
| координаты вершин | 2; 3 | 6; 10 | 1; 8 |
| координаты 1-ой точки | 6; 10 | 1; 8 | 6; 10 |
| координаты 2-ой точки | 1; 8 | 2; 3 | 2; 3 |
| уравнение прямой | x1–2,5x2+19=0 | x1+0,2x2–2,6=0 | 7x1–4x2–2=0 |
2 шаг. Для точки 4 ищем генеральную гиперплоскость среди всех ранее построенных плоскостей. Является ли (1–2) генеральной гиперплоскостью для точки 4.
S (т.4) = 7 – 2,5 × 5 + 19 > 0
S¢ (т.3) = 2 – 2,5 × 3 + 19 > 0, т.е. (1-2), не является для точки 4 генеральной гиперплоскостью.
Для т. 4 генеральная гиперплоскость (1-3);
S¢ (т.4) = 7 × 7 – 4,5 - 2 > 0
S¢ (т.2) = 7 × 1 – 4,8 - 2 < 0, т.е. (1-3), является для точки 4 генеральной гиперплоскостью.
Мы снова имеем (N+1) точку – это {1, 3, 4}.
Через каждые N точек проведем гиперплоскости (в данном случае прямые).
Для упрощения построения часть таблицы не заполняется.
| Прямая | 1 – 3 | 3 – 4 | 1 – 4 |
| Вершина |
После обработки каждой точки генеральная гиперплоскость и плоскости повторяющиеся (одни и те же плоскости в разных таблицах) вычеркиваются.
3 шаг. Для точки 5 генеральная гиперплоскость (1–4)
| Прямая | 1 – 4 | 4 – 5 | 1 – 5 |
| Вершина |
а также (3 – 4)
| Прямая | 3 – 4 | 3 – 5 | 5 – 4 |
| Вершина |
4 шаг. Для точки 6 генеральная гиперплоскость (1 – 5)
| Прямая | 1 – 5 | 5 – 6 | 1 – 6 |
| Вершина |
5 шаг. Для точки 7 генеральная гиперплоскость (1 – 6)
| Прямая | 1 – 6 | 6 – 7 | 7 – 1 |
| Вершина |
Получили границу области работоспособности:
(1 – 2) – (2 – 3) – (3 – 5) – (5 – 6) – (6 – 7) – (7 – 1).
Окончательный шаг. Для перехода от уравнений к неравенствам необходимо в линейную форму (левая часть равенства) поставить координаты вершины.
Если величина линейной формы положительна, то знак “=” заменяется на “³”, если же отрицательна то знак “=” заменяется на “£”.
Пример: (1 – 2): x1 – 2,5x2 + 19 = 0.
S¢(т.3) = 2 – 2,5 × 3 + 19 > 0.
Соответствующее неравенство имеет вид: x1 – 2,5x2 + 19 ³ 0.
Полученная область имеет вид, представленный на рис.1.5.
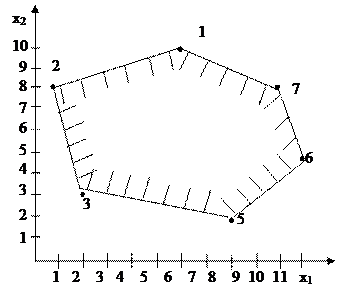
Рис.1.5. Область решений системы неравенств.
(1 – 2) Þ x1 – 2,5x2 + 19 ³ 0
(2 – 3) Þ x1 + 0,2x2 – 2,6 ³ 0
(3 – 5) Þ x1 + 6x2 - 20 ³ 0
(5 – 6) Þ -x1 + 0,75x2 + 6,5 ³ 0
(6 – 7) Þ -x1 – 0,5x2 +14 ³ 0
(7 – 1) Þ -x1 - 2x2 + 26 ³ 0
Проверка работоспособности объекта состоит в выполнении данных неравенств. Если хотя бы одно из неравенств не удовлетворяет условию, то точка не попадает в область.
Данная методика позволяет исключить сбойные результаты в экспериментах на основе адаптивных (последовательных) процедур. Адаптивность в данном случае означает отбрасывание случайных результатов до тех пор, пока численные характеристики случайной величины будут изменяться незначительно. Построение линейной гиперплоскости для большого числа переменных не представляет сложной задачи и решается методами линейной алгебры.
1.2.2. Пример удаления сбойных результатов
Для работы открыть файл or_teach.exe. В открывшемся поле системы координат ввести любые 4 точки, определяющие выпуклый четырехугольник (координаты точек записать в тетрадь). Внутрь полученного четырехугольника случайным образом ввести 4 точки, координаты которых также записать в тетрадь. Допустим, координаты полученных восьми точек следующие: {1 (73;127), 2 (190;126), 3 (84;204), 4 (217;224), 5 (115;139), 6 (94;162), 7 (153;169), 8 (179;214)}. Подсчитать средние значения координат x и y. В нашем случае xср = 138 и yср = 303 (округленные до целых значений).
Далее ввести точку, которая будет расположена за границами четырехугольника (например, точку 9 (152;43)). С учетом этой точки вычислим средние значения xcp1 = 140 и ycp1 = 282. Отбросим граничные точки: 1,2,3,4,9. Вычислим средние значения координат оставшихся точек 5,6,7,8: xcp2 = 135 и ycp2 = 274. Сравнить результат с первоначальным.
На рис.7 изображено множество точек из некоторой области. Видно, что точка 54 дает сбойный результат. Данный метод с удалением выпуклых оболочек (выпуклых слоев) предложил Тьюки. Процедура получила название «шелушение». Она позволяет при большом количестве точек измерения эффективно удалять сбойные результаты для объектов высокой размерности и, таким образом вести адаптивную обработку данных в задаче принятия решения о работоспособности объекта. При этом при вводе данных в программу or_teach.exe необходимо преобразовать исходные значения переменных Xисход. данных в координаты машинные Xмаш. По формуле линейного масштабного преобразования:
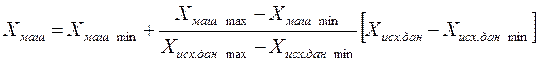 .
.
Например, Хисх.дан =Хисх.дан max, тогда Хмаш=Хмаш max;
Хисх.дан =Хисх.дан min, тогда Хмаш =Хмаш min.
Для учебных целей (рис.1.6) примем Хмаш max =300, Хмаш min =50.
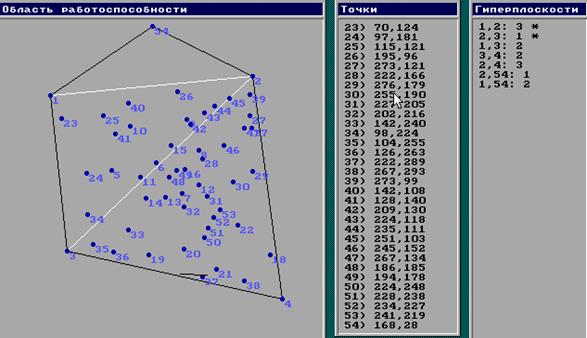
Рис1. 6. Исключение сбойных результатов методом Тьюки.
Рассмотрим теперь пример определения попадания точки с заданными координатами (х1;х2) в полученную область. Для этого открыть Windows-приложение MS Excel.
Все необходимые данные занести в таблицу, как показано на рис.1.7.
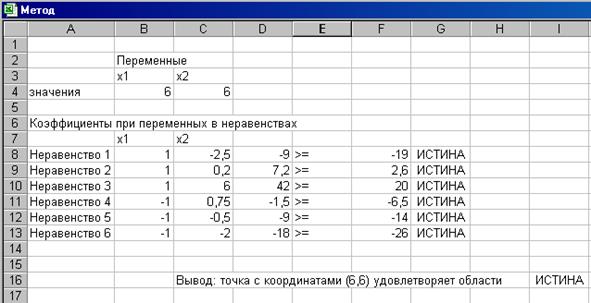
Рис. 1.7. Рабочее окно пакета MS Excel.
В ячейках B4 и C4 записаны координаты заданной точки.
Для неравенства 1 в ячейке В8 и С8 записаны коэффициенты при переменных х1 и х2 соответственно. В ячейку F8 занесен свободный коэффициент, причем необходимо учесть, что все неравенства записаны в виде Ах1+Вх2³С. В ячейке D8 записана формула подстановки точки (6;6) в линейную форму первого неравенства: 6*1+6*(-2,5)=-9. В обозначениях редактора электронных таблиц Excel данная формула будет выглядеть следующим образом: =суммпроизв($B$4:$C$4;B8:C8).
В ячейке Е8 проставлен знак неравенства 1, а в ячейку G8 занесена формула, =D8>=F8, вычисляющая логическую функцию со значениями ИСТИНА или ЛОЖЬ. Формулу в ячейке Е8 необходимо скопировать в ячейки Е9:Е13.
Окончательный результат записывается в ячейке I16 в виде формулы =И(G8:G13). То есть если во всех ячейках столбца G записано значение ИСТИНА, то, значит, точка попадает в данную область. Если же хотя бы оно из значений в столбце G принимает значение ЛОЖЬ, то результатом значения в ячейке I16 будет ЛОЖЬ. Это означает непопадание точки в данную область.
Изложенный алгоритм может служить основой для построения информационных систем контроля объектов. Пакет MS Excel позволяет реализовать алгоритм контроля для достаточно сложных объектов.
Содержание отчета по разделу №4
1. Краткое описание алгоритма описания области системой линейных неравенств.
2. Результаты описания области с различными масштабами.
3. Выводы.
Глава 5. Адаптивное построение модели регрессии при наличии сильной корреляции независимых факторов
Наличие корреляции независимых факторов в модели (4.1) и определение оценок вектора 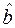 на основе соотношения (4.2) приводят к неустойчивости решения.
на основе соотношения (4.2) приводят к неустойчивости решения.
В этом случае при выполнении операции обращения матрицы в выражении (4.2) следует применять псевдообращение [4]:
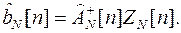 (4.9)
(4.9)
5.1. Определение псевдообратной матрицы А+(1,1) для произвольной матрицы А(1,1) на основе метода ортогонализации Грамма-Шмидта (ГШО)
1. Столбцы матрицы А(1,1), которые обозначим 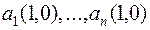 , преобразуются методом ГШО в ортогональные векторы (не обязательно, чтобы они получились ортонормированными). Из множества этих векторов образуется матрица
, преобразуются методом ГШО в ортогональные векторы (не обязательно, чтобы они получились ортонормированными). Из множества этих векторов образуется матрица 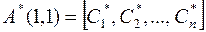 .
.
Ортогонализация столбцов матрицы методом ГШО производится по уравнениям 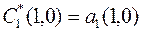 ;
;
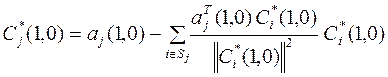 , (4.15)
, (4.15)
где 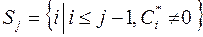 .
.
Здесь 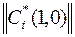 - норма вектора, определяемая выражением
- норма вектора, определяемая выражением 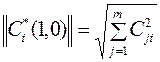 .
.
Сравнивая нормы векторов 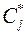 , принимают решение об обнулении вектора с малой нормой.
, принимают решение об обнулении вектора с малой нормой.
2. Столбцы 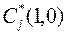 матрицы
матрицы 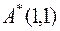 переставляются с помощью матрицы перестановок
переставляются с помощью матрицы перестановок 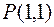 таким образом, что
таким образом, что
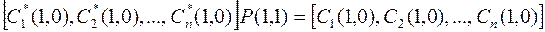 ,(4.16)
,(4.16)
где 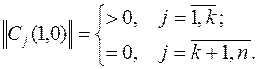
Матрица перестановок 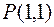 может быть подобрана следующим образом. Если требуется поменять местами i – столбец и j – столбец, то в единичной
может быть подобрана следующим образом. Если требуется поменять местами i – столбец и j – столбец, то в единичной 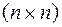 - матрице
- матрице 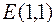 нужно сделать следующие замены:
нужно сделать следующие замены: 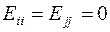 ;
; 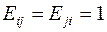 . В общем случае матрица
. В общем случае матрица 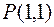 в (9.2) может включать произведение нескольких перестановочных матриц.
в (9.2) может включать произведение нескольких перестановочных матриц.
3. Столбцы 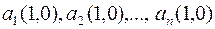 исходной матрицы А(1,1) переставляются с помощью матрицы перестановок Р(1,1), применяемой в п.2. При этом получают новую матрицу со столбцами, которые обозначим, например, так:
исходной матрицы А(1,1) переставляются с помощью матрицы перестановок Р(1,1), применяемой в п.2. При этом получают новую матрицу со столбцами, которые обозначим, например, так:
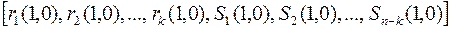 ;
;
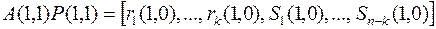 .
.
4. Вычисляются \вспомогательные коэффициенты
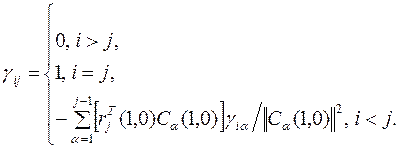
5. Вычисляется матрица В(1,1) размером 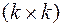 с элементами
с элементами
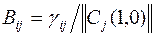
6. Вычисляется матрица U(1,1) размером 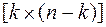 с элементами
с элементами
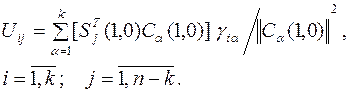
7. Вспомогательная матрица 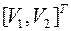 находится методом ГШО из столбцов матрицы
находится методом ГШО из столбцов матрицы 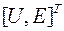 , т.е. к столбцам матрицы, сформированной из двух матриц U(1,1), E(1,1), применяют процедуру, аналогичную процедуре (4.15), но с тем отличием, что после получения каждого ортогонального вектора, начиная с первого вектора, его нормируют путем деления всех компонентов вектора на его норму. Условно эту процедуру можно представить в виде следующей цепочки преобразований:
, т.е. к столбцам матрицы, сформированной из двух матриц U(1,1), E(1,1), применяют процедуру, аналогичную процедуре (4.15), но с тем отличием, что после получения каждого ортогонального вектора, начиная с первого вектора, его нормируют путем деления всех компонентов вектора на его норму. Условно эту процедуру можно представить в виде следующей цепочки преобразований:
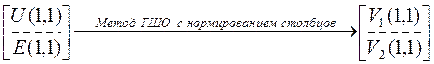
Здесь размер матриц 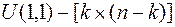 ;
;
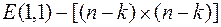 ;
; 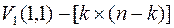 ;
; 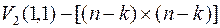
8. Вычисляется матрица 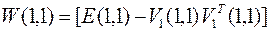 .
.
9. Используя матрицу, полученную в (4.15), вычисляем матрицу
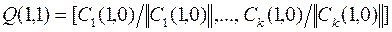 .
.
10. С помощью вспомогательных матриц B(1,1), U(1,1), W(1,1), Q(1,1), P(1,1), вычисленных в пп. 2, 5, 6, 8, 9, определяется псевдообратная матрица
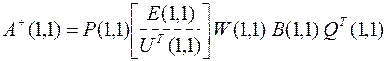
Оценка коэффициентов линейной регрессии определяется выражением 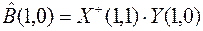 .
.
Пример 1. Получение устойчивого решения системы линейных уравнений на основе использования псевдообратных матриц.
Система уравнений имеет вид

Её точное решение: 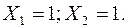
Рассмотрим систему с измененной правой частью:
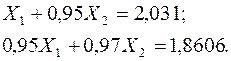
Её точное решение: 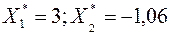 , т.е. решение неустойчиво.
, т.е. решение неустойчиво.
Исследуем матрицу системы на обусловленность. Матрица А(1,1) в данном случае симметрична. Тогда на основании того, что 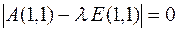 имеем
имеем
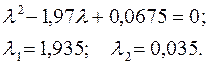
Обусловленность матрицы 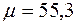 , т.е. матрица системы плохо обусловлена и необходимо применять методы повышения устойчивости решения. Рассмотрим два метода.
, т.е. матрица системы плохо обусловлена и необходимо применять методы повышения устойчивости решения. Рассмотрим два метода.
Построение псевдообратной матрицы для симметричной матрицы. Используя уравнения 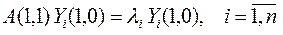 , определяем собственные векторы матрицы
, определяем собственные векторы матрицы
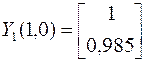 ;
; 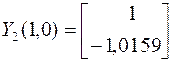 .
.
После нормировки
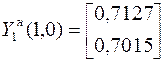 ;
; 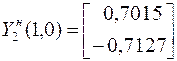 .
.
На основании соотношения
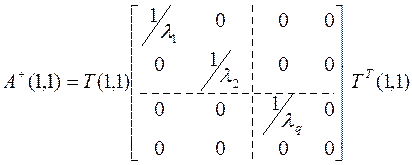
определяем псевдообратную матрицу (в примере примем q=1).
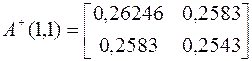 .
.
Решение при «точных» данных
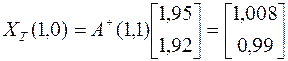 .
.
Решение при измененной правой части
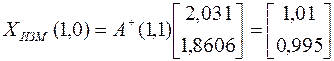 .
.
Из полученных результатов видно, что решение задачи с помощью псевдообращения становится менее чувствительным к ошибкам (изменениям) исходных данных.
Построение псевдообратной матрицы на основе метода ортогонализации Грамма-Шмидта.
1. Используя (4.15), определяем ортогональные векторы
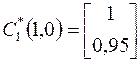 ;
; 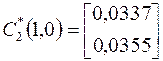 ;
;
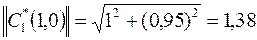 ;
; 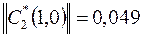 .
.
Сравнивая нормы, принимаем решение, что второй вектор исходной матрицы 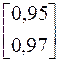 является линейно зависящим от первого вектора
является линейно зависящим от первого вектора 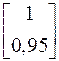 и им можно пренебречь, т.е.
и им можно пренебречь, т.е. 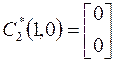 .
.
2. Таким образом, число независимых столбцов k=1.
Матрица перестановок 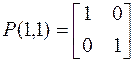 .
.
3. 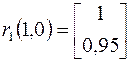 ;
; 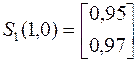 .
.
4. 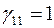 .
.
5. B=0,7246.
6. U=0,9837.
7. 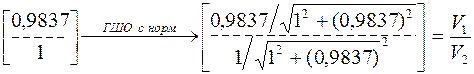 .
.
8. W=0,5082.
9. 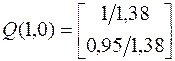 .
.
10. 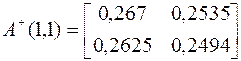 .
.
Решение при «точных» данных
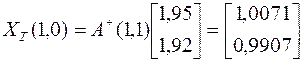 .
.
Решение при измененной правой части
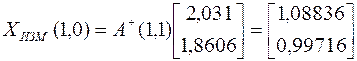 ,
,
т.е. полученные решения являются более устойчивым по сравнению с теми, которые не используют псевдообращение матриц.
5.2. Решение линейных многомерно-матричных уравнений на основе псевдообращения многомерной матрицы
Многоиндексные задачи линейного оценивания можно формализовать в виде многомерно-матричных уравнений
Y(p,0) = H(p,q)X(q,0) + V(p,0) (4.10)
где X(q,0) – столбец оцениваемых характеристик или массивов; Y(p,0) – столбец наблюдений или измерений; H(p,q) – известная матрица преобразования; V(p,0) – столбец ошибок измерений.
Матрица H+(q,p) может быть выражена через сингулярное разложение матрицы H(p,q).
Прямое и обратное сингулярные преобразования многомерной матрицы имеют вид
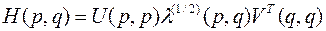 , (4.11)
, (4.11)
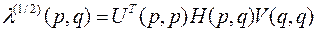 , (4.12)
, (4.12)
где U(p,p), V(q,q) – многомерные ортогональные матрицы собственных элементов для матриц H(p,q)HT(p,q) и HT(p,q) H(p,q) соответственно; l1/2(p,q) – диагональная многомерная матрица сингулярных чисел H(p,q). Выражение для псевдообращения H(p,q) через сингулярное разложение запишется в виде
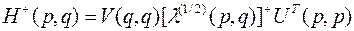 (4.13)
(4.13)
Псевдообращение диагональных элементов l1/2(p,q) означает вычисление их обратных значений, а для «нулевых» элементов (величина «нулевых» элементов меньше некоторого малого числа t) результат псевдообращения будет равен нулю. Основная трудность вычисления псевдообратной матрицы через сингулярное разложение заключается в нахождении матриц U(p,p), V(q,q). После определения многомерной псевдообратной матрицы псевдорешение многомерного уравнения (4.10) находится в виде
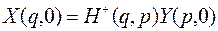 (4.16)
(4.16)
Это решение минимизирует норму
½½Y(p,0) – H(p,q)X(q,0)½½.
Адаптивное оценивание параметров модели регрессии при наличии аномальных результатов измерений.
В реальных системах обработки информации оценки 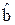 вектора регрессионных коэффициентов b для модели
вектора регрессионных коэффициентов b для модели
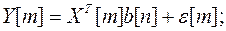
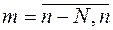 (4.1)
(4.1)
(X[m] – вектор наблюдаемых линейно независимых факторов;
b – вектор неизвестных и подлежащих оценке параметров;
e[m] – помеха типа белого шума) приходится проводить в условиях аномальных измерений (АИ) Y(l), l Î (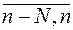 ).
).
Наибольшее распространение при решении поставленной задачи получили методы максимального правдоподобия при известном законе распределения ошибки и метод наименьших модулей, обеспечивающий устойчивое решение в условиях отклонения реального закона распределения ошибки от постулируемого априори закона распределения [7,10]. Однако все эти методы требуют в случае обнаружения АИ значительных вычислительных затрат для исключения влияния самих измерений на искомую регрессионную зависимость.
В пособии предлагается организовать процесс вычислений таким образом, чтобы не получать каждый раз результат заново, а корректировать процесс вычислений с учетом аномальности результата измерений. Подобный подход можно применять для обработки как накопленных данных, так и последовательно поступающей порции информации.
4.1. Метод выделения результата АИ
В основу алгоритма положен итеративный метод решения на основе МНМ. При этом оценка 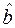 , полученная на основе N результатов измерения, имеет вид
, полученная на основе N результатов измерения, имеет вид
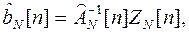 (4.2)
(4.2)
где
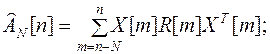 (4.3)
(4.3)
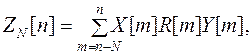 (4.4)
(4.4)
где 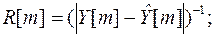
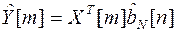 - оценка m-го измерения выходного сигнала.
- оценка m-го измерения выходного сигнала.
Начальные значения R[m]=1; 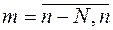 соответствуют определению параметров
соответствуют определению параметров 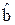 по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (4.2) – (4.4) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[ l ] указывает на наиболее грубое l-измерение.
по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (4.2) – (4.4) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[ l ] указывает на наиболее грубое l-измерение.
4.2. Рекуррентная процедура исключения АИ
Матрицу 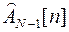 и вектор Zn-1[n] при R[m]=1;
и вектор Zn-1[n] при R[m]=1; 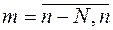 можно определить из
можно определить из 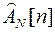 , ZN[n] полученных на первой итерации, путем исключения аномальных составляющих
, ZN[n] полученных на первой итерации, путем исключения аномальных составляющих

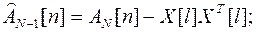 (4.5)
(4.5)
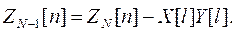 (4.6)
(4.6)
На основании леммы об обращении матриц можно записать
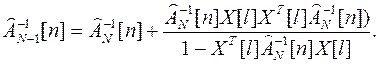 (4.7)
(4.7)
Используя выражения (4.6) и (4.7), получим
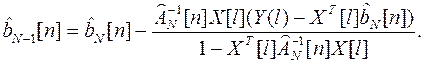 (4.8)
(4.8)
4.3. Рекуррентная процедура учета текущего неаномального измерения
Эта процедура соответствует обычному рекуррентному МНК с нарастающей памятью.
Рекуррентные расчетные соотношения имеют вид:
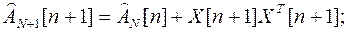
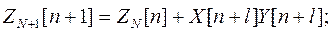
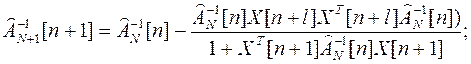
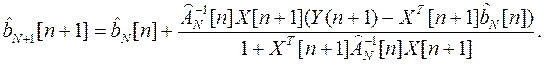
При большом числе измерений итерационную процедуру проверки на аномальность очередного измерения следует начинать с весовой функции
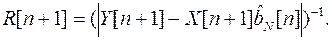
В ряде случаев достаточно проверки
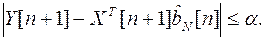
Величина a определяется статистическими характеристиками помехи.
Глава 6. Определение главных компонент дискретного конечного множества элементов
6.1. Определение первого главного компонента
J=N
У1 =∑ W1J*XJ
J=0
X0=1
W1J(K+1)= W1J(K)+
a * У1 [XJ(K)- W1J(K)*Y1(K)]
Коэффициент a обозначает коэффициент обучения. Он оказывает существенное влияние на сходимость алгоритма.
В процессе обучения сети одни и те же обучающие выборки предъявляются вплоть до стабилизации весов сети.
6.2. Последовательное определение множества главных компонентов в векторной форме
W2(K+1)= W2(K)+a * У2(K) [X**(K)- W2(K)*Y2(K)]
Для второго нейрона (второго главного компонента)
X**(K)=[X(K)- W1(K)*Y1(K)].
В этой формуле присутствуют только уже известные веса первого нейрона.
Аналогично для третьего нейрона
W3(K+1)= W3(K)+ a * У3(K) [X**(K)- W3(K)*Y3(K)]
X**(K)=[X(K)- W1(K)*Y1(K)- W2(K)*Y2(K)].
6.3. Модификация алгоритма
1. Входной и выходной слои имеют одинаковую размерность:
X1 X апр 1
X2 Xапр2
X3 Xапр3
XN XапрN
2. Скрытый слой определяется числом главных компонент M<N.
Недостаток структуры: все нейроны подстраиваются одновременно.
Пример 1.
| x1 | НС-ГЛ_Комп | |||||||
| x2 | ||||||||
| W | Y=w*x | |||||||
| 0,447213 | 0,894427 | 2,236068 | 2,236068 | 6,708203 | 8,944271 | 15,65247 | ||
| wT= | 0,447213 | |||||||
| 0,894427 | ||||||||
| WT*Y= | 2,999999 | 3,999998 | 6,999997 | |||||
| X-XA= | 4,5E-07 | 4,5E-07 | 1,35E-06 | 1,8E-06 | 3,15E-06 | |||
| 1,04E-07 | 1,04E-07 | 3,13E-07 | 4,17E-07 | 7,3E-07 | ||||
| (X-XA)^2= | 2,03E-13 | 2,03E-13 | 1,83E-12 | 3,24E-12 | 9,94E-12 | |||
| 1,09E-14 | 1,09E-14 | 9,79E-14 | 1,74E-13 | 5,33E-13 | ||||
| критерий= | 1,62E-11 | |||||||
| (сумE^2) |
Пример 2.
| x1 | |||||||
| x2 | |||||||
| x3 | |||||||
| x4 | |||||||
| W | |||||||
| -0,21737 | -0,43475 | 0,211961 | 0,847826 | ||||
| 0,390828 | 0,781658 | 0,117885 | 0,471557 | ||||
| Y | |||||||
| 9,722922 | 29,16877 | 53,64739 | 29,85403 | 8,978673 | |||
| 7,966477 | 23,89943 | 47,7489 | 39,63252 | 17,78717 | |||
| WT | -0,21737 | 0,390828 | |||||
| -0,43475 | 0,781658 | ||||||
| 0,211961 | 0,117885 | ||||||
| 0,847826 | 0,471557 | ||||||
| WT*Y= | 1,000006 | 3,000019 | 7,000029 | 8,999995 | 4,999989 | ||
| 2,000003 | 6,000009 | 14,00001 | 9,999993 | ||||
| 3,000009 | 9,000028 | 17,00004 | 10,99997 | 3,999966 | |||
| 35,99999 | 67,99998 | 44,00001 | 16,00001 | ||||
| (X-Xa)^2= | 4,03E-11 | 3,62E-10 | 8,4E-10 | 2,18E-11 | 1,15E-10 | ||
| 9,61E-12 | 8,65E-11 | 1,84E-10 | 2,12E-11 | 4,68E-11 | |||
| 8,93E-11 | 8,04E-10 | 1,33E-09 | 1,13E-09 | 1,18E-09 | |||
| 2,4E-11 | 2,16E-10 | 4,34E-10 | 9,36E-11 | 1,55E-10 | |||
| Крит= | 7,18E-09 | ||||||
| (сумма) | |||||||
6.4. Построение опорных векторов
Опорные векторы являются теми точками данных, которые ближе всего лежат к поверхности решений.

Выбор центров кластеризации осуществляется на основе метода оптимума номинала и проверки статистических гипотез.
Метод оптимизации номинала.
Необходимо найти точку внутри области примерно на равном расстоянии от границы области. В большинстве случаев применяется квадратичный критерий.
Исходная система ограничений:
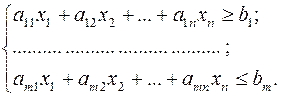 (*)
(*)
Левые части обозначим:
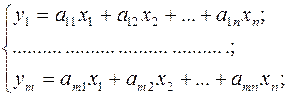
Берём у1 как целевую функцию и на множестве (*) находим максимальное и минимальное значения у1. Затем берем у2 и опять находим максимальное и минимальное значения у2 и т.д. (yi min, yi max).
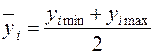 - среднее значение.
- среднее значение.
Тогда система ограничений примет вид:
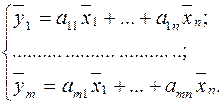
Это система линейных алгебраических уравнений.
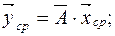
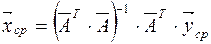 .
.
Пример.
Имеется система ограничений:
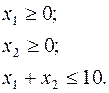
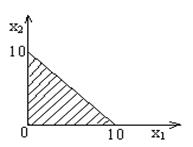
Обозначим левые части:
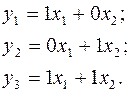
Средние значения: 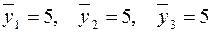 , так как max=10, min=0.
, так как max=10, min=0.
Вместо уi подставляем 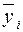 :
:
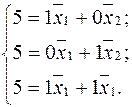
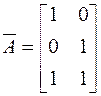
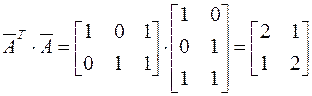
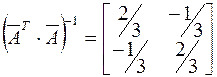
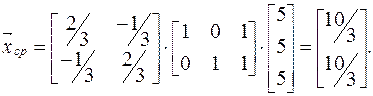
Решение: 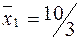 ,
, 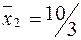 .
.
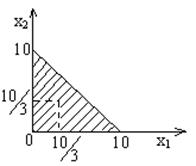
Глава 7. Адаптивный итеративный метод восстановления входного сигнала измерительной системы
Для уравнения (2.8) итерационная процедура может быть представлена в виде [6]:
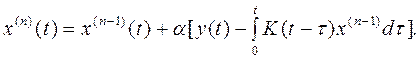 (3.1)
(3.1)
Выбор величины α обеспечивается сходимостью в среднем к решению уравнения (2.8). Дифференцирующие звенья принципиально не могут быть реализованы с большой точностью, интегрирующие инерционные звенья принципиально могут быть реализованы с любой заданной точностью, поэтому для восстановления входного сигнала целесообразно использовать итерационную процедуру
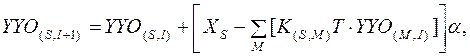 (7)
(7)
где Т (шаг интегрирования) и a определяются точностью интегрирования, К – матрица преобразования интегрирующего оператора, для примера S = 0…7, M = =0…7, I = 1…2000 (число итераций). За счет выбора малого значения a= 0,1 обеспечиваем сходимость итерационной процедуры. Итерационная процедура записана для реализации в пакете MATHCAD.
Пример 1. Восстановление входного сигнала интегрирующего звена  с помощью итерационных процедур.
с помощью итерационных процедур.
Начальные значения входного сигнала принимаются равными выходному сигналу.
Входной сигнал: XT = [1 2 3 4 3 2 1 1].
Выходной сигнал: YT = [0,1 0,3 0,6 1 1,3 1,5 1,6 1,7]. T=0,1, a=0,1.
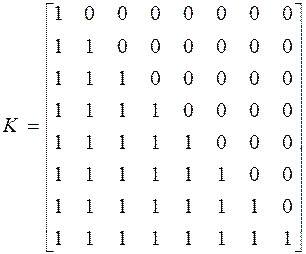 .
.
восстановленный сигнал 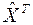 = [1 2 3 4 3 2 1 1].
= [1 2 3 4 3 2 1 1].
Пример 2. Восстановление входного сигнала апериодического звена 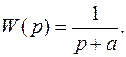
Для восстановления входного сигнала используем итерационную процедуру (3.2). Начальные значения входного сигнала принимаются равными выходному сигналу. Импульсная переходная функция рассчитывается по формуле K(t) = e–t. Матрица преобразования имеет вид
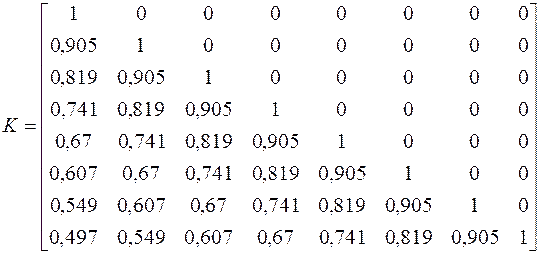 .
.
Входной сигнал ХТ = [1 2 3 4 3 2 1 1].
Выходной сигнал: YT = [0,1 0,29 0,563 0,909 1,123 1,216 1,2 1,186]. T=0,1, a = 0,1.
Восстановленный входной сигнал после 2000-й итерации
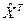 = [1 2 3 4 3 2 1 1].
= [1 2 3 4 3 2 1 1].
Некоторого упрощения итерационной процедуры можно добиться, если, применять БПФ-свертку без двоичных инверсий (пример вычисления БПФ-свертки дан в разделе 2.2.1.)
7.1. Оптимальная коррекция динамических погрешностей измерений
В данном пособии принята на интервале наблюдения модель входного сигнала полиномиального типа
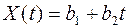 . (3.3)
. (3.3)
В качестве моделей линейной динамической измерительной системы приняты передаточные функции вида:
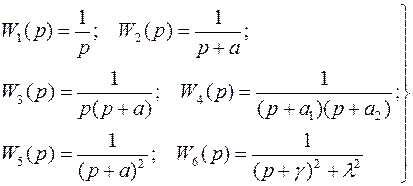
 (3.4)
(3.4)
с помощью которых могут быть описаны различные классы измерительных систем. Расчетная схема формирования наблюдаемого сигнала системы оптимальной коррекции динамических погрешностей измерений системой W(p) представлена на рис. 3.1.
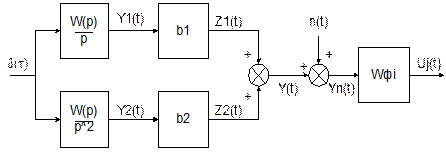
Рис. 3.1. Схема оптимальной фильтрации при наличии помехи типа «белый шум»
Необходимо синтезировать линейные фильтры Wfi, i=1,2, выделяющие с наименьшей дисперсией ошибки из выходного сигнала измерительной системы Yn(t) составляющие, пропорциональные контролируемым параметрам b1,b2,…,bn. Сигналы Z1(t), Z2(t) (рис. 3.1) являются случайными из-за случайности параметров b1,b2. Желаемым выходным сигналом mj(t) синтезируемого линейного фильтра Wfj является сигнал
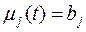 . (3.5)
. (3.5)
Сформируем ошибку при определении параметра bj с помощью фильтра Wfj в виде
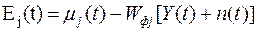 (3.6)
(3.6)
и определим оператор Wfj из условия минимума дисперсии этой ошибки
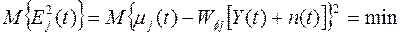 . (3.7)
. (3.7)
Рассмотрим вначале решение данной задачи для случая помехи n(t) типа «белого шума» с корреляционной функцией Rn(t) = n*d(|t|). Затем на основе данного решения произведем обобщение на случай произвольной помехи.
Оптимальные несмещенные оценки 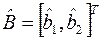 в случае помехи типа «белого шума» определяются соотношением:
в случае помехи типа «белого шума» определяются соотношением:
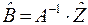 . (3.8)
. (3.8)
Элементы матрицы А и вектора 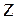 равны
равны
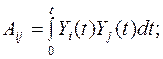 (3.9)
(3.9)
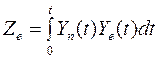 . (3.10)
. (3.10)
Точность оценок характеризуется дисперсионной матрицей ошибок
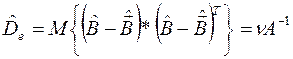 , (3.11)
, (3.11)
где n – интенсивность белого шума.
В случае дискретных измерений выходного сигнала измерительной системы в моменты t=nT уравнения (3.9), (3.10) перепишутся в виде
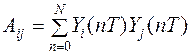 , (3.12)
, (3.12)
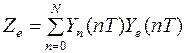 . (3.14)
. (3.14)
Синтезируем на основе рассмотренной схемы рис. 3.1 оптимальный фильтр в случае помехи, отличной от «белого шума».
Преобразуем расчетную схему, представленную на рис. 3.2. Помеха n(t) характеризуется нулевым математическим ожиданием и корреляционной функцией Rn(t). Будем искать оптимальный фильтр в виде последовательного соединения двух звеньев F1 и F2j, j=1,2. Звено F1 такое, что преобразует стационарную произвольную помеху n(t) в стационарный «белый шум». Эквивалентная расчетная схема представлена на рис. 3.2.
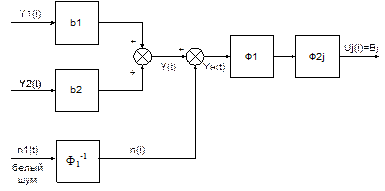
|
Здесь F1-1 представляет собой формирующий фильтр для помехи n(t) c корреляционной функцией Rn(t). Окончательно схему (рис. 3.2) можно представить в виде рис. 3.3.
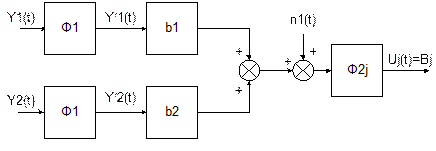
|
Таким образом, рассмотренная выше методика синтеза оптимальных фильтров может быть применена и для случая синтеза фильтров при произвольной помехе.
Глава 8. Нейронная сеть Хопфильда
Сеть Хопфильда подобна памяти, которая может вспомнить сохраненный образец по подсказке, представляющей собой искаженную помехами версию нужного образца.
Весовые значения сети Хопфильда: W= 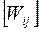
Первый столбец представляет весовые значения, связанные c первым элементом нейронной сети. Столбец 2-весовые значения, связанные со вторым элементом.
Когда элемент обновляется, его состояние изменяется в соответствии с правило Sj=sgn(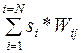 )
)
Работа сети.
Входной вектор задает начальные состояния всех элементов.
Элемент для обновления выбирается случайным образом.
Выбранный элемент получает взвешенные сигналы от всех остальных элементов Sj=sgn(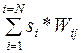 ) и изменяет свое состояние.
) и изменяет свое состояние.
Выбирается другой элемент и процесс повторяется до установившегося состояния.
Весовая матрица, соответствующая ”сохранению” векторов Xi, задается формулой:W= 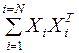 , в которой все диагональные элементы должны быть установлены равными нулю (поскольку диагональные элементы задают автосвязи, а элементы сами с собой, естественно, не связаны).
, в которой все диагональные элементы должны быть установлены равными нулю (поскольку диагональные элементы задают автосвязи, а элементы сами с собой, естественно, не связаны).
Сеть Хопфильда
№1. 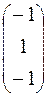
№2. 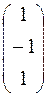
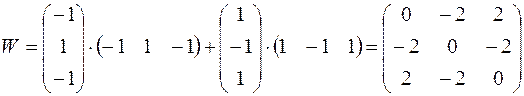
Диагональные элементы обнулены
Работа сети.
Случайная последовательность обработки нейронов:
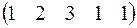
на выходе 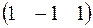
Сначала рассмотрим элемент S1
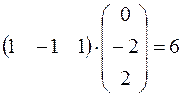
S1=1
То есть первый нейрон сохранил свое значение
Теперь рассмотрим элемент S2
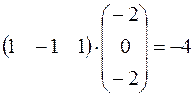
S2= –1
То есть второй нейрон сохранил свое значение
Теперь рассмотрим элемент S3
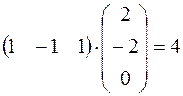
S3=1
То есть третий нейрон сохранил свое значение.
Таким образом, сеть Хопфильда считает, что на вход нейронной сети подан второй вектор (из двух сданных на хранение).
Глава 9. Нечеткие нейронные сети
9.1. Общая схема модели управления в условиях неопределенности
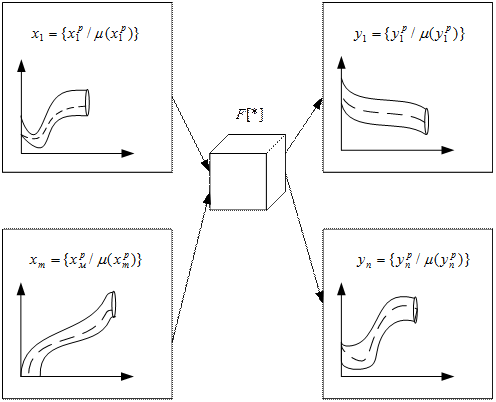
Рис. 1. Общая схема модели управления в условиях неопределенности
Первый слой нейронов формирует с помощью функции принадлежности значения данного измерения. Для аппроксимации функции принадлежности целесообразно применять радиальные нейронные сети.
Второй слой формирует принадлежности преобразованных нечетких переменных с помощью преобразователя F (рис.1).
Модели являются практически единой альтернативой в социологии, долгосрочных прогнозах (погода, медицина, макроэкономика). В последнее время информационные модели (ИМ) широко используются и при изучении технических и инженерных систем. В ряде случаев информационные и математические компоненты могут составлять единую модель (например, внешние условия описываются решениями уравнений математической физики, а отклик системы – информационной моделью).
Основным принципом ИМ является принцип ЧЯ (черного ящика). В противоположность аналитическому подходу, при котором моделируется внутренняя структура системы, в методе ЧЯ моделируется внешнее функционирование системы. Сточки зрения пользователя, структура модели системы, спрятанная в ЧЯ, имитирует поведенческие особенности системы. Кибернетический принцип ЧЯ был предложен в рамках теории идентификации систем, в которой для построения модели системы предлагается широкий параметрический класс базисных функций или уравнений, а сама модель синтезируется путем выбора параметров при условии наилучшего, при заданной функции ценности, соответствия решений уравнений обращения системы. При этом структура системы никак не отражается в структуре уравнений модели.
При разработке ИМ очень важным является выбор информационного базиса. В большом количестве случаев принято, что таким базисом являются искусственные нейронные сети, которые, как показано в, являются удобным и естественным базисом для представления ИМ. НС может быть формально определена как совокупность простых процессорных элементов (в данном случае нейронов), которые обладают целиком локальным функционированием и объединены однонаправленными связями (синапсами).
Укажем, что для рассматриваемых случаев УН, в качестве элементов информационного базиса в задачах прогнозирования используется нечеткий нейрон (собственно процессорный элемент), который может иметь довольно сложный алгоритм функционирования, включающий операции НМа. Связями такогонейрона с другими нейронами может быть жгут (или трубка) синапсов. Сеть принимает некоторый входной сигнал из внешнего мира и пропускает его сквозь себя с превращениями в каждом процессорном элементе. Таким образом, в процессе прохождения сигнала по связям сети происходит его обработка, результатом которой является определенный выходной сигнал. В обобщенном виде НС выполняет функциональное соответствие между входом и выходом и может служить ИМ G системы S.
Обусловленная НС функция (или оператор) могут быть произвольными при легко осуществимых требованиях к структурной сложности сети и наличия нелинейности в Передаточных (активационных) функциях нейронов. При моделировании реальных сложных систем значения функции системы S или оператора F[*] определяются на основе экспериментов или наблюдений, которые проводятся лишь для конечного числа параметров х. При этом значения как x, так и y измеряются приблизительно, и подвергнуты ошибкам разной природы (т. н. «мягкие вычисления»).
Цель моделирования - получение значений системных откликов при произвольном изменении х. В этой ситуации в условиях определенности (например, статистической) может быть успешно применена информационная (статистическая) модель G исследуемой системы S. Укажем, что ИМ для задач управления в условиях определенности могут строиться на основе традиционных методов непараметрической статистики. Эта наука позволяет строить обоснованные модели систем в случае большого набора экспериментальных данных (достаточного для доказательства статистических гипотез о характере распределения) и при относительно равномерном их распределении в пространстве параметров. Однако при высокой стоимости экспериментальных данных, или невозможности получения достаточного их количества (как, например, при построении моделей сложных производственных аварий, пожаров и т. п.), или их высокой зашумленности, неполноте и противоречивости такие модели являются неработоспособными. В особенности опасно использование этих моделей при малых статистических выборках, так как полученные на них законы распределения могут быть неустойчивыми, т.е. при увеличении (уменьшении) количества элементов выборки закон распределения может принципиально изменяться. На это впервые обратил внимание академик Ю. В. Линник.
В таких условиях наилучшими оказываются НС модели. Они выборочно чувствительны в областях сосредоточения данных и дают гладкую интерполяцию в других областях. Применяя любой метод моделирования, всегда нужно оценить степень точности модели и характер приближений. Специфичность ИМ обнаруживается не только в способах их синтеза, но и в характере сделанных приближений и соответственно, связанных сними ошибок. Определяют такие главные отличия в обращении системы и ее ИМ, которые нужно учитывать и которые возникают вследствие свойств экспериментальных данных.
Информационные модели по своей природе всегда являются неполными. Пространства входных - выходных переменных в общем случае, не могут содержать все важные для описания параметры системы. Это связано как с техническими ограничениями, так неограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных увеличиваются требования к объему экспериментальных данных, необходимых для построения модели. Эффект неучтенных (скрытых) параметров может повлиять на однозначность моделирования системы S.
База экспериментальных данных, на которых основывается модель G, рассматривается как база внешних данных. При этом в данных всегда присутствуют ошибки разной природы, шумы, а также противоречия отдельных измерений друг другу. За исключением простых случаев, противоречия в данных не могут быть устранены.
Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задач. Как следствие, получаемые модели будут иметь неодинаковую достоверность и точность в разных областях изменения параметров.
Экспериментальные данные могут содержать изъятые значения (например, вследствие потери информации, отказа датчиков, невозможности проведения полного набора экспериментов и т.п.). Произвол в интерпретации этих значений, опять-таки, ухудшает свойства модели. Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам ИМ.
9.2 Концепция измерений, основанная на подходе Заде. Понятие о нечетких множествах
3.1.Понятия о нечетких множествах.
переменная = 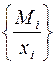 , можно xi ставить в числителе.
, можно xi ставить в числителе.
Пример
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
1. Мало
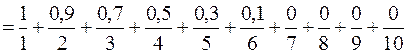 ;
;
2. Очень мало 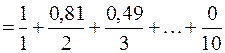 ;
;
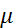 ОЧЕНЬ МАЛО = (µмало)2
ОЧЕНЬ МАЛО = (µмало)2
3. Немало 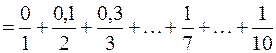
m немало =1-m мало
4. 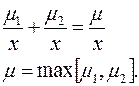
5. y=f(x), f – четкий функциональный преобразователь, x – нечеткая переменная.
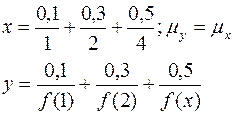
6. y1=f (x, y), f - четкий функциональный преобразователь, x, y – нечеткие переменные.
µy1 = µx^µy
Ù - означает минимум
Например, 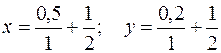

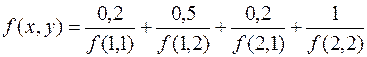
f(x, y) – это, например, x+y; x/y; x*y; и т.д.
3.2. Примеры формирования нечетких множеств
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Мало =
 2015-05-30
2015-05-30 657
657







