2015-05-22
937
Введение в теорию множеств
Не существует строгого определения множества.
Определение 1. Под множеством понимают всякое собрание каких-либо объектов.
Определение создателя теории множеств Г. Кантора: «Множество – есть многое, мыслимое нами как единое. Объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью».
Примеры. 1) А = {множество студентов в группе}, 2) N = {множество натуральных чисел}.
Определение 2. Объекты, из которых состоят множества, называются элементами.
Если а – элемент множества А, то пишут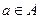 
– а принадлежит А.
Множества сами могут быть элементами множеств. Например, множество натуральных чисел – элемент множества целых чисел. Большинство множеств не являются элементами самих себя. Например, множество всех котов не является элементом самого себя, потому что оно само не кот.
Если все элементы множества А – числа, то А – числовое множество.
Числовые множества
Первоначальные данные о числе относятся к эпохе каменного века – палеомелита. Это «один», «мало» и «много». Записывались они в виде зарубок, узелков и т.д. Развитие трудовых процессов и появление собственности заставили человека изобрести числа и их названия.
1) Первыми появились натуральные числа N, получаемые при счете предметов.
Множество натуральных чисел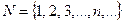 
– числа для счета предметов.
2) Затем, наряду с необходимостью счета, у людей появилась потребность измерять длины, площади, объемы, время и другие величины, где приходилось учитывать и части употребляемой меры. Так возникли дроби. Формальное обоснование понятий дробного и отрицательного числа было осуществлено в 19 веке. Множество целых чисел Z – это натуральные числа, натуральные со знаком минус и нуль.
Множество целых чисел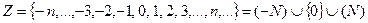 
3) Целые числа и дробные образовали совокупность рациональных чисел Q, но и она оказалась недостаточной для изучения непрерывно изменяющихся переменных величин.
Множество рациональных чисел – Q
4) Бытие снова показало несовершенство математики: невозможность решить уравнение вида х 2 = 3, в связи с чем появились иррациональные числа I.
Множество иррациональных чисел I – бесконечные непериодические десятичные дроби
5) Объединение множества рациональных чисел Q и иррациональных чисел I – множество действительных (или вещественных) чисел R. В итоге числовая прямая заполнилась: каждому действительному числу соответствовала на ней точка.
Множество действительных чисел –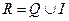 
6) На множестве R нет возможности решить уравнение вида х 2 = – а 2. Следовательно, снова возникла необходимость расширения понятия числа. Так в 1545 году появились комплексные числа. Их создатель Дж. Кардано называл их «чисто отрицательными». Название «мнимые» ввел в 1637 году француз Р. Декарт. Лишь к концу 18 – началу 19 века комплексные числа заняли достойное место в математическом анализе.
Множество комплексных чисел – С.
