Схема Бернулли

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться (то есть появится событие 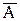). При этом вероятность события А в каждом испытании одна и та же и равна р. Требуется вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие А наступит ровно k раз (безразлично в какой последовательности) равна:

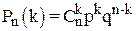, где q=1– p.

Локальная формула Муавра-Лапласа. Если число независимых испытаний велико, а вероятность появления события А в каждом из них постоянна и равна p (0 < p < 1), то вероятность того, что в n независимых испытаниях, событие наступит ровно k раз (безразлично в какой последовательности), приближенно равна (тем точнее, чем больше n):

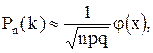
где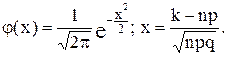

Значения функции 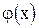можно найти с помощью таблицы 2 приложения. Данная формула, в отличие от формулы Бернулли, используется при больших n и k.

Интегральная теорема Лапласа. Если число независимых испытаний велико, а вероятность появления события А в каждом из них постоянна и равна p (0 < p < 1), то вероятность того, что в n независимых испытаниях событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P_n(k₁ 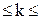k₂)» Ф(x ^²) – Ф(x^¢),

где 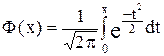– функция Лапласа (смотри приложение);

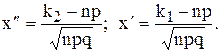
Замечание. Если функция Лапласа задана выражением:

Ф*(x)= 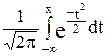, то Ф*(x) = 0,5 + Ф(x).

Пример. Игральная кость брошена четыре раза. Найти вероятность того, что шестерка появится не более двух раз.

Решение:

Пусть событие В - шестерка появится не более двух раз. В является суммой несовместных событий

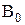– шестерка не появится ни разу;

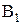– шестерка появится ровно один раз;

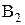– шестерка появится ровно два раза.

Вероятность события можно найти по формуле Бернулли. Рассуждаем так.

Произведенное испытание – бросание игральной кости.

Событие А (успех) – выпадение шестерки. Событие 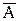(неудача) – выпадение любого числа очков, кроме шести. По классическому определению вероятности имеем:

.

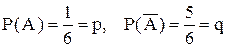Таких испытаний, согласно условию, производится четыре. Тогда вероятность того, что в 4-х независимых испытаниях будет 0 успехов, найдем так:

.

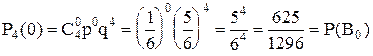Аналогично рассуждая, получим:

,

.

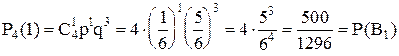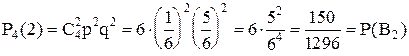Используя теорему сложения несовместных событий, получим:

= .

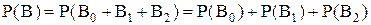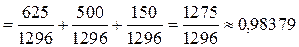Пример. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более, чем на 0,04.

Решение. По условию задачи задано, что: n=625; p=0,8; e=0,04.

Отсюда q =1– p = 0,2. Требуется найти вероятность:

?

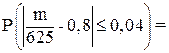Для решения указанной задачи воспользуемся формулой, определяющей оценку отклонения относительной частоты от постоянной вероятности, т.е.:

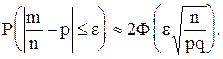
Ф(х) – интегральная функция Лапласа. Найдем аргумент функции Лапласа:

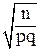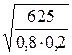х = e =0,04 =2,5

По таблице 3 приложения для функции Лапласа найдем, что Ф(2,5)=0,4983, т.е. 2Ф(х)=0,9876. Итак, искомая вероятность:

P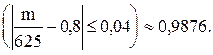

ЗАДАЧИ

1.Монета бросается 5 раз. Какова вероятность того, что герб появится:

а) ровно 3 раза;

б) не более двух раз;

в) хотя бы один раз.

г) Что вероятнее: выиграть у равносильного противника 2 партии в шахматы из пяти или 3 из семи?

2.Вероятность выживания бактерий после радиоактивного облучения равна 0.004. Найти вероятность того, что после облучения из 500 бактерий останется не менее 3 бактерий.

3.Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0.004. Найти вероятность того, что в течение одной минуты обрыв произойдет на пяти веретенах.

4.Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0.02. Какое из двух событий вероятнее: в течение одной минуты позвонит 3 абонента или 4 абонента?

5.На факультете учатся 500 студентов. Найти вероятность того, что первое сентября является днем рождения:

а) трех студентов; б) не менее трех студентов.

6.Вероятность появления события в каждом из независимых испытаний равна 0.2. Найти вероятность того, что событие наступит 20 раз в 100 испытаниях.

7.Монета бросается 100 раз. Вычислить вероятность того, что число появлений герба будет заключаться между 40 и 60.

8.Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0.2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребуют ремонта; б) хотя бы один потребует ремонта.

9.Игральная кость подброшена 200 раз. Найти вероятность того, что цифра «6» выпала более 30 раз, но не более 40 раз.

10.Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0.01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных.