1. Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Гомоморфизм и изоморфизм групп.
Среди алгебраических систем важнейшую роль играют группы.
Определение: Не пустое множество G с какой-то ассоциативной операцией *, которое является и обратимой называется группой.
Пример: <A, *>
1) a*(b*c)=(c*a)*b
2) a*x=b, x*a=b
Однако, проверить обратимость операции бывает достаточно сложно, поэтому проверка группы проводится по следующим правилам: < A, +>, a,b,c, 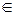 A
A
1) a*b
2) 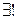 (квантор существует и он единственный)
(квантор существует и он единственный)
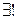 e
e 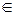 A, a*e=e*a=a, e-нейтральный элемент.
A, a*e=e*a=a, e-нейтральный элемент.
Когда e=0, это аддитивная запись, т. к. сложение
Когда e=1 – мультипликативная запись, так как умножение.
3) 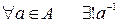 Существует симметричный элемент
Существует симметричный элемент 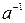 или (-a)
или (-a)
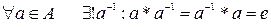 мультипликативная
мультипликативная
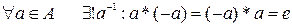 аддитивная запись
аддитивная запись
4) (a*b)*c=a*(b*c) свойство ассоциативности
Пример: (множество натуральных чисел с операцией +)-<N,+>
Определение: Группа называется коммутативной, если выполняется свойство коммутативности: a*b=b*a
Пусть множество G является группой относительно некоторой операции. Подмножество H 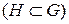 в котором выполняются свойства 1-4 относительно той же операции называется подгруппой.
в котором выполняются свойства 1-4 относительно той же операции называется подгруппой.
|
|
|
То есть, множество H также является группой относительно той же операции звездочка (*).
Из определения следует, что любая группа является своей подгруппой и что любое множество состоящее только из единицы группы так же будет ее подгруппой.
Множество положительных рациональных чисел является группой относительно операции умножения и одновременно является подгруппой мультипликативной группы положительных действительных чисел.
Для того, чтобы установить, что непустое подмножеств H группы G есть подгруппа этой группы достаточно проверить два условия:
1) a,b 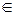 H, то a*b
H, то a*b 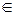 H (где звездочка (*) – любая операция), например: ½+½=1/1б т.е Q=1/1
H (где звездочка (*) – любая операция), например: ½+½=1/1б т.е Q=1/1
2) a 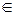 H, то
H, то 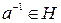 , пример: 2/3*3/2=1, где а=2/3 и
, пример: 2/3*3/2=1, где а=2/3 и 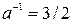
Эти условия можно заменить одним условием: Для любых элементов принадлежащих H: a,b 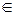 H,
H, 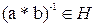

Отображением группы G на множество G’(G штрих) с одной операцией называется гомоморфизмом если это отображение сохраняет операцию, то есть для любых элементов группы a,b 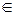 G из условия:
G из условия: 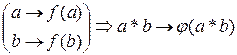
Пример: <N,+> и <R,*>
Пусть даны два множества A и A’ (A штрих)
<A,0>, <A’,*>
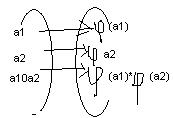
<A,0> <A’,*>
Теорема: Гомоморфный образ группы так же является группой относительно своей операции.
При гомоморфизме единицы группы G отображаются в единицы группы G’, а взаимнообратные элементы из G отображаются во взаимообратные элементы G’.
Если гомоморфное отображение взаимооднозначно, то оно называется изоморфным или изоморфизмом.
Изоморфные группы можно считать совпадающими.
2. Кольца. Примеры колец. Простейшие свойства кольца. Подкольца. Гомоморфизм и изоморфизм колец.
|
|
|
Множество действительных чисел R является группой относительно операции сложения, причем эта группа коммутативна, то есть выполняются следующие свойства:
- (a+b)+c=b+(c+a) свойство ассоциативности
- a+b=b+a свойство коммутативности
- a+x=b это уравнение имеет единственное решение.
Кроме того, операция сложения связана с операцией умножения двумя законами дистрибутивности:
- a(b+c)=ab+ac
(a+c)b=ba+bc
Операция умножения обладает свойством пять:
- a(bc)=(ab)c
Множество K с операцией сложения, умножения называется кольцом, если для любых элементов a,b,c  K выполняются свойства 1-5.
K выполняются свойства 1-5.
Пример: Множество квадратных матриц порядка n является кольцом относительно операции умножения и сложения матриц. Множество целых чисел относительно операции сложения и умножения чисел.
Свойства колец:
Будем использовать аддитивную терминологию (по сложению). Нейтральный элемент равен нулю, а противоположный (-a)
- –(-a)=a
- a-b=a+(-b)
- –a-b=(-a)+(-b)
- a-a=0
- a(b-c)=ab-ac или (b-c)a=ba-ca
- a*0=0 или 0*a=0
- (-a)b=-ab, a(-b)=-ab, -a*(-b)=ab
Отличные от нуля элементы a и b? Произведение которых равно 0 называют делителями нуля.
Пример: 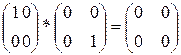 -эти матрицы называют делителями нуля.
-эти матрицы называют делителями нуля.
Подмножество M кольца R называется подкольцом, если оно само является кольцом при тех же операциях сложения т умножения, которые определены в кольце R.
Пример: Кольцо четных целых чисел является подкольцом кольца целых чисел, а кольцо целых чисел является подкольцом кольца рациональных чисел.
Теорема: Для того, чтобы не пустое подмножество M кольца К,было его подкольцом необходимо и достаточно, чтобы сумма, разность и произведение двух любых из M также принадлежало множеству M (чтобы не выйти за пределы этого множества).
Пусть R1 и R2 произвольные кольца, если R2 является образом кольца R1 то:
- Образ нуля R1 кольца при отображении переходит в ноль кольца R2.
- Единица из R1 переходит в единицу из R2.
- Для всякого элемента a кольца R1 образ элемента противоположного элементу a равен элементу противоположному образу элементу x.
Два кольца R1 и R2 называются изоморфными, если R1-гомоморфна R2, a R2-гомоморфна R1.
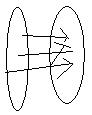 - гомоморфизм
- гомоморфизм 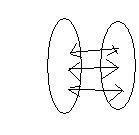 - изоморфизм
- изоморфизм
3. Алгебры, алгебраические системы.
Свойства операций состоит в следующем: двум элементам из некоторого множества соответствует некоторый третий элемент.
Картеж -упорядоченный набор из n-элементов.
Операцией над множеством a называется отображение, соответствующее каждому картежу <a1>,<a2>… из A определенный элемент этого же множества.
Операции будем обозначать *, 0 и т.п.
Определение: Всякое множество с заданными в нем операциями будем называть алгебраическими множествами.
Пример: <N,+> и <R,*>
Пусть даны два множества A и A’ (A штрих)
<A,0>, <A’,*>

<A,0> <A’,*>
Отображение системы A на A’ (штрих) сохраняющее операции называется гомоморфизмом, при этом система A’ является гомоморфным образом системы A.
Пример: Множество целых чисел Z с операцией сложения и множество действительных чисел на отрезке [-1;1] с операцией умножения. Эти две системы являются гомоморфными.
Гомоморфное отображение A на систему A’, при котором множество A первой системы отображается на множество A’ второй системы взаимооднозначно называется изоморфизмом.
Пример: Множество действительных чисел с операцией сложения и множество диагональных матриц второго порядка с операцией сложения:
Пример: A<R,+>; A’< 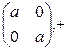 >
>
a,b
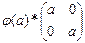
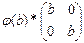
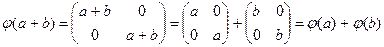
Изоморфные алгебраические системы отличаются лишь такими признаками, которые связаны с конкретной природой элементов и операций. Во всем остальном изоморфные системы не различимы - любое утверждение, которое формируется только с помощью равенств связывающих элементы и операции истинно или ложно одновременно для каждой изоморфной системы.
В системе с одной операцией звездочка(*) имеется такой нейтральный элемент, что композиция произвольного элемента a и нейтрального элемента равна элементу a.
|
|
|
Пример: 1. <R,+>,2. < 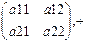 >, 3. <Q,*>, 4.множество поворотов на угол
>, 3. <Q,*>, 4.множество поворотов на угол 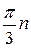 .
.
1. a 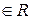 , a+0=a;
, a+0=a;
2. 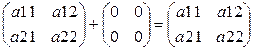 ; 3.
; 3. 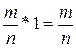 ; 4.
; 4.  - множество поворотов на 120 градусов, 360 и т.д.
- множество поворотов на 120 градусов, 360 и т.д.
4. Поле. Примеры полей. Простейшие свойства поля.
Дано множество для произвольных элементов которого выполняются свойства:
- a+(b+c)=(a+b)+с ассоциативность
- a+b=b+a коммутативность
- a+x=b единственное решение
- a(b+c)=ab+ac или (b+c)a=ba+ca дистрибутивность
- a(bc)=(ab)c
- ab=ba
- ax=b единственное решение
Множество P с операциями сложения и умножения называется полем, если в P содержатся элементы, отличные от нуля для которых выполняются свойства 1-7.
Поле является кольцом, для которого выполняются дополнительные требования 6-7, поэтому все свойства колец будут справедливы и для полей.
Пример: Множество рациональных чисел с обычными операциями сложения и умножения являются полем, а множество целых чисел относительно обычных операций сложения и умножения не являются, где не выполняется 7 свойство:
2х=7
Х=7/2-не целое число.
Свойства полей:
- –(-a)=a
- a-b=a+(-b)
- –a-b=(-a)+(-b)
- a-a=0
- a(b-c)=ab-ac или (b-c)a=ba-ca
- a*0=0 или 0*a=0
- (-a)b=-ab, a(-b)=-ab, -a*(-b)=ab
Специфические свойства полей (нет в кольцах):
- Поле не содержит делителя нуля. Если
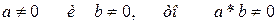
- Подмножество не нулевых элементов поля является коммутативной группой относительно операции умножения. Из этого свойства вытекают следствия:
- всякое поле содержит нейтральный элемент относительно операции умножения.
- вместе с каждым не нулевым элементом поле содержит единственный обратный ему элемент.
3. В любом поле выполняются следующие равенства:
а) (-a)=(-1)*a
б) b/a=b* 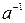
в) 1/(ab)= 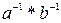
г) 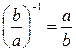
д) 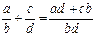
5. Числовое поле. Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа.
Дано множество для произвольных элементов которого выполняются свойства:
- a+(b+c)=(a+b)+с ассоциативность
- a+b=b+a коммутативность
- a+x=b единственное решение
- a(b+c)=ab+ac или (b+c)a=ba+ca дистрибутивность
- a(bc)=(ab)c
- ab=ba
- ax=b единственное решение
Множество P с операциями сложения и умножения называется полем, если в P содержатся элементы, отличные от нуля для которых выполняются свойства 1-7.
|
|
|
Поле является кольцом, для которого выполняются дополнительные требования 6-7, поэтому все свойства колец будут справедливы и для полей.
Замечание:
В поле любой ненулевой элемент обратим, поэтому можно определить операцию деления и частного двух элементов.
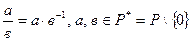 , где Р – поле.
, где Р – поле.
Свойства:
1. 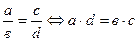
2. 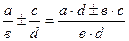
3. 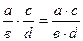
4. 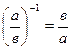
Числовые поля:
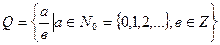 , < Q, +, ×> – поле;
, < Q, +, ×> – поле;
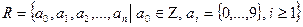 , R=< R, +, ×> - поле;
, R=< R, +, ×> - поле;
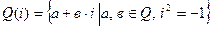 , < Q(i), +, × > - поле гауссовых чисел;
, < Q(i), +, × > - поле гауссовых чисел;
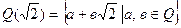 , < Q(
, < Q(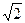 ), +, ×> - квадратичное поле.
), +, ×> - квадратичное поле.
Существуют различные способы построения комплексных чисел. Рассмотрим следующий подход, где комплексное число интегрируется как пара действительных чисел.
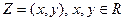
1* z1 + z2 = (x1y1)+(x2y2) = (x1 + x2, y1 + y2)
2* z1×z2 = (x1y1)×(x2y2) = (x1x2 – y2y1, x1y2 + x2y1)
Теорема: Алгебра С = < C z{z=(x, y), x,y 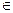 R}, +, × > - поле.
R}, +, × > - поле.
(x, 0) = x (обозначим действительную часть)
(0, 1) = i (обозначим мнимую единицу)
i2 = (0, 1)×(0, 1) = (-1, 0) = -1 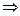 i2= -1/
i2= -1/
(0, y) = (y, 0)×(0,1) = y×i (обозначим);
z = (x, y) = (x, 0) + (0, y) = x + i×y
|
комплексного числа.
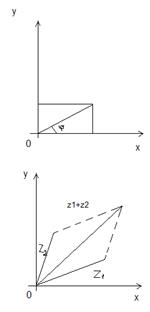 Геометрическое представление комплексных чисел и операций над ними.
Геометрическое представление комплексных чисел и операций над ними.
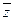
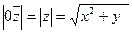 - модуль комплексного числа
- модуль комплексного числа
j - аргумент комплексного числа;
|
j определен с точностью до 2πк, и аргумент
0 не определен.
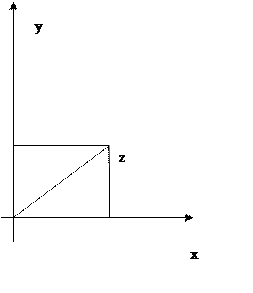
Геометрическая интерпретация сложения комплексных чисел
Геометрическая интерпретация
Противоположного комплексного
числа
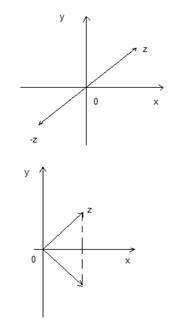 Геометрическая интерпретация сопряженного комплексного числа
Геометрическая интерпретация сопряженного комплексного числа
Тригонометрическая форма комплексного числа.
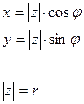
z= x+ iy = 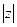 (
(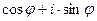 )
)

z= r×(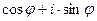 ) тригонометрическая запись комплексного числа
) тригонометрическая запись комплексного числа
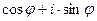 =
= 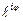 (обозначим)
(обозначим)
z = r× 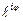 - показательная форма записи комплексного числа.
- показательная форма записи комплексного числа.
Свойства операций над комплексными числами, записанными в тригонометрической форме.

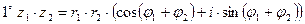

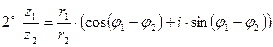

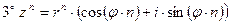

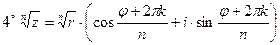 ,
, 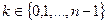
 2015-06-04
2015-06-04 1453
1453