Если функция 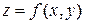 дифференцируема в точке
дифференцируема в точке 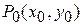 , то, как было показано выше, ее полное приращение в этой точке можно представить в виде
, то, как было показано выше, ее полное приращение в этой точке можно представить в виде
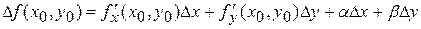 .
.
Сумма первых двух слагаемых есть главная линейная (относительно 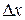 и
и 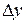 ) часть приращения функции.
) часть приращения функции.
Определение. Если функция 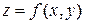 дифференцируема в точке
дифференцируема в точке 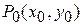 , то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается
, то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается
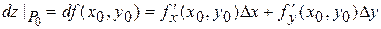 .
.
Приращения независимых переменных 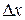 и
и 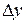 называют дифференциалами независимых переменных
называют дифференциалами независимых переменных 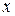 и
и 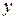 и обозначают соответственно
и обозначают соответственно 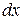 и
и 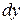 . Тогда полный дифференциал функции можно записать в виде:
. Тогда полный дифференциал функции можно записать в виде:
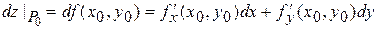
или в более краткой форме: 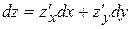 .
.
Пример. Найти полный дифференциал функции 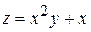 .
.
Решение. 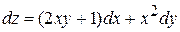 для
для 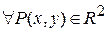 .
.
Пример. Найти полный дифференциал функции 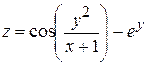 .
.
Решение. Найдем частные производные функции:
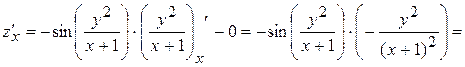
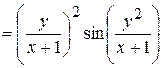 ,
,
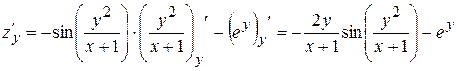 .
.
Следовательно,
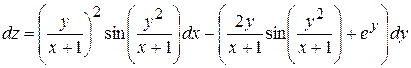
для 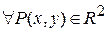 .
.
Определение полного дифференциала легко обобщается на случай функции любого числа переменных. Например, полным дифференциалом функции трех переменных 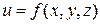 в точке
в точке 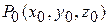 называется главная, линейная относительно приращений всех аргументов, часть полного приращения функции, т. е.
называется главная, линейная относительно приращений всех аргументов, часть полного приращения функции, т. е.
|
|
|
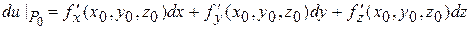 .
.
Из определения дифференциала функции нескольких переменных следует, что для функции 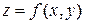 можно полагать
можно полагать 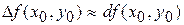 , а для функции
, а для функции 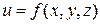 , зависящей от трех переменных
, зависящей от трех переменных 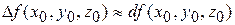 , для
, для 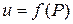 ,
, 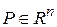
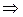
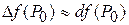 .
.
Эти соотношения позволяют получить формулы для приближенного вычисления значений функции:
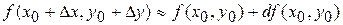 ,
,
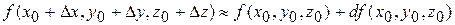 .
.
И в общем случае,
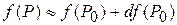 .
.
Полный дифференциал чаще используется для оценки погрешности вычислений по формулам.
Например, если задана дифференцируемая функция 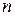 переменных
переменных 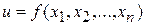 . Тогда абсолютная погрешность
. Тогда абсолютная погрешность 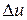 вычислений по этой формуле оценивается величиной
вычислений по этой формуле оценивается величиной
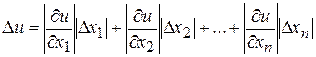 ,
,
а относительная погрешность ― величиной 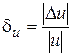 .
.
 2015-06-04
2015-06-04 720
720








