Методические указания по изучению темы «Корреляционное отношение. Нелинейная регрессия. Множественная и частная корреляция»

Из предыдущих занятий студенты должны были усвоить, что применимость 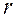базируется в основном на следующих двух условиях: 1) отношение между переменными линейно; 2) двумерное распределение гомоскедастично.

Однако важно знать, что очень часто исходные данные приводят к нелинейным моделям. В рамках данной темы как раз и рассматриваются математические методы, с помощью которых можно измерить криволинейные зависимости, изучаемые социологами. Один из них - это метод корреляционного отношения, который часто обозначается через 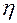(греческая строчная буква «эта»), но лучше выражается посредством .

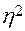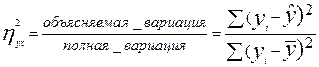, где 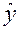- внутригрупповое среднее значение признака 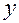; 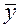- общее среднее арифметическое признака 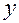. Данная формула представляет собой вычисление 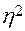для несгруппированных данных. В случае, если данные сгруппированы, эта формула выглядит следующим образом: .

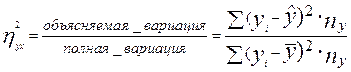Студенты должны запомнить, что для вычисления 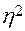необходимо найти среднее значение в каждом столбце (строке) корреляционной таблицы, общее среднее этих значений и отклонения средних значений для соответствующих колонок от общего среднего.

Для более эффективного усвоения материала данной темыследует провести сравнение статистических показателе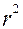й и :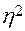

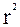= 0, есл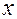и и 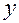независимы.

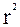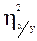= =1, тогда и только тогда, когда имеется строгая линейная связь между 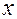и .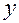

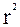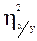£ – когда имеется строгая нелинейная функциональная зависимость 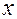и .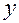

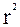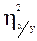= < 1 – когда регрессия 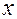и 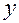строго линейная, но нет функциональной зависимости.

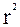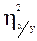< < 1 означает, что нет функциональной зависимости и существует нелинейная кривая регрессия.

Важно также знать, что в случае, когда 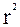£ 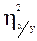– между признаками существует строгая нелинейная связь. Задача социолога отыскать уравнение функциональной зависимости, определяющее эту связь, то есть уравнение регрессии. В рамках курса «Математические методы в социологии» рассматриваются только два типа криволинейной зависимости: параболический и гиперболический. Соответствующие уравнения имеют следующий вид:

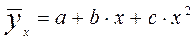-уравнение, определяющее параболу.

Для нахождения параметров a, b, c необходимо решить систему уравнений:

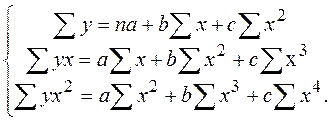
В случае если корреляционное поле представляет собой кривую, которая может быть описана гиперболой, поиск ее уравнения ведется по формуле: 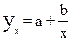. Для нахождения параметров a, b необходимо решить систему уравнений:

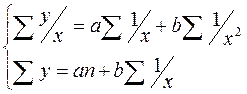- формулы для несгруппированных данных.

Студенты должны знать, что в социологической практике часто возникает необходимость в изучении влияния нескольких переменных 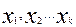на результирующий признак 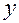. В этой связи нужно уметь строить регрессионное уравнение более общего вида, то есть 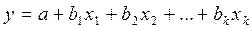, где 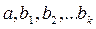-постоянные коэффициенты, называемые частными коэффициентами регрессии.

Следует рассмотреть пример построения двухфакторного регрессионного уравнения. Предположим, что изучается зависимость признака (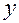) от признаков (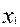) и (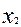). Нужно найти эту зависимость в виде линейного уравнения следующего вида: .

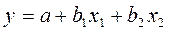При расчете коэффициентов уравнения множественной регрессии полезно преобразовать исходные эмпирические данные следующим образом:

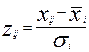, при этом уравнение множественной регрессии примет вид:

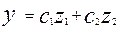, где с₁ и с₂ находятся из системы уравнений

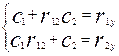, решая которую, получаем, что , ,

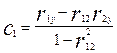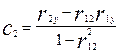где 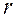- коэффициент парной корреляции между признакам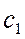и.

и 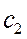называются стандартизированными коэффициентами регрессии. Следовательно, зная коэффициенты корреляции между изучаемыми признаками, можно подсчитать коэффициенты регрессии.

Коэффициенты 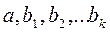исходного регрессионного уравнения находятся по формулам:

; ; .

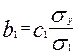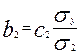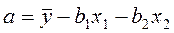Коэффициенты 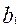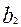_, можно рассматривать как показатели тесноты связи между переменными 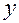и, например, 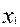,при постоянстве .

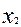Частный коэффициент корреляции - показатель, который характеризует тесноту и направление связи между результирующим признаком (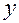) и факторным признаком (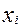) при элиминировании остальных признаков.

Частный коэффициент корреляции записывается 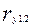и вычисляется по формуле: .

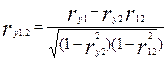Необходимо запомнить, что для определения степени связи результирующего признака 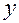с совокупностью независимых переменных вычисляется множественный коэффициент корреляции 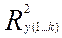, который иногда выражается в процентах и вычисляется по формуле:

1- .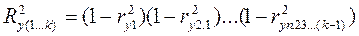

Важно также запомнить: множественный коэффициент корреляции показывает, что включение признаков 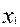и 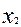в уравнение на определенное количество процентов объясняет изменчивость результирующего фактора. Чем больше 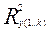, тем полнее независимые переменные 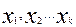описывают признак 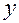. Обычно 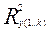служит критерием включения или исключения новой переменной в регрессионное уравнение. Если 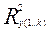мало изменяется при включении новой переменной в уравнение, то такая переменная отбрасывается.

В целом, для закрепления знаний, полученных в рамках изучения данной темы и выработки соответствующих практических навыков, на практическом занятии студентам предлагается решить ряд задач, условие которых предполагает вычисление корреляционного отношения, а также нахождение нелинейной регрессии и определение множественной и частной корреляции (по аналогии
с приведенным выше примером).

Вопросы и задания для самоконтроля

1. Допустимо ли вычисление 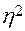, если линия регрессии плавная?

2. Можно ли вычислить 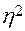для двух качественных переменных? Почему?

3. При каких табличных условиях числовые значения 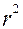и 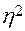совпадают?

4. Изобразите графически условия, при которых значение 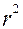приблизительно равнялось бы нулю, а 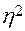=1,00.

5. Поясните, почему гомоскедастичность не может быть одинаковой
в обоих направлениях, если регрессия криволинейна? Изобразите графически.

6. Определите, что фиксирует частный коэффициент корреляции и каковы его свойства?

7. Опишите, для каких целей применяется множественный коэффициент корреляции?

Тема 10. Корреляция рангов: коэффициент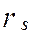

План

1. Измерение взаимосвязи признаков с помощью рангов.

2. Метод корреляции рангов (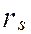) - коэффициент Спирмена.

3. Вычисление коэффициента Спирмена в случае объединенных рангов.

4. Коэффициент множественной корреляции качественных признаков.

5. Интерпретация коэффициентов ранговой корреляции.

Методические указания по изучению темы

«Корреляция рангов: коэффициент »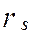

Следует уточнить, что на предыдущих занятиях использование корреляционных методов ограничивалось измерением связи между количественными переменными на основе совместимых частот. Однако студентам важно знать, что качественные переменные также могут быть связаны (тогда говорят, что они ковариантны). Из всего множества известных корреляционных индексов
в рамках данной темы рассматриваются только два – коэффициент парной ранговой корреляции (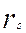) и (W) – коэффициент конкордации (определяющий степень множественной связи между качественными признаками). Коэффициент ранговой корреляции используется для измерения взаимозависимостей между качественными признаками, значения которых могут быть упорядочены или проранжированы по степени убывания (или возрастания) данного качества
у исследуемых социальных объектов.

Следует знать, что формула для измерения степени корреляции между двумя рядами рангов была выведена Спирменом в 1904 году. Студентам нужно запомнить эту формулу: ,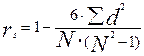

где: d - разность между парными рангами;

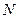- число ранжированных объектов.

Величина 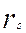может изменяться в пределах от +1 до –1, когда два ряда проранжированы в одном порядке. При полном взаимном беспорядочном расположении рангов 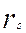равен нулю. Значимость коэффициента корреляции Спирмена для 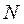£ 100 можно определить по таблице критических величин 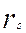. Если 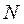> 100, то критические значения также находятся по таблице. При этом наблюдаемые значения критерия вычисляются по формуле: .

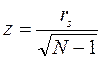Важно помнить, что ранги иногда могут объединяться. В таких случаях обоим наблюдениям приписывается значение среднего арифметического из двух объединенных рангов. Также необходимо понять, что 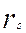измеряет корреляцию между порядковыми рангами, а не между ранжируемыми величинами.
В связи с этим нужно иметь в виду, что 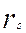преувеличивает степень связи между изучаемыми переменными.

Следует подчеркнуть тот факт, что формула для вычисления 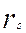пригодна только для двух ранговых рядов. Однако данные могут состоять из трех и более ранговых рядов. В такой ситуации одним из наиболее простых методов определения общей степени соответствия между тремя и более упорядоченными рядами данных является вычисление среднего арифметического из всех возможных значений 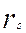. Результат подобной операции носит название «коэффициент конкордации» (соответствия).

Студенты должны иметь в виду, что когда усредняется очень много значений 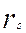, вычисления становятся более трудоемкими. Для таких случаев разработан очень простой метод усреднения значений 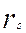, что имеет вид следующей формулы: 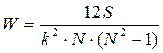, где 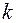- число переменных; 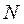- число индивидов или категорий, которые ранжируются; 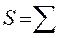(сумма рангов по строке - а)², а - среднее из суммы рангов. Важно помнить, что значимость полученной величины W для 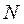> 7 проверяется по критерию 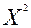: 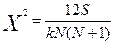со степенью свободы 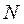-1.

Так как 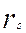применяется к порядковым данным, не имеющим определенных единиц измерения, этот показатель весьма полезен для социолога, которому часто приходится иметь дело с данными, носящими субъективный характер. Ранжирование предпочтений, эстетических суждений и других аналогичных явлений - все это можно коррелировать для того, чтобы определить степень согласия в предпочтениях респондентов и оценках экспертов.

В целом, для закрепления знаний, полученных в рамках изучения темы «Корреляция рангов: коэффициент 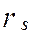», и выработки навыков определения корреляции качественных переменных, на практическом занятии студентам предлагается ряд задач социологического содержания, направленных на вычисление коэффициентов парной ранговой корреляции (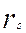) и коэффициента конкордации (W). Необходимо не только найти числовые значения этих коэффициентов, но и осуществить их социологическую интерпретацию в соответствии
с условием задачи.

Вопросы и задания для самоконтроля

1. Определите следующие понятия: ранг, ранговый порядок, равные интервалы, порядковые числа, корреляция ранговых последовательностей.

2. Укажите два серьезных затруднения в интерпретации рангов в качестве аналогов социальных явлений, которые они призваны отобразить.

3. При каких обстоятельствах могут быть ранжированы качественные данные?

4. Являются ли различия между соседними рангами непременно одинаковыми? Приведите пример.

5. Определите различие между соответствием и корреляцией.

6. Проверьте на примере тот факт, что объединенные ранги уменьшают корреляцию.

7. Опишите алгоритм вычисления коэффициента Спирмена.

8. Объясните принцип вычисления множественного коэффициента корреляции для ранговых рядов.

Тема 11. Коэффициент взаимной сопряженности. Некоторые общие
принципы интерпретации коэффициентов корреляции

План

1. Коэффициенты взаимной сопряженности для измерения связи между качественными признаками.

2. Вычисление коэффициента сопряженности К. Пирсона (С).

3. Общие принципы интерпретации коэффициентов корреляции.