Пусть плоскость 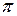 задана уравнением (4.6), а точка
задана уравнением (4.6), а точка 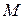 пространства своим радиус-вектором
пространства своим радиус-вектором 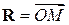 . Расстояние
. Расстояние 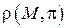 от точки
от точки 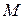 до плоскости
до плоскости 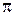 равно высоте параллелепипеда, построенного на векторах
равно высоте параллелепипеда, построенного на векторах 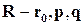 (рис. 9).
(рис. 9).
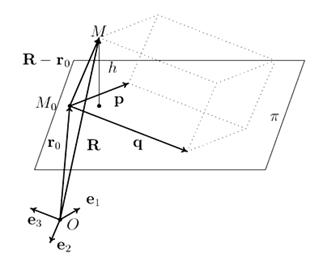
Рис. 9. Расстояние от точки до плоскости
Объем параллелепипеда равен модулю смешанного произведения этих векторов, а площадь его основания равна модулю векторного произведения 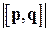 . Отсюда
. Отсюда
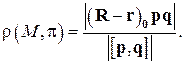 (4.11)
(4.11)
Для каждого вектора 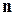 , нормального к плоскости, можно так выбрать направляющие векторы
, нормального к плоскости, можно так выбрать направляющие векторы 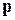 и
и 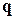 , чтобы
, чтобы 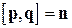 . Поэтому при любом нормальном векторе
. Поэтому при любом нормальном векторе 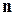 имеем
имеем
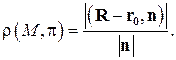 (4.12)
(4.12)
Пусть в прямоугольной декартовой системе координат
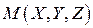 ,
, 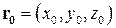 ,
, 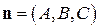 .
.
Тогда 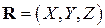 и (4.12) примет вид
и (4.12) примет вид
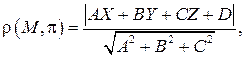 (4.13)
(4.13)
где 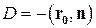 .
.
Рассмотрим в прямоугольной декартовой системе координат плоскость 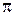 , заданную уравнением
, заданную уравнением
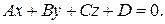 (4.14)
(4.14)
Пусть 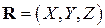 – радиус-вектор некоторой точки
– радиус-вектор некоторой точки 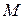 пространства,
пространства, 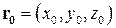 – радиус-вектор точки
– радиус-вектор точки 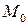 , являющейся проекцией точки
, являющейся проекцией точки 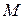 на плоскость
на плоскость 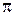 . Так как точка
. Так как точка 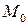 принадлежит плоскости
принадлежит плоскости 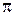 , ее координаты удовлетворяют уравнению (4.14), т. е.
, ее координаты удовлетворяют уравнению (4.14), т. е.
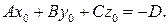 (4.15)
(4.15)
Вектор 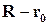 параллелен нормальному вектору
параллелен нормальному вектору 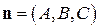 . Тогда
. Тогда
|
|
|
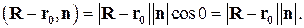
Отсюда
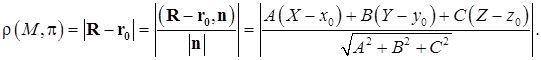
Используя (4.15), получим
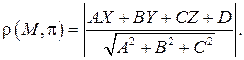 (4.16)
(4.16)
Уравнение
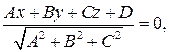
получаемое из (4.14) делением на 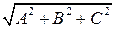 , называют нормированным уравнением плоскости. Его удобно использовать для нахождения расстояния от точки
, называют нормированным уравнением плоскости. Его удобно использовать для нахождения расстояния от точки 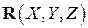 до плоскости. Достаточно найти модуль левой части этого уравнения при подстановке
до плоскости. Достаточно найти модуль левой части этого уравнения при подстановке 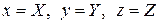 .
.
 2015-06-28
2015-06-28 435
435








