142. Доказать, что прямая, проведенная через середину одного основания равнобедренной трапеции перпендикулярно ему, делит пополам и второе основание.
143. Доказать, что если отрезок, соединяющий середины оснований трапеции, перпендикулярен этим основаниям, то трапеция равнобедренная.
144. Доказать, что если средние линии четырехугольника являются его осями симметрии, то такой четырехугольник является прямоугольником.
145. Доказать, что если одна диагональ и одна средняя линия четырехугольника являются его осями симметрии, то такой четырехугольник – квадрат.
146. Некоторая окружность пересекает одну из двух концентрических окружностей в точках 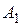 и
и 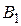 , а другую
, а другую 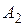 и
и 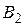 . Доказать, что хорды
. Доказать, что хорды 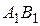 и
и 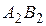 параллельны.
параллельны.
147. Окружность, концентрическая вписанной в треугольник 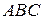 окружности, пересекает стороны
окружности, пересекает стороны 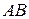 и
и 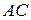 треугольника в точках
треугольника в точках 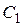 и
и 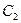 ,
, 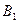 и
и 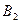 соответственно. Доказать, что хорды
соответственно. Доказать, что хорды 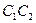 и
и  конгруэнтны.
конгруэнтны.
148. Окружность с центром на биссектрисе угла встречает стороны этого угла в точках 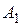 и
и 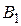 ,
, 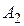 и
и 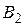 . Доказать, что хорды
. Доказать, что хорды 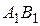 и
и 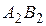 конгруэнтны.
конгруэнтны.
|
|
|
149. На одной стороне угла с вершиной 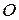 взяты точки
взяты точки 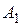 и
и 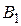 , а на другой стороне – точки
, а на другой стороне – точки 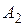 и
и 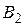 , так, что
, так, что 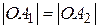 и
и 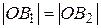 . Доказать, что отрезки
. Доказать, что отрезки 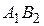 и
и 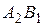 конгруэнтны и пересекаются на биссектрисе данного угла.
конгруэнтны и пересекаются на биссектрисе данного угла.
150. Пусть 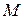 и
и 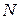 - середины оснований
- середины оснований 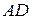 и
и 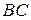 равнобедренной трапеции
равнобедренной трапеции 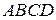 . Доказать, что: 1) центры
. Доказать, что: 1) центры 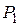 и
и 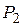 окружностей, вписанных в треугольники
окружностей, вписанных в треугольники 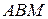 и
и 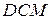 , равноудалены от точки
, равноудалены от точки 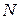 ; 2) центры
; 2) центры 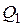 и
и  окружностей, описанных около треугольников
окружностей, описанных около треугольников 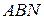 и
и 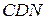 , равноудалены от точки
, равноудалены от точки 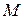 .
.
151. На равных сторонах 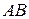 и
и 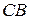 равнобедренного треугольника
равнобедренного треугольника 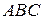 вне его построены квадраты с центрами
вне его построены квадраты с центрами 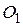 и
и 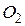 . Доказать, что: 1) пары прямых
. Доказать, что: 1) пары прямых 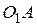 и
и 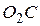 ,
, 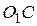 и
и 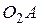 пересекаются на биссектрисе угла
пересекаются на биссектрисе угла 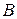 треугольника; 2) прямая
треугольника; 2) прямая 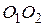 перпендикулярна биссектрисе угла
перпендикулярна биссектрисе угла 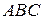 ; 3) отрезки
; 3) отрезки 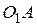 и
и 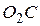 конгруэнтны; 4) отрезки
конгруэнтны; 4) отрезки 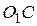 и
и 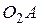 конгруэнтны.
конгруэнтны.
152. Даны две окружности 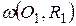 и
и 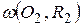 , пересекающиеся в точках
, пересекающиеся в точках  и
и  . Доказать, что угол, образованный касательными к этим окружностям в точке
. Доказать, что угол, образованный касательными к этим окружностям в точке  , равен углу между касательными к ним, проведенными в точке
, равен углу между касательными к ним, проведенными в точке 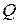 .
.
153. Доказать, что отрезок, соединяющий середины катетов прямоугольного треугольника, виден из основания высоты, проведенной к гипотенузе, под прямым углом.
154. Доказать, что из всех треугольников с данным основанием и высотой равнобедренный имеет наименьший периметр.
155. Высоты 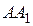 и
и 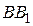 треугольника
треугольника 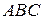 пересекают описанную около него окружность в точках
пересекают описанную около него окружность в точках 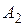 и
и 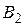 соответственно. Доказать, что точка, симметричная точке
соответственно. Доказать, что точка, симметричная точке 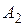 относительно прямой
относительно прямой 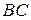 , совпадает с точкой, симметричной точке
, совпадает с точкой, симметричной точке 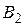 относительно прямой
относительно прямой 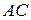 .
.
156. Доказать, что для произвольного треугольника 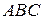 точки
точки 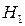 ,
, 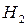 и
и 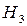 , симметричные ортоцентру
, симметричные ортоцентру 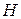 данного треугольника относительно его сторон, лежат на окружности, описанной около треугольника
данного треугольника относительно его сторон, лежат на окружности, описанной около треугольника 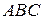 .
.
|
|
|
 2015-06-28
2015-06-28 1074
1074








