Определение. Уравнения, в которых неизвестные величины выражаются целыми числами, называются диофантовыми по имени математика Диофанта.
Рассмотрим уравнение
ах + bу = с (а 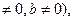 (1)
(1)
коэффициенты, которого а, b и с – целые числа.
Пусть d = D (а; b) или d = (а; b) или d = НОD (а; b) - наибольший общий делитель а и b.
Правило 1. Если с не делится на наибольший общий делитель (а; b), то уравнение (1) не имеет решений в целых числах (тем более в натуральных).
Правило 2. Если с 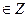 делится на НОD (а; b), то уравнение (1) имеет целые решения.
делится на НОD (а; b), то уравнение (1) имеет целые решения.
Если с 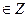 делится на НОD (а; b), то уравнение (1) следует упростить, разделив обе его части на НОD (а; b).
делится на НОD (а; b), то уравнение (1) следует упростить, разделив обе его части на НОD (а; b).
Правило 3. Если а и b –взаимно простые числа, то уравнение ах + bу = 1 имеет решение в целых числах х и у.
Правило 4. Чтобы найти решение уравнения (1) при взаимно простых а и b, нужно сначала найти решение (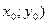 уравнения ах + bу = 1; числа
уравнения ах + bу = 1; числа 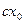 и
и 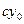 составят решение
составят решение
уравнения (1).
Правило 5. Если коэффициенты а и b уравнения (1) взаимно просты, то все решения уравнения (1) получаются по формулам х = 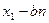 , у =
, у = 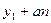 , n
, n 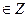 , где
, где 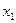 и
и  одно из решений этого уравнения.
одно из решений этого уравнения.
|
|
|
Пример 1. Решите диофантово уравнение 6 х + 9 у = 2.
Решение: НОD (6; 9) = 3, а 2 на 3 не делится. Значит, данное уравнение не имеет решений в целых числах.
Ответ: нет решений.
Пример 2. Решите в целых числах уравнение 28 х – 40 у = 60.
Решение: НОD (28; 40) = 4, число 60 делится на 4. Значит, уравнение имеет решений в целых числах. Сократим уравнение на 4, получим уравнение 7 х – 10 у = 15. Сначала подберём частное решение уравнения 7 х – 10 у = 1. НОD (7; 10) = 1. 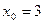 и
и 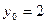 - частное решение уравнения 7 х – 10 у = 1.
- частное решение уравнения 7 х – 10 у = 1. 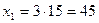 и
и 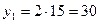 - частное решение уравнения 7 х – 10 у = 15.
- частное решение уравнения 7 х – 10 у = 15.
Общее решение уравнения 7 х – 10 у = 15 задаётся формулами
х = 45 + 10 t, у = 30 + 7 t, t 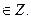
Ответ: (45 + 10 t, 30 + 7 t), t 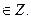
Пример 3. Решите диофантово уравнение 6 х +9 у = 3. (*)
Решение: НОD (6; 9) = 3, число 3 делится на 3. Значит, уравнение имеет решений в целых числах. Сократим уравнение на 3, получим уравнение 2 х + 3 у = 1.(1) Сначала подберём частное решение уравнения 2 х + 3 у = 1. х = 5, у = -3 является частным решением уравнения (1), так как справедливо равенство 2·5 + +3·(-3) = 1.
В уравнении (1) заменим число 1 выражением 2·5 + 3·(-3)
и преобразуем полученное уравнение:
2 х + 3 у = 2·5 + 3· (-3),
2 (х – 5) + 3 (у + 3) = 0. (2)
Введём новые неизвестные:
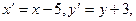 (3)
(3)
уравнение (2) перепишем в виде
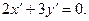 (4)
(4)
Все решения однородного уравнения (3) задаются формулами 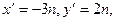 где n – любое целое число. Используя равенства (3), получим, что все решения уравнения (*) задаются формулами
где n – любое целое число. Используя равенства (3), получим, что все решения уравнения (*) задаются формулами 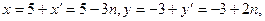 где n
где n 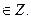
Ответ: (5 – 3 n, -3 + 2 n), n 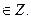
Линейные диофантовы уравнения применяются при решении задач.
Задача 1. У покупателя и продавца имеются монеты только по
2 р. и 5 р. Сможет ли покупатель заплатить за покупку
стоимостью 1 р.?
Решение: Если покупатель даст х монет по 2 р. и у монет по 5 р., то он заплатит (2 х + 5 у) р., или 1 р.
|
|
|
Следовательно, 2 х + 5 у = 1. (1)
Пара (3; -1) является частным решением уравнения (1), так как 2 · 3 + 5 · (-1) = 1. Это означает, что покупатель может дать 3 монеты по 2 р. и получить сдачу 1 монету по 5р.
Общее решение диофантова уравнения (1) имеет вид
х = 3 – 5 n, у = -1 + 2 n, где n 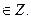
Способов оплаты товара стоимостью 1 р. в задаче 1 бесконечно много. Если, например, у окажется отрицательным, то это означает, что покупатель должен получить сдачу монетами по 5 р.
Ответ: Сможет.
 2015-06-28
2015-06-28 1016
1016








