Уравнение теплопроводности Фурье

Полученное ранее выражение теплового потока справедливо для стационарного одномерного температурного поля. В общем случае, как указывалось, температура в любой точке тела является функцией трех координат. Кроме того, она может меняться и во времени. Протекание теплового процесса в любой точке тела в любой момент времени описывается дифференциальный уравнением Фурье, которое является основным уравнением теплопро-

водности. Решение этого уравнения позволяет определить температуру в любой точке тела в любой момент времени.

Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Выделим в исследуемом теле элементарный параллелепипед объемом dv с ребрами dx, dy, dz (рис.3.2). Будем считать, что в пределах выделенного объема тело однородно (С и r постоянны) и изотропно (l по координатным осям одинаковы). Кроме того примем, что коэффициенты теплопроводности не зависят от температуры.

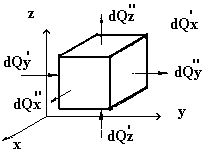
Рис.3.2. К выводу дифференциального уравнения

теплопроводности Фурье.

Для общности рассуждения положим, что тело имеет внутренние источники тепла, равномерно распределенные по объему.

Количество тепла dQ₁, введенное за время dt в элемент объема через его грани, и количество тепла dQ₂, выделяемое за это же время внутренними источниками тепла изменяют его внутреннюю энергию на величину

dQ = dQ₁ + dQ₂. (3.8)

Изменение внутренней тепловой энергии тела пропорционально его температуре

dQ = С r dv dt. (3.9)

где С - удельная теплоемкость, [Дж / кг ^о С],

r - плотность, [кг / м ³ ].

Подсчитаем приток тепла через грани элемента за время dt. Количество тепла dQ_x, притекающего по направлению оси x через грань dy, dz равно

dQ’_x = q_x dy dz dt.

Количество тепла dQ”_x, утекающего из объема по направлению оси x будет равно

dQ”_x = q_x+dx dy dz dt.

Приращение тепловой энергии в объеме за счет разности притока и стока равно

dQ_x = dQ’_x - dQ”_x = (q_x -q_x+dx) dy dz dt.

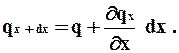Приращение dx мало, поэтому

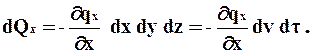Следовательно,

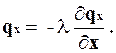Но плотность теплового потока, согласно закону Фурье, рав-

на

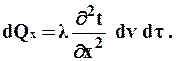Подставляя значение q_x в предыдущее выражение, получим

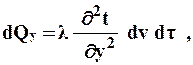Аналогично рассуждая, по другим координатным осям будем иметь

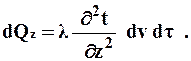Полное же количество тепла, переданное в объем через

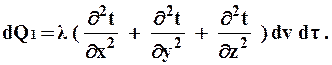грани, равно

Количество тепла dQ₂, выделяемое в объеме dv внутренними источниками тепла, будет

dQ₂ = W dv dt,

где W – удельная мощность источников тепла, [Вт/м ³ ].

Суммарное приращение количества тепла в объеме dv за время dt в соответствии с (2.8) будет равно

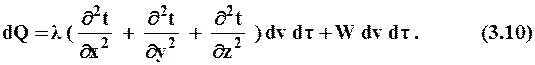Приравнивая правые части выражений (3.9) и (3.10), получим

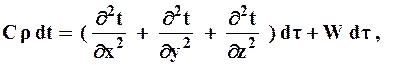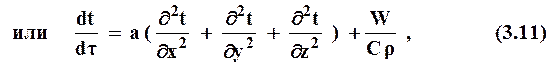где а = λ /С r -коэффициент температуропроводности,

характеризующий скорость изменения температуры в

теле.

Выражение (3.11) есть уравнение теплопроводности Фурье. Когда температура точек тела не меняется, dt/dt = 0 (поле стационарное), получим

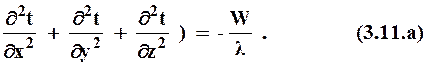Для анизотропных тел, у которых коэффициенты теплопроводности λ_x, λ_y, λ_z различны по координатным осям, уравнение Фурье имеет вид

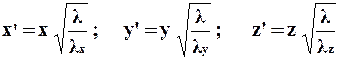Это уравнение путем преобразования системы координат в виде

λ_x, λ_y, λ_z

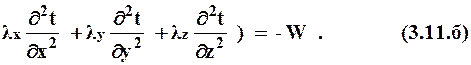приводится к уравнению, аналогичному для изотропного тела (3.11), где вместо x, y, z подставляются преобразованные координаты x’, y’, z’

При преобразовании координат через λ обозначается некоторая базовая теплопроводность, выбор которой произволен. Обычно за λ принимается одно из значений теплопроводности λ_x, λ_y, λ_z.

Для решения дифференциального уравнения необходимо иметь начальные и граничные условия, соответственно характеризующие начальное распределение температуры в теле и особенности протекания процесса теплообмена поверхности тела с окружающей средой.