Определение. Двумерная случайная величина  называется дискретной, если случайные величины Х и Y дискретны.
называется дискретной, если случайные величины Х и Y дискретны.
Если случайная величина Х может принимать только значения 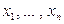 (для простоты изложения ограничимся только конечным множеством значений), а случайная величина Y – значения
(для простоты изложения ограничимся только конечным множеством значений), а случайная величина Y – значения 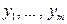 , то двумерный случайный вектор
, то двумерный случайный вектор  может принимать только пары значений
может принимать только пары значений 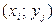 , где
, где 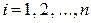 ,
, 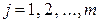 . Также, как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описывается с помощью таблицы:
. Также, как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описывается с помощью таблицы:
| Y X | 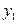
| 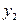
| … | 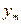
| 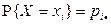
|
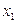
| 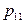
| 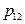
| … | 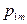
| 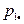
|
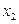
| 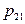
| 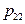
| … | 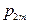
| 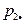
|
| … | … | … | … | … | … |
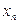
| 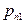
| 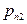
| … | 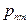
| 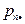
|
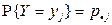
| 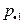
| 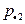
| … | 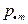
| |
В этой таблице 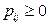 и
и 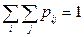 .
.
Одномерные законы распределения отдельных компонент случайного вектора  выражаются через вероятности совместных значений
выражаются через вероятности совместных значений 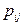 по формулам:
по формулам:
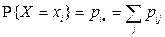 ,
, 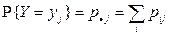 ,
,
где суммирование распространяется на все возможные значения индексов i или j. Уточним, что для получения значения вероятности 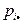 для некоторого фиксированного значения i, надо сложить вероятности
для некоторого фиксированного значения i, надо сложить вероятности 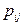 , стоящие в i -ой строке таблицы, а для получения значения вероятности
, стоящие в i -ой строке таблицы, а для получения значения вероятности 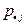 для некоторого фиксированного значения j, надо сложить вероятности
для некоторого фиксированного значения j, надо сложить вероятности 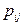 , стоящие в j -ом столбце таблицы. При этом удобно одномерные законы распределения отдельных компонент записывать в той же таблице (см. ее последнюю строку и последний столбец). В правом нижнем углу таблицы обязательно должна находиться единица, являющаяся результатом суммирования вероятностей в ее последней строке (последнем столбце) и соответствующая условию нормировки. С помощью таблицы нетрудно определить функцию распределения
, стоящие в j -ом столбце таблицы. При этом удобно одномерные законы распределения отдельных компонент записывать в той же таблице (см. ее последнюю строку и последний столбец). В правом нижнем углу таблицы обязательно должна находиться единица, являющаяся результатом суммирования вероятностей в ее последней строке (последнем столбце) и соответствующая условию нормировки. С помощью таблицы нетрудно определить функцию распределения
|
|
|
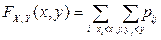 .
.
Также легко по таблице вычисляется вероятность любого события B, задаваемого в виде произвольной области на плоскости:
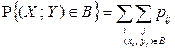 .
.
Пример 2.2.4. Закон распределения двумерного дискретного случайного вектора  задан таблицей:
задан таблицей:
| Y X | –1 | |
| 0,1 | 0,06 | |
| 0,3 | 0,18 | |
| 0,2 | 0,16 |
Найти: одномерные законы распределения компонент X и Y; вероятность 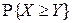 . Составить функцию распределения
. Составить функцию распределения 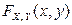 .
.
Решение. 1) Одномерные законы 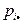 и
и 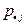 распределения компонент X и Y соответственно построены в таблице:
распределения компонент X и Y соответственно построены в таблице:
| Y X | –1 | 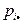
| |
| 0,1 | 0,06 | 0,16 | |
| 0,3 | 0,18 | 0,48 | |
| 0,2 | 0,16 | 0,36 | |
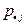
| 0,6 | 0,4 |
2) 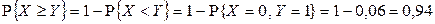 .
.
3) Согласно определению функции распределения 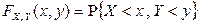 . Напомним, что геометрически значение
. Напомним, что геометрически значение 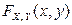 – это вероятность попадания случайной точки
– это вероятность попадания случайной точки  в бесконечный квадрант с вершиной
в бесконечный квадрант с вершиной 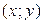 . Для вершины этого квадранта, согласно условию задачи, есть двенадцать областей, образованных тремя вертикальными прямыми
. Для вершины этого квадранта, согласно условию задачи, есть двенадцать областей, образованных тремя вертикальными прямыми 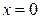 ,
,  ,
, 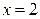 и двумя горизонтальными прямыми
и двумя горизонтальными прямыми 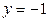 ,
, 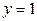 .
.
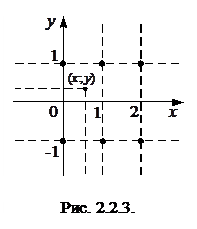 На рис. 2.2.3 показан случай, когда вершина
На рис. 2.2.3 показан случай, когда вершина 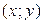 находится внутри прямоугольника
находится внутри прямоугольника 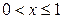 ,
, 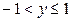 . При этом внутри квадранта находится только одна точка с координатами
. При этом внутри квадранта находится только одна точка с координатами 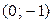 , в которой имеется ненулевая вероятность, равная 0,1. Функцию распределения
, в которой имеется ненулевая вероятность, равная 0,1. Функцию распределения 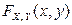 удобно задавать в виде таблицы (ее значение для случая, когда вершина
удобно задавать в виде таблицы (ее значение для случая, когда вершина 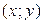 квадранта находится внутри прямоугольника
квадранта находится внутри прямоугольника 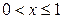 ,
, 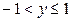 выделено жирным шрифтом):
выделено жирным шрифтом):
|
|
|
| y x | 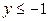
| 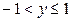
| 
|
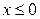
| |||
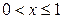
| 0,1 | 0,16 | |
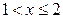
| 0,4 | 0,64 | |
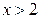
| 0,6 |
Пример 2.2.5. Известна функция распределения 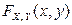 двумерного дискретного случайного вектора
двумерного дискретного случайного вектора  :
:
| y x | 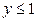
| 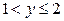
| 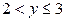
| 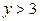
|
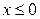
| ||||
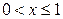
| 0,5 | 0,5 | 0,5 | |
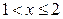
| 0,5 | 0,75 | 0,75 | |
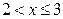
| 0,5 | 0,75 | 0,875 | |
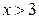
| 0,5 | 0,75 |
Составить функции распределения 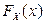 и
и 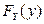 компонент X и Y, а затем построить их законы распределения.
компонент X и Y, а затем построить их законы распределения.
Решение. Учитывая, что 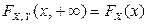 ,
, 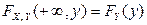 , получим («проходя» соответственно по последнему столбцу и последней строке таблицы):
, получим («проходя» соответственно по последнему столбцу и последней строке таблицы):
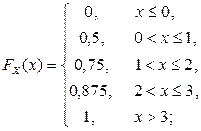

Значит, для случайной величины X функция распределения испытывает «скачки» в точках 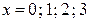 , для случайной величины Y – в точках
, для случайной величины Y – в точках 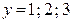 . Поэтому законы распределения компонент выглядят следующим образом:
. Поэтому законы распределения компонент выглядят следующим образом:
| X | Y | ||||||||
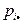
| 0,5 | 0,25 | 0,125 | 0,125 | 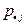
| 0,5 | 0,25 | 0,25 |
 2015-06-28
2015-06-28 1551
1551








