Совместное применение главных принципов к идеальному ансору

Изучение различных качественных и количественных свойств ансаты целесообразно начать с рассмотрения уравнений состояния идеального ансора. При этом максимально упрощается математический аппарат исследования и, кроме того, удается установить много принципиально важных для всего последующего понятий, которые также представляют собой предельные абстракции.

Очевидно, что от полной совокупности уравнений состояния остаются только уравнения первого (закон энергии) и второго (закон состояния) порядков. Например, при n = 2 интегрирование дифференциального уравнения состояния (26) второго порядка для идеального тела (А = const) дает

Р₁ = А₁₁Е₁ + А₁₂Е₂; (250)

Р₂ = А₂₁Е₁ + А₂₂Е₂, (250)

где

А₁₂ = А₂₁.

При n степенях свободы из уравнения (29) после интегрирования получаем

Р_i = 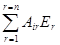, (251)

где i = 1, 2,..., n;

А_ir = А_ri.

Из формул (32) и (43) для n = 1 имеем

Р = АЕ; Е = КР. (252)

Из уравнений (250) и (251) видно, что каждый интенсиал является функцией всех полных экстенсоров тела. При этом сохраняют силу равенства (51) и (52), характеризующие симметрию во взаимном влиянии степеней свободы. Из формул (252) следует, что при n = 1 у идеального ансора интенсиал пропорционален экстенсору. Например, температура пропорциональна термиору, квадрат скорости – массе, механиал – плотности, электрический потенциал – электрическому заряду, сила – деформации (закон Гука), момент силы – углу закручивания и т.д.

Найденные уравнения состояния идеального ансора позволяют легко проинтегрировать уравнения первого порядка закона энергии. Например, для n = 2 из выражений (3) и (250) находим

dU = A₁₁E₁dE₁ + A₂₂E₂dE₂ + A₁₂E₂dE₁ + A₂₁E₁dE₂ дж

Применение соотношения взаимности (51) четвертого закона позволяет переписать это уравнение в виде

dU = A₁₁E₁dE₁ + A₂₂E₂dE₂ + A₁₂d(E₁E₂) дж;

После интегрирования имеем

U = (1/2)A₁₁E²₁ + (1/2)A₂₂E²₂ + A₁₂E₁Е₂ дж; (253)

U = (1/2)Р₁E₁ + (1/2)Р₂E₂ дж; (254)

U = [(1/2)A₂₂Р²₁ + (1/2)A₁₁Р²₂ - A₁₂Р₁Р₂]/(А₁₁А₂₂ – А²₁₂) дж; (255)

Как видим, энергия идеального ансора зависит не только от основных коэффициентов, но и от перекрестных, которыми определяется взаимное влияние внутренних степеней свободы. Проще всего выглядят уравнения типа (254), выраженные через экстенсоры и интенсиалы одновременно. В этих уравнениях взаимное влияние степеней свободы завуалировано. Аналогичную форму имеют уравнения, определяющие энергию идеального ансора при большем числе степеней свободы.

Например, при n степенях свободы уравнение типа (254) приобретает вид

U = 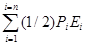дж. (256)

Оно получается путем совместного интегрирования выражений(5) и (251).

В гипотетическом случае одной степени свободы находим

U = (1/2)АЕ² = (1/2)РЕ= (1/2)КР² дж. (257)

Именно в таком виде в физике определяется энергия применительно к различным степеням свободы. Например, так находится кинетическая энергия движущегося тела (формулы (205) и (225)), энергия сжатого или растянутого упругого тела и т.д. Исключение составляет лишь термическая элата, для которой обычно принимается, что энергия пропорциональна температуре в первой степени. В общей теории для термиаты исключение не делается. Энергия термиаты определяется по следующей формуле, являющимся частным случаем общего выражения (257):

U = (1/2)А_QQ² = (1/2)ТQ = (1/2)К_QТ² дж. (258)

Энергия идеального ансора в условиях одной степени свободы пропорциональна температуре в квадрате.

Интересно отметить, что равенство (253) выражает энергию ансора только через экстенсоры, равенство (254) – через экстенсоры и интенсиалы одновременно, равенство (255) – только через интенсиалы. Наибольший интерес представляют уравнения (254) и (256), так как не содержат физических коэффициентов. Каждое слагаемое уравнения (256)

U_i = (1/2)Р_iЕ_i (259)

соответствует определенной частной составляющей полной энергии ансора. В виде суммы таких составляющих U_i представлена энергия ансора в формуле (1). Равенство (259) определяет значения величин U_i для идеального ансора.

Если подвод или отвод экстенсора происходит не постепенно, а скачкообразно, тогда множители (1/2) в уравнении (256) пропадают. Имеем

U = 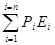дж. (260)

Например, так приходится записывать уравнение энергии для отдельных экстенсоров.

Возможность представить уравнение энергии ансора в виде равенств (256) и (260) объясняет причину того, что в термодинамике широко и с большим успехом применяются так называемые характеристические функции, или термодинамические потенциалы. В частности, известная формула (165) превращается в уравнение (260), если положить r = n и А = 0. Таким образом, никакой принципиальной разницы между уравнениями (256) и (260), справедливыми для идеального ансора, не существует.

Из найденных общих соотношений для идеального ансора могут быть получены многие частные формула, удобные для практических расчетов. Например, если ансор располагает двумя степенями свободы, из которых одна термическая, тогда уравнения (250) дают

Т = А_QQQ + А_QЕЕ; (261)

Р = А_ЕQQ + А_ЕЕЕ; (261)

где

А_ЕQ = А_QЕ.

Здесь первая строчка относится к термической элате, а вторая – к любой другой – механической, деформационной, электрической, магнитной и т.д. В частности, для термомеханического ансора из уравнений (261) получаем

Т = А_QQQ + А_QVV; (262)

p = А_VQQ + А_VVV; (262)

где

А_QV = - А_VQ.

Здесь величины А_VV и А_QV отрицательны, так как приращение давления и объема в соответствующих производных имеют различные знаки. Уравнения состояния (262) описывают свойства особого идеального газа, который рассматривается в общей теории. Особенностью уравнений (262) служит то, что они в качестве равноправного параметра включают в себя термиор. При этом температура системы является линейной функцией термиора. В этом заключается главное отличие особого идеального газа от обычного, определяемого известным уравнением Клапейрона.

Общие уравнения (261) приводят еще к одному очень интересному частному уравнению, которое выводится в работах [10, 14]. Имеем

Р = ЕRТ, (263)

где R - коэффициент пропорциональности.

Из этого выражения при Р º р и Е º r вытекает уравнение состояния обычного идеального газа Клапейрона, объединяющее в себе газовые законы Шарля, Гей-Люссака и Бойля – Мариотта. Коэффициент R представляет собой газовую постоянную.

Для термоосмотической системы из уравнения (263) при Р º р и Е º С (концентрация раствора, кг/м³) получается известная формула закона Вает-Гоффа.

В электронной теории электропроводности Друде и Лоренца с помощью уравнения типа (263) определяется давление электронного газа в металлах. Уравнение типа (263) применяется также для описания термодеформационной (с помощью законов Дюлонга и Пти и Неймана и Коппа), термополяризационной, термомагнитной (с помощью закона Кюри – Вейса) и других систем [14].

А работах [11] и [14] приводятся экспериментальные данные, подтверждающие тот факт, что в реальных условиях общий характер зависимостей интенсиалов от экстенсоров отвечает приведенным выше уравнениям для идеального ансора. Кроме того, там имеются экспериментальные данные, подтверждающие закон взаимности.