2015-06-28
403Типовой расчет «теория вероятности и математическая статистика»
Вариант 1
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,9, n = 4, m = 2. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков равна 7, а разность равна 2.
c)В ящике 11 деталей, из которых 3 нестандартных. Наугад извлекают 3 детали. Найти вероятность того, что они стандартные.
d)В круг радиуса R =17 помещен правильный шестиугольник со стороной, равной 8. Найти вероятность того, что точка окажется внутри шестиугольника. Предполагается, что вероятность попадания точки в шестиугольник пропорциональна площади шестиугольника и не зависит от его расположения относительно круга.
e)Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,85, второй – 0,6. Найти вероятность того, что при аварии сработает только первый сигнализатор.
|
|
|
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,9 и x 2, причем х 1 < х 2, М (X)=3,1 и D(X)=0,09.
3. Случайная величина Х задана функцией распределения
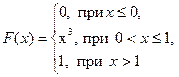
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α = 0,5, β = 0,8. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности:
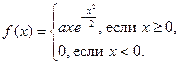
Найти: а) коэффициент а; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 2, β = 14, m = 9, σ = 5, δ = 7.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 0,455 | 0,459 | 0,240 | 0,565 | 0,214 |
| 0,214 | 0,260 | 0,531 | 0,552 | 0,477 |
| 0,020 | 0,580 | 0,486 | 0,461 | – 0,019 |
| 0,806 | 0,662 | 0,276 | 0,467 | 0,571 |
| 0,574 | 0,437 | 0,305 | 0,581 | 0,782 |
| 0,603 | 0,769 | 0,136 | 0,720 | – 0,016 |
| 0,397 | 0,764 | 0,728 | 0,503 | – 0,130 |
| 0,050 | 0,726 | 0,389 | 0,167 | 0,967 |
| 0,485 | 0,665 | 0,677 | 0,487 | 0,023 |
| 0,484 | 0,373 | 0,456 | 0,315 | 0,731 |
7. Найти выборочное уравнение прямой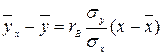 
регрессии y на x по данным корреляционной табл. 1.
Таблица 1
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 2
|
|
|
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,8, n = 4, m = 3. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков равна 8, а разность – 4.
c)Студент знает 13 из 20 экзаменационных вопросов. Ему предлагают ответить на 2 вопроса. Какова вероятность того, что он знает ответ на оба вопроса?
d)В круг радиуса R =9 помещен правильный шестиугольник со стороной, равной 5. Найти вероятность того, что точка окажется внутри шестиугольника. Предполагается, что вероятность попадания точки в шестиугольник пропорциональна площади шестиугольника и не зависит от его расположения относительно круга.
e) Вероятность попадания в цель при одном залпе для первого орудия равна 0,85, а для второго орудия – 0,95. Найти вероятность того, что при одном залпе в цель попадет только одно из орудий.
2. Найти закон распределения случайной величины Χ, которая принимает только два возможных значения: х 1 с известной вероятностью р 1 = 0,8 и х 2, причeм х 1 < х 2, М (Х) = 3,2 и D (X) = 0,16.
3. Случайная величина Х задана функцией распределения
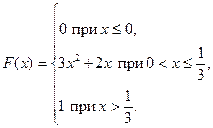
Найти: а) плотность вероятности f (x); б) M (X); в) D (X); г) σ (X); д) P (α < x < β), α = 0,1, β = 0,2. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
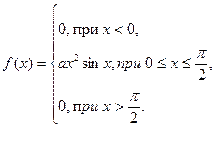
Найти: а) коэффициент a; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 5, β = 14, m = 10, σ = 4, δ = 6.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (Х)и σ 2(Х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 0,255 | 0,786 | 0,819 | 0,536 | 0,427 |
| 0,353 | 0,467 | 0,594 | 0,165 | 0,269 |
| 0,576 | 1,138 | 0,362 | 0,413 | 0,789 |
| 0,735 | 0,800 | 0,732 | 0,280 | 0,972 |
| – 0,004 | 0,230 | 0,360 | 0,447 | 0,707 |
| 0,344 | 0,419 | 0,691 | 1,006 | 0,355 |
| 1,124 | 0,061 | 0,601 | 0,490 | 0,772 |
| 0,443 | 0,255 | 0,293 | 0,636 | 0,396 |
| 0,183 | 0,567 | 0,557 | 0,360 | 0,469 |
| 0,299 | 0,647 | 0,454 | 0,379 | 0,431 |
7. Найти выборочное уравнение прямой 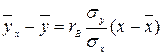регрессии y на x по данным корреляционной табл. 2.
Таблица 2
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 3
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,7, n = 5, m = 2. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b) Для новогодней лотереи отпечатали 150 билетов, из которых 70 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
c)В наборе 7 белых и 16 черных шаров. Наугад извлекают два шара. Найти вероятность того, что только один шар черный.
d)В круг радиуса R =12 помещен правильный треугольник с высотой, равной 6. Найти вероятность того, что точка окажется внутри треугольника. Предполагается, что вероятность попадания точки в треугольник пропорциональна площади треугольника и не зависит от его расположения относительно круга.
e)Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна – 0,7, а для второго – 0,8. Найти вероятность того, при одном залпе в мишень попадет только один из стрелков.
|
|
|
2. Найти закон распределения случайной величины Χ, которая принимает только два возможных значения: х 1 с известной вероятностью р 1 = 0,7 и х 2, причeм х 1 < х 2, М (Х) = 3,3 и D (X) = 0,21.
3. Случайная величина Х задана функцией распределения
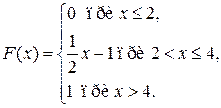
Найти: а) плотность вероятности f (x); б) M (X); в) D (X); г) σ (X); д) P (α < x < β), α = 2,5, β = 3; е) построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
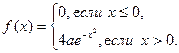
Найти: а) коэффициент a; б) F (x); в) построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 4, β = 9, m = 8, σ = 1, δ = 2.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (Х)и σ 2(Х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| –0,517 | 0,465 | 0,568 | 0,217 | 0,212 |
| –0,639 | 0,743 | 0,826 | 1,049 | 0,459 |
| 0,068 | –0,454 | 1,616 | 1,398 | 1,729 |
| 0,311 | 0,617 | 0,915 | 1,191 | 0,379 |
| 0,521 | 0,214 | 0,554 | 2,440 | –0,840 |
| 1,146 | 0,475 | 0,966 | 0,168 | –0,591 |
| 0,627 | 1,133 | 0,281 | 2,635 | 0,411 |
| 0,111 | 0,460 | –0,494 | 0,460 | 1,201 |
| 0,294 | 0,448 | 0,822 | 1,310 | 0,372 |
| –0,279 | 0,545 | 2,376 | 0,002 | 0,499 |
7. Найти выборочное уравнение прямой 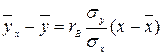регрессии y на x по данным корреляционной табл. 3.
Таблица 3
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 4
1. a)Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз, если известно, что в каждом испытании вероятность появления события равна р = 0,6, n = 5, m = 3.
b) Какова вероятность того, что при бросании игрального кубика выпадет: а) 1 очко; б) более 3 очков?
|
|
|
c)Устройство состоит из пяти элементов, из которых два изношены. При включении устройства должны включаться два элемента. Найти вероятность того, что включенные элементы – изношенные.
d)Внутрь круга радиуса R брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата.
e)В группе 21 студент, в том числе 5 отличников, 10 хорошо занимающихся, 6 занимающихся слабо. На предстоящем экзамене отличники могут получить только отличные оценки, хорошо занимающиеся студенты – отличные и хорошие оценки, слабо занимающиеся студенты, могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена наугад приглашается один студент. Найти вероятность того, что он получит хорошую или отличную оценку.
2. Найти закон распределения случайной величины Χ, которая принимает только два возможных значения: х 1 с известной вероятностью р 1 = 0,6 и х 2, причем х 1 < х 2, М (Х) = 3,4 и D (X) = 0,24.
3. Случайная величина Х задана функцией распределения
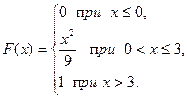
Найти: а) плотность вероятности f (x); б) M (X); в) D (X); г) σ (X); д) P (α < x < β), α = 1, β = 2,8. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
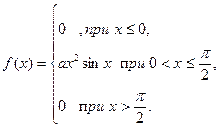
Найти: а) коэффициент a; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 3, β = 10, m = 7, σ = 2, δ = 4.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (Х)и σ 2(Х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 1,252 | – 0,710 | – 0,040 | 1,048 | – 0,032 |
| – 1,287 | 0,275 | 1,142 | – 0,584 | – 1,495 |
| – 0,852 | 0,594 | 1,556 | – 0,163 | 0,346 |
| 0,161 | – 0,341 | 2,883 | 1,161 | 0,325 |
| 1,323 | 1,556 | – 1,822 | 0,017 | – 0,604 |
| 0,557 | 1,069 | 0,706 | 0,987 | 0,822 |
| 2,644 | – 0,385 | 1,975 | 0,333 | 1,628 |
| 1,700 | – 0,571 | – 0,886 | 1,437 | – 1,598 |
| – 0,305 | 1,471 | 0,427 | – 0,070 | 1,209 |
| 0,961 | 2,386 | 2,282 | – 0,551 | 1,230 |
7. Найти выборочное уравнение прямой 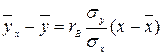регрессии y на x по данным корреляционной табл. 4.
Таблица 4
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 5
1. a)Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз, если известно, что в каждом испытании вероятность появления события равна р = 0,4; n = 4; m = 3.
b)Устройство состоит из пяти элементов, из которых два изношены. При включении устройства должны включаться два элемента. Найти вероятность того, что включенные элементы – неизношенные.
c)4 билета на ёлку распределили по жребию между 15 юношами и 12 девушками. Какова вероятность того, что билеты достанутся 2 юношам и 2 девушкам?
d)Внутрь круга радиуса R брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного треугольника.
e)Три стрелка делают по одному выстрелу в мишень. Вероятности попадания стрелками в мишень соответственно равны 0,8; 0,8; 0,9. Составить ряд распределения попаданий в мишень, построить многоугольник распределения. Найти функцию распределения и построить её график.
2. Найти закон распределения случайной величины Χ, которая принимает только два возможных значения: х 1 с известной вероятностью р 1 = 0,4 и х 2, причем х 1 < х 2, М (Х) = 3,6 и D (X) = 0,24.
3. Случайная величина Х задана функцией распределения
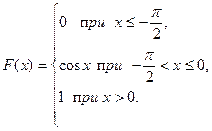
Найти: а) плотность вероятности f (x); б) M (X); в) D (X); г) σ (X); д) P (α < x < β), α =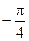 
, β = 0. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
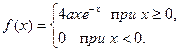
Найти: а) коэффициент a; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 1, β = 12, m = 5, σ = 1, δ = 5.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (Х)и σ 2(Х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 4,576 | 0,378 | 1,959 | 4,142 | 0,259 |
| 0,808 | – 0,734 | 3,124 | 1,596 | – 0,309 |
| 1,451 | 2,961 | – 0,207 | 1,927 | 7,558 |
| 4,904 | – 1,440 | 1,966 | 0,569 | – 0,186 |
| 0,443 | 0,717 | 3,871 | 0,976 | – 0,914 |
| 4,434 | 0,211 | 3,228 | 1,938 | 0,244 |
| 2,811 | 1,831 | 1,939 | – 1,668 | 2,233 |
| 1,876 | 1,865 | 1,008 | 0,966 | 5,369 |
| 1,885 | 1,438 | – 0,453 | 0,312 | 2,915 |
| 0,135 | 2,442 | 2,136 | 3,782 | – 0,937 |
7. Найти выборочное уравнение прямой 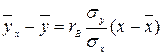регрессии y на x по данным корреляционной табл. 5.
Таблица 5
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 6
1. a)Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз, если известно, что в каждом испытании вероятность появления события равна р = 0,3; n = 5; m = 2.
b)В доме 120 квартир. Из них 12 находится на 1 этаже, 12 – на последнем. Какова вероятность того, что жильцу не достанется квартира, расположенная на первом или последнем этажах.
c)Студент знает 8 из 10 вопросов. Ему предлагают ответить на 3 вопроса. Какова вероятность того, что он знает ответ на все вопросы?
d)Внутрь круга радиуса R брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника.
e) В ящике 15 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает две детали. Найти вероятность того, что хотя бы одна деталь окажется окрашенной.
2. Найти закон распределения случайной величины Χ, которая принимает только два возможных значения: х 1 с известной вероятностью р 1 = 0,3 и х 2, причем х 1 < х 2, М (Х) = 3,7 и D (X) = 0,21.
3. Случайная величина Х задана функцией распределения
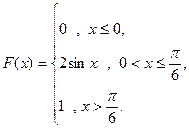
Найти: а) плотность вероятности f (x); б) M (X); в) D (X); г) σ (X); д) P (α < x < β), α = 0, β =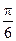 
. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
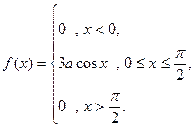
Найти: а) коэффициент a; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 2, β = 11, m = 4, σ = 5, δ = 6.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (Х)и σ 2(Х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| – 0,687 | 4,507 | 1,081 | – 0,734 | – 1,635 |
| 2,839 | 3,328 | 1,977 | 4,220 | 1,801 |
| 1,529 | 4,398 | – 1877 | 3,712 | 0,294 |
| – 0,573 | -0,640 | 0,543 | 2,061 | – 1,141 |
| 0,333 | 2,964 | 0,759 | 3,101 | – 2,212 |
| – 0,196 | 1,388 | 2,222 | 0,535 | 0,208 |
| 1,241 | – 2,028 | 1,642 | 0,624 | 4,655 |
| 4,583 | 5,888 | 4,824 | 2,604 | 0,043 |
| 1,992 | 0,751 | 1,333 | 2,818 | 2,441 |
| 3,507 | 4,293 | 1,110 | – 1,606 | 3,692 |
7. Найти выборочное уравнение прямой 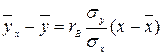регрессии y на x по данным корреляционной табл. 6.
Таблица 6
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 7
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,8, n = 4, m = 2. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)В ящике имеется 22 деталей, среди которых 17 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся неокрашенными.
c)Библиотечка состоит из 10 книг, причем 5 книг стоят по 400 рублей каждая, три – по 100 рублей, а две книги по 300 рублей. Найти вероятность того, что из 5 книг две окажутся стоимостью 400 рублей.
d)В правильный шестиугольник вписан круг радиуса r. Определить вероятность того, что взятая в шестиугольнике точка будет принадлежать кругу.
e)В вазе 37 гвоздик, из которых 21 красных. В темноте наугад вынимают 7 гвоздик. Какова вероятность того, что хотя бы одна из них будет красной?
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,9 и x 2, причем х 1 < х 2, М (X)=3,9 и D (X)=0,09.
3. Случайная величина Х задана функцией распределения
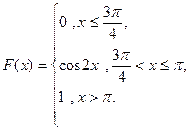
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α =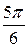 
0,5, β = π. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
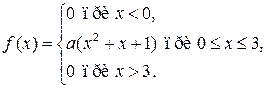
Найти: а) коэффициент а; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 4, β = 9, m = 2, σ = 5, δ = 8.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 3,967 | 3,940 | – 1,836 | – 2,157 | – 1,556 |
| 4,865 | 5,865 | 5,393 | 1,723 | – 2,330 |
| 1,261 | 2,404 | 0,972 | 0,080 | 2,142 |
| – 4,740 | 1,448 | 4,399 | 0,653 | 8,242 |
| 8,413 | – 2,600 | 3,737 | 0,479 | – 3,831 |
| 7,311 | 3,343 | 0,987 | 1,687 | 2,167 |
| 0,588 | – 0,098 | 6,183 | – 0,082 | 3,356 |
| 9,221 | – 5,210 | 3,229 | 0,076 | 4,350 |
| – 0,305 | 5,242 | 0,061 | 1,142 | 11,926 |
| 1,252 | 2,834 | 1,459 | 1,450 | – 2,317 |
7. Найти выборочное уравнение прямой 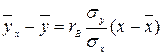регрессии y на x по данным корреляционной табл. 7.
Таблица 7
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 8
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,9, n = 4, m = 3. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)При бросании двух игральных кубиков два игрока поспорили: если в сумме выпадет число очков, кратное 5, то выигрывает первый игрок, если – 6, то выигрывает второй игрок. У кого из игроков больше шансов выиграть?
c)В коробке лежит 8 красных карандашей и 4 синих. Из коробки наугад вынимают 5 карандашей. Какова вероятность того, что 3 из них окажутся красными, а 2 синими?
d)В квадрат вписан круг радиуса r. Определить вероятность того, что взятая в квадрате точка будет принадлежать кругу.
e) Среди 150 лотерейных билетов есть 8 выигрышных. Найти вероятность того, что из двух наудачу выбранных билетов хотя бы один окажется выигрышным.
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,9 и x 2, причем х 1 < х 2, М (X)=2,2 и D (X)=0,36.
3. Случайная величина Х задана функцией распределения
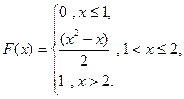
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α = 1,1, β = 1,9. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
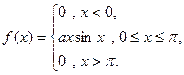
Найти: а) коэффициент а; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 6, β = 10, m = 2, σ = 4, δ = 9.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| – 2,975 | – 5,822 | 2,680 | – 3,001 | – 0,695 |
| 4,702 | 3,172 | – 3,660 | – 0,130 | 4,738 |
| – 0,924 | – 1,186 | 5,796 | 4,465 | – 1,173 |
| – 6,502 | – 1,519 | – 3,117 | 7,493 | – 4,625 |
| 9,576 | 1,991 | 6,318 | 1,060 | – 1,440 |
| – 4,953 | 0,655 | – 0,983 | 10,145 | 6,657 |
| 2,018 | 6,927 | – 3,402 | – 3,510 | 2,652 |
| 3,510 | 0,556 | 5,100 | 9,072 | 5,101 |
| 3,843 | 2,040 | 4,775 | 2,797 | – 3,226 |
| 5,694 | – 5,976 | – 2,321 | – 3,082 | 8,389 |
7. Найти выборочное уравнение прямой 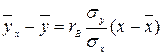регрессии y на x по данным корреляционной табл. 8.
Таблица 8
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 9
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,1, n = 4, m = 2. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)В ящике 80 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей все бракованные.
c) Студент знает 7 из 13 экзаменационных вопросов. Ему предлагают ответить на 2 вопроса. Какова вероятность того, что он знает ответ на один вопрос?
d). В правильный треугольник вписан круг радиуса r. Определить вероятность того, что взятая в треугольнике точка будет принадлежать кругу.
e)В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны извлекают по одному шару и кладут в мешок. Найти вероятность того, что наудачу вынутый из мешка шар окажется белым.
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,1 и x 2, причем х 1 < х 2, М (X) = 3,3 и D (X) = 0,25.
3. Случайная величина Х задана функцией распределения
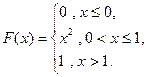
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α = 0,1, β = 0,9. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
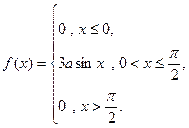
Найти: а) коэффициент а; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 16, β = 25, m = 15, σ = 2, δ = 4.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 2,838 | 6,202 | 1,867 | 5,969 | 7,090 |
| – 6,047 | 8,343 | 8,929 | – 3,720 | 2,424 |
| 9,688 | 5,862 | 0,457 | 3,880 | 0,840 |
| 1,154 | 6,800 | – 4,123 | 1,273 | – 0,115 |
| 3,300 | – 0,954 | – 1,648 | 5,227 | 5,846 |
| – 0,467 | – 0,321 | 6,744 | 0,306 | 1,016 |
| – 2,052 | – 7,561 | 0,692 | 2,457 | – 5,037 |
| 5,684 | 2,337 | – 6,605 | – 5,364 | 4,460 |
| 5,562 | 4,875 | 8,294 | 5,295 | 5,760 |
| 4,843 | 0,817 | 3,721 | 0,040 | 6,774 |
7. Найти выборочное уравнение прямой 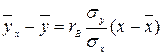регрессии y на x по данным корреляционной табл. 9.
Таблица 9
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 10
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,2, n = 4, m = 3. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)В ящике 150 деталей, из них 17 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных.
c)В коробке 19 одинаковых изделий, 13 из которых окрашено. Наудачу извлечены два изделия. Найти вероятность того, что одно изделие окажется окрашенным.
d)В круг радиуса R = 8 помещен квадрат, диагональ которого равна 6. Найти вероятность того, что точка окажется внутри квадрата. Предполагается, что вероятность попадания точки в квадрат пропорциональна площади квадрата и не зависит от его расположения относительно круга.
e)Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная – 0,8, второго – 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,2 и x 2, причем х 1 < х 2, М (X)=2,6 и D (X)=0,64.
3. Случайная величина Х задана функцией распределения
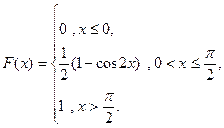
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α =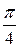 
, β =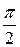 
. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
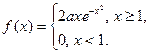
Найти: а) коэффициент а; б) F (x); в) построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 15, β = 17, m = 13, σ = 4, δ = 6.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| – 0,088 | 1,923 | 9,013 | – 8,985 | 8,095 |
| 10,515 | – 0,859 | 7,984 | – 0,053 | 1,550 |
| 2,949 | 7,234 | – 4,664 | – 5,911 | 5,145 |
| – 0,068 | – 0,537 | – 6,006 | 4,485 | – 8,707 |
| 2,628 | 4,714 | 2,998 | 1,386 | 8,213 |
| – 0,816 | 6,404 | 0,932 | 2,969 | 10,443 |
| 0,217 | – 4,986 | – 6,566 | 8,818 | – 1,711 |
| 7,268 | 5,486 | 1,118 | 2,369 | 1,961 |
| – 4,723 | 5,758 | 4,174 | 0,069 | – 1,913 |
| 5,097 | – 8,026 | – 6,561 | 2,185 | 3,561 |
7. Найти выборочное уравнение прямой 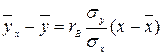регрессии y на x по данным корреляционной табл. 10.
Таблица 10
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 11
1. a)Известно, что в каждом испытании вероятность появления события А равна р = 0,3, n = 5, m = 3. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков равна 7, а разность равна 2.
c)В ящике 11 деталей, из которых 3 нестандартных. Наугад извлекают 3 детали. Найти вероятность того, что они стандартные.
d)В круг радиуса R =17 помещен правильный шестиугольник со стороной, равной 8. Найти вероятность того, что точка окажется внутри шестиугольника. Предполагается, что вероятность попадания точки в шестиугольник пропорциональна площади шестиугольника и не зависит от его расположения относительно круга.
e)Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,85, второй – 0,6. Найти вероятность того, что при аварии сработает только первый сигнализатор.
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x 1 с известной вероятностью р 1 = 0,2 и x 2, причем х 1 < х 2, М (X)=3,1 и D (X)=1,89.
3. Случайная величина Х задана функцией распределения
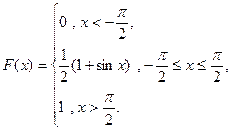
Найти: а) плотность вероятности f (x); б) M (x); в) D (x); г) σ (x); д) P (α < x < β), α = 0, β = 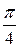. Построить графики F (x ) и f (x).
4. Случайная величина Х задана функцией плотности
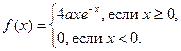
Найти: а) коэффициент а; б) F (x). Построить графики F (x) и f (x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β),если известны М (х) = m и σ (х) = σ; б) вероятность того, что | х – m | < δ, если α = 17, β = 22, m = 12, σ = 5, δ = 15.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М (х)и σ 2(х)по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
| 9,124 | – 6,854 | – 0,486 | 1,654 | 7,575 |
| 5,426 | – 1,143 | 4,540 | – 8,619 | – 2,464 |
| 7,777 | 2,844 | – 7,081 | – 8,951 | 7,265 |
| – 5,719 | – 12,467 | 0,353 | 7,070 | 4,650 |
| 8,867 | – 5,559 | – 2,458 | 2,948 | 1,212 |
| 9,339 | 0,096 | 11,929 | 6,291 | – 1,617 |
| 2,818 | – 3,021 | 2,788 | 8,652 | – 2,429 |
| – 9,894 | 12,284 | – 1,554 | 6,153 | 11,550 |
| 3,396 | – 6,039 | 8,357 | 2,293 | 11,454 |
| 4,175 | 8,715 | 13,870 | 0,112 | 0,042 |
7. Найти выборочное уравнение прямой 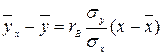регрессии y на x по данным корреляционной табл. 11.
Таблица 11
| x y | ny | ||||||
| nx | ∑=100 |
Вариант 12
1.a) Известно, что в каждом испытании вероятность появления события А равна р = 0,3, n = 5, m = 2. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков равна 8, а разность – 4.
c)Студент знает 13 из 20 экзаменационных вопросов. Ему предлагают ответить на 2 вопроса. Какова вероятность того, что он знает ответ на оба вопроса?
d)В круг радиуса R =9 помещен правильный шестиугольник со стороной, равной 5. Найти вероятность того, что точка окажется внутри шестиугольника. Предполагается, что вероятность попадания точки в шестиугольник пропорциональна площади шестиугольника и не зависит от его расположения относительно круга.
e) Вероятность попадания в цель при одном залпе для первого орудия равна 0,85, а для второго орудия – 0,95. Найти вероятность того, что при одном залпе в цель попадет только одно из орудий.
2. Найти закон распределения случайной вели
