П.1.2. Функциональное уравнение показательной функции

Покажем, что все непрерывные на всей действительной прямой функции, удовлетворяющие функциональному уравнению

f(x+y) = f(x) ·f(y), (5)

задаются формулой

f(x) = a^x (a>0)

(если не считать функции, тождественно равной 0).

Итак, пусть f(x) - непрерывная и определённая при всех действительных x функция, удовлетворяющая (5). Исключим тривиальное решение f(x) 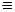0. Тогда для некоторого значения x = x₀ эта функция отлична от нуля. Положим в (5) y = x₀ - x:

f(x) ·f(x₀-x) = f(x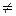₀) 0;

отсюда ясно, что f(x) не равна нулю ни при каком x. Заменяя x и y в (5) на x/2, получим

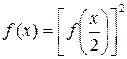
так что f(x) строго больше 0 для всех x. Тогда равенство (5) можно прологарифмировать, например, по основанию e:

ln f(x+y) = ln f(x) + ln f(y).

Положив в этом соотношении φ(x = ln f(x)), придём к функциональному уравнению Коши (4):

φ(x+y) = φ(x) + φ(y).

Учитывая, что φ - непрерывная функция (как суперпозиция непрерывных функций), имеем по доказанному:

φ(x) = ln f(x) = cx (c = const),

откуда находим, что

f(x) = e^ix = a^x (если положить a = e^c).

Таким образом, единственной непрерывной функцией, удовлетворяющей уравнению Коши (5), является показательная функция (или тождественно нулевая функция).

В качестве класса функций, в котором искалось решение (2), мы рассмотрели лишь класс непрерывных функций. Как и в предыдущем пункте, можно было бы разобрать решения для монотонных и ограниченных функций, но этого мы делать не будем, потому что (5), как было подмечено, сводится к (4), а для него всё ясно.