Определение:
Прямоугольной матрицей называется совокупность 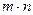 чисел, расположенных в виде прямоугольной таблицы, содержащей
чисел, расположенных в виде прямоугольной таблицы, содержащей 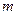 строк и
строк и  столбцов.
столбцов.
1.1. Основные действия над матрицами:
- сложение;
- разность;
- умножение матрицы на число;
- умножение матриц:
Если 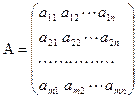 и
и 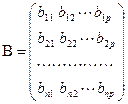 , то С = АВ
, то С = АВ 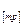 , где
, где
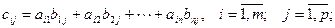
1.2. Элементарные преобразования матриц:
-перестановка двух любых столбцов (строк);
-умножение столбца (строки) на число отличное от нуля;
-прибавление к столбцу (строке) линейной комбинации других столбцов (строк);
1.3. Вычисление определителей:
Вычисление определители второго порядка
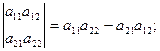
Вычисление определителей третьего порядка
а) по правилу треугольника
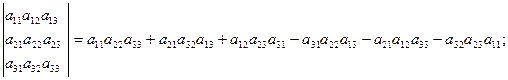
б) приведение к удобному виду;
в) разложение по элементам некоторого ряда.
1.4. Свойства определителей:
-величина определителя не изменится, если его транспонировать;
-перестановка двух любых параллельных рядов определителя равносильна его умножению на -1;
-если определитель имеет 2 одинаковых параллельных ряда, то он равен нулю;
-определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения;
|
|
|
-сумма произведений элементов какого-либо ряда на алгебраические дополнения элементов параллельного ряда равна нулю;
-если все элементы некоторого ряда содержат один и тот же множитель, то его можно вынести за знак определителя;
-если каждый элемент некоторого ряда определителя равен сумме двух слагаемых, то такой определитель можно представить в виде суммы 2 определителей, из которых один в рассматриваемом ряду имеет первые слагаемые, а другой вторые. На остальных местах у всех 3 определителей стоят одни и те же элементы;
-величина определителя не изменится, если к элементам некоторого ряда прибавить соответствующие элементы параллельного ряда, предварительно умножив их на один и тот же множитель;
-если все элементы некоторого ряда равны нулю, то сам определитель равен нулю;
-если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то определитель равен нулю;
1.5. Обратная матрица:
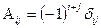 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 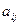 ;
; 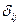 - минор элемента
- минор элемента 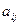 ( определитель 3- го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент);
( определитель 3- го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент);
Определение:
Матрица 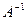 называется обратной квадратной матрице
называется обратной квадратной матрице  , если она, будучи умноженной как слева, так и справа на данную матрицу
, если она, будучи умноженной как слева, так и справа на данную матрицу  , дает соответствующую единичную, т.е.
, дает соответствующую единичную, т.е.
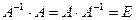
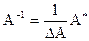 - формула вычисления обратной матрицы (
- формула вычисления обратной матрицы (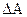 -определитель,
-определитель, 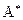 - матрица, составленная из алгебраических дополнений квадратной матрицы
- матрица, составленная из алгебраических дополнений квадратной матрицы  с последующим транспонированием);
с последующим транспонированием);
|
|
|
1.6.Свойства обратной матрицы:
- 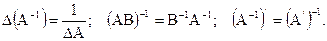
1.7. Формулы Крамера:
Пусть имеем систему  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными
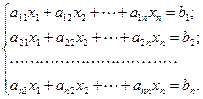 и пусть
и пусть 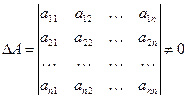 .
.
Система имеет единственное решение, которое можно найти по формулам Крамера:
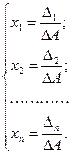 , где
, где 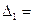
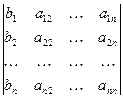 , ……,
, ……, 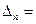
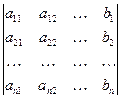
1.8. Теорема о числе решений совместных систем:
Пусть имеем совместную систему линейных уравнений
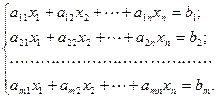
Так эта система совместна, то 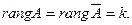 Назовем число k рангом совместной системы.
Назовем число k рангом совместной системы.
Теорема 1. Если ранг совместной системы равен числу неизвестных, то система имеет
единственное решение.
2.Если ранг совместной системы меньше числа неизвестных, то система имеет
бесчисленное множество решений.
Алгоритм решения совместных систем:
1) Пусть ранг совместной системы равен числу неизвестных и равен числу уравнений 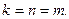 В этом случае единственное решение находят по формулам Крамера или матричным способом.
В этом случае единственное решение находят по формулам Крамера или матричным способом.
2) Пусть ранг совместной системы равен числу неизвестных, но меньше числа уравнений 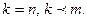 В этом случае необходимо в системе оставить лишь те уравнения, коэффициенты которых составляют базисный минор матрицы
В этом случае необходимо в системе оставить лишь те уравнения, коэффициенты которых составляют базисный минор матрицы  системы, а затем искать единственное решение либо по формулам Крамера, либо матричным способом.
системы, а затем искать единственное решение либо по формулам Крамера, либо матричным способом.
3) Пусть ранг совместной системы меньше числа неизвестных, 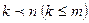 , тогда:
, тогда:
- в заданной системе выбираем 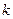 уравнений, из коэффициентов которых составлен базисный минор матрицы
уравнений, из коэффициентов которых составлен базисный минор матрицы  , а остальные уравнения отбрасываем;
, а остальные уравнения отбрасываем;
- неизвестные, коэффициенты при которых входят в базисный минор, так называемые главные неизвестные, оставляем в левой части системы, а остальные неизвестные, называемые свободными, переносим в правую часть;
- по формулам Крамера находим выражение главных неизвестных через свободные, полученные равенства представляют собой общее решение системы;
- придавая в общем решении свободным неизвестным конкретные числовые значения, находим конкретные числовые значения главных неизвестных. Совокупность числовых значений и главных, и свободных неизвестных дает определенное частное решение системы.
1.9.Однородные системы линейных уравнений:
Определение:
Систему линейных уравнений называют однородной, если все ее свободные члены равны нулю.
Теорема:
Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг системы меньше числа неизвестных.
Следствие:
Любая однородная система линейных уравнений, в которой число уравнений меньше числа неизвестных, имеет хотя бы одно нетривиальное решение.
Теорема:
Однородная система линейных уравнений, в которой число уравнений равно числу неизвестных, имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю.
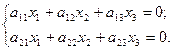 - однородная система двух уравнений с тремя неизвестными.
- однородная система двух уравнений с тремя неизвестными.
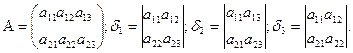
Ответ: 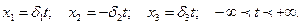
 2015-06-26
2015-06-26 1355
1355








